円と直線の問題を解くとき、定理を利用して計算することになります。そのため円と直線に関する定理を覚えていない場合、高校数学で問題を解くことができません。
円と直線の定理は複数あります。その中でも重要なのが「2つの接線の長さ」「接弦定理」「2つの円と直線の位置関係」です。これらの定理を利用することによって、辺の長さや角度を計算できるようになります。
円と直線の問題が出されることはよくあります。場合によっては、円と直線の関係についての証明問題も出されます。
それでは、どのように円と直線の定理を利用して問題を解けばいいのでしょうか。そこで、円と直線の関係性について解説していきます。
もくじ
円と直線の関係で重要な2つの定理
まず、一つの円を利用する場合について考えていきましょう。一つの円と直線の関係では、2つの重要な定理があります。以下になります。
- 円の外部から引く2つの接線の長さは同じになる
- 接弦定理:三角形の角度と接線が作る角度は同じ
それぞれの内容を確認していきましょう。
2つの接線の長さは同じになる
円の外部に一つの点を打ちましょう。この点をPとします。Pから円に接線を引くとき、二つの直線を引くことができます。直線と円の接点をそれぞれA、Bとするとき、APとBPの長さは同じです。
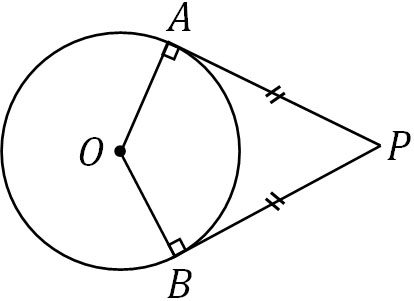
なぜ、AP=BPとなるのか理解するのはそこまで難しくないと思います。また、この定理を証明するのも簡単です。
まずAとBは接線であるため、円の中心Oからの距離は同じです。またAPとBPは接線なので、∠OAP=∠OBP=90°です。さらに、共通線なのでOPの長さは同じです。そのため直角三角形の合同条件より、斜辺と他の辺がそれぞれ等しいので△OAPと△OBPは合同です。
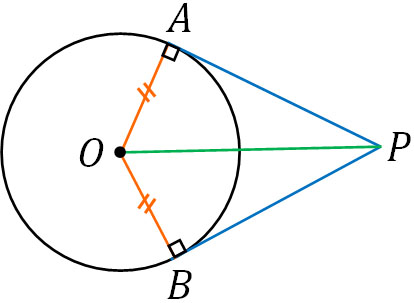
2つの三角形は合同であるため、AP=BPとなります。いずれにしても、円の外から2つの接線を引く場合、長さは同じになります。
接弦定理:三角形の角度と接線が作る角度は同じ
一つの円と直線の関係について、もう一つ重要な定理が接弦定理です。接弦定理では、三角形と接線について、以下の部分の角度が同じになります。
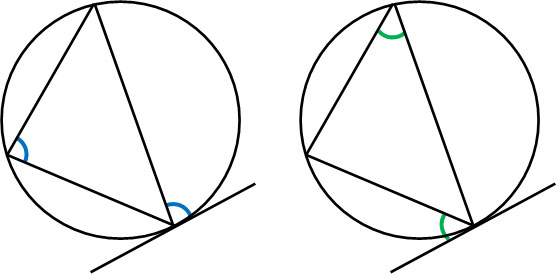
接弦定理を文章で表現するのは非常に難しいです。そこで、この位置関係を覚えましょう。
接弦定理についても証明するのは簡単です。円周角の定理を利用することによって接弦定理を証明できます。以下のように図を変えましょう。
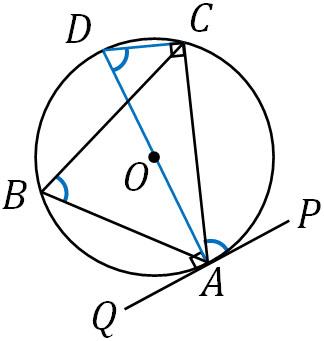
円周角の定理より、∠ABC=∠ADCです。△ADCに着目すると、ADは円の中心Oを通っているため、∠ACD=90°です。つまり、∠ADCは以下の式によって表されます。
- \(∠ADC=90°-∠CAD\) – ①
一方、PQは円の接線なので∠DAQ=90°です。そのため、∠CAPは以下の式によって表されます。
- \(∠CAP=90°-∠CAD\) – ②
①と②より、∠ADC=∠CAPであることを証明できました。接弦定理はひんぱんに利用される定理の一つなので、必ず覚えるようにしましょう。
二つの定理を利用して問題を解く
それでは、実際に問題を解いてみましょう。以下の答えは何でしょうか。
- 以下の図について、∠Cの大きさはいくらでしょうか。
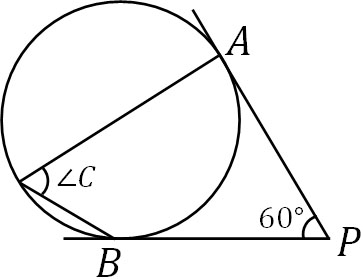
この問題を解くためには、先ほど解説した二つの定理を利用しましょう。以下のように図を作ることができます。
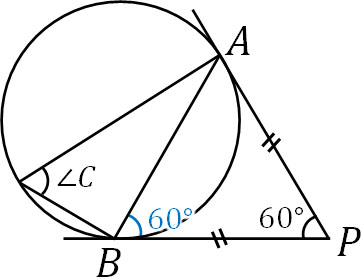
円の外から引いた接線の長さは等しいです。そのため、AP=BPです。△ABPは二等辺三角形であるため、一つの角度がわかればすべての角度がわかります。そこで計算すると、∠ABP=60°とわかります。
次に接弦定理を利用しましょう。∠ABP=60°なので、∠Cの大きさは60°です。こうして、∠Cの大きさを求めることができました。
接弦定理の逆を利用する
なお、場合によっては接弦定理の逆を利用することがあります。接弦定理の逆では、以下の部分の角度が等しい場合、APは円の接線です。
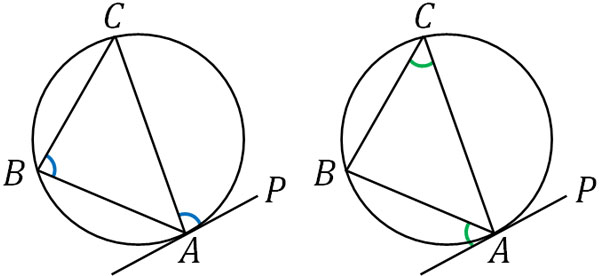
証明問題を解く場合、接弦定理の逆を利用することがあります。接線であることを証明したいとき、円と三角形が提示されているのであれば、接弦定理の逆を利用できるかどうか考えましょう。
円の半径と距離による2つの円の位置関係
それでは円が一つではなく、二つの場合はどのようになるのでしょうか。まず、二つの円と直線の関係について学びましょう。
二つの円について、半径をそれぞれm、nとします。二つの円の中心について、距離をdとすると、以下の関係が成り立ちます。
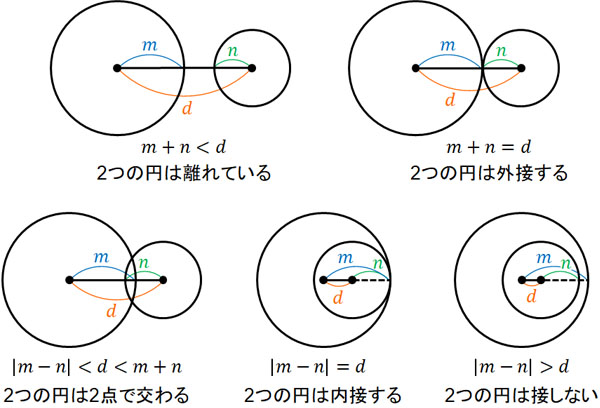
二つの円が提示されている場合、円の半径とそれぞれの円の中心との距離がどのような位置関係になっているのか確認する必要があります。
また、二つの円と接線の関係についても理解しましょう。二つの円の位置関係によって、接線の数が変化します。以下のようになります。
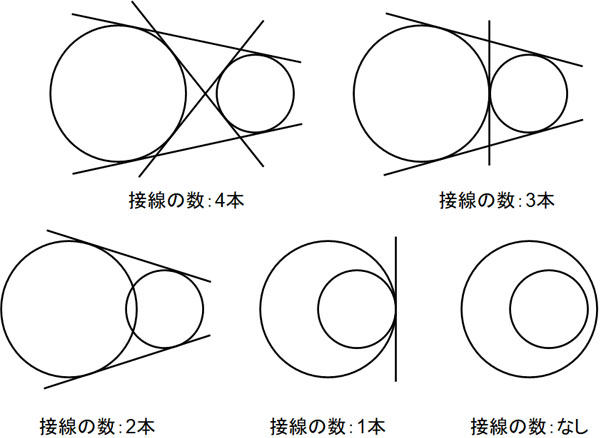
二つの円の位置によって接線の数が変わります。そこで、何本の接線を引けるのか確認しましょう。
二つの円と直線を利用する例題を解く
二つの円と直線が提示されている場合、先ほど解説したポイントをチェックしましょう。そうすると、問題を解けるようになります。例えば、以下の問題の答えは何でしょうか。
- 半径5の円と半径3の円があります。二つの円について、それぞれの中心との距離は8です。このとき、二つの円の接点と共通接線の接点を結ぶと直角三角形を作れることを示しましょう。
一つの円の半径が5であり、もう一方の円の半径が3なので、足すと8になります。またそれぞれの円の中心との距離が8なので、二つの円は外接することがわかります。そこで、以下の図を作りましょう。
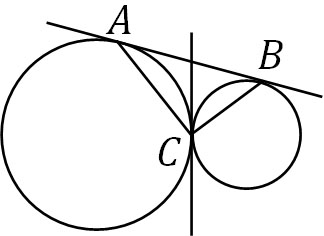
二つの円は外接するため、上図のような共通接線を引くことができます。そこで、3つの接点を結んだ△ABCが直角三角形であることを示しましょう。
まず、2本の接線の交点をDとします。前述の通り、円の外にある点から接線を引く場合、線の長さは等しいです。そのため、AD=DCです。また、同様にDB=DCです。つまり、AD=DB=DCとなります。
またAD=DB=DCより、3つの辺の長さが等しいため、点DはA、B、Cを通る円の中心であるとわかります。そのため、以下の図を作ることができます。
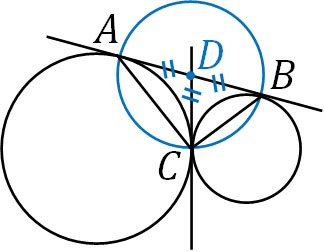
円周角の定理より、ABは円の中心Dを通るため、∠ACB=90°になります。こうして、△ABCが直角三角形であると証明することができました。
ここまで解説した知識を利用することによって図形の証明が可能になります。問題文からどのような図形なのかを読み解き、円と直線が関わる定理を利用して問題を解くようにしましょう。
円と直線が提示されたときに利用できる定理を覚える
数学で提示される問題では、定理を覚えていないと解けないケースがほとんどです。そこで、円と直線が関わる定理をすべて覚えましょう。
ここでは、「2つの接線の長さ」「接弦定理」「2つの円と直線の位置関係」について解説してきました。一つの定理を利用して解ける問題は少なく、多くのケースで複合問題となります。そこで、すべての定理を利用できるようになりましょう。
また図形の問題では証明問題もひんぱんに出されます。これらの定理を覚えていないと解けない証明問題は多いです。そこで辺の長さや角度の計算だけでなく、証明もできるようになりましょう。
図形の問題では適切に定理を利用できることが重要です。円と直線が提示されているとき、ここまで解説した定理を利用できるかどうか考えましょう。






