組み合わせ（C）の公式と順列・重複組み合わせの計算方法

確率の計算で重要な公式に組み合わせ（C: Combinations）があります。公式を利用しない場合、組み合わせの問題を解くのは難しいです。ただ公式を利用すれば、簡単に組み合わせの問題を解くことができます。

ただ組み合わせでは応用問題が頻繁に出されます。そこで条件が加えられるとき、どのように組み合わせの公式を利用すればいいのか理解しましょう。

また、組み合わせでは「同じものを含む順列」の計算をすることがあります。ほかには、同じ候補を何度選んでも問題ない組み合わせでは、重複組み合わせと呼ばれます。これらは問題の解き方を理解していないと答えを出すのが難しいです。

それでは、組み合わせの公式を利用してどのように問題を解けばいいのでしょうか。公式の利用方法や同じものを含む順列、重複組み合わせの計算方法を解説していきます。

1 順番を考慮しない場合が組み合わせ
2 同じものを含む順列の計算
- 2.1 同じものを含む順列には2通りの解答法がある
3 重複組み合わせの計算方法
- 3.1 必ず一つは選ばないといけない場合の重複組み合わせの解答方法
4 何通りの方法があるのか組み合わせの計算を行う

順番を考慮しない場合が組み合わせ

順列と組み合わせは計算方法が異なります。順列では順番が重要になります。順番を考慮するため、順列の公式を利用することで何通りの順番があるのか計算することができます。

一方で組み合わせでは、順番を考慮しません。並べる順番を無視して選ぶとき、何通りの方法があるのか数えるのが組み合わせです。例えば、以下のようになります。

・カードを選ぶ

順列：7枚のカードから3枚を選び、3ケタの数字を作る（左から順に並べる）
組み合わせ：7枚のカードから3枚を選ぶ

・代表者の決定

10人の中から、リーダーと副リーダーを決める
10人の中から、2人のリーダーを決める

カードを左から順に並べるとき、順列を利用します。一方でカードを選ぶものの、順番を考慮しない場合は組み合わせを利用します。

また代表者を決定するとき、リーダーと副リーダーは明確に区別できます。またリーダーと副リーダーを選ぶというのは、「リーダーと副リーダーの順に並べる」ことと意味が同じです。そのため順列を利用します。ただ2人のリーダーについては、両者を区別できません。そのため組み合わせを利用します。

このように、順番を考慮するのかしないのかによって順列と組み合わせを使い分けるようにしましょう。

組み合わせの公式と計算方法

それでは、組み合わせではどのように計算すればいいのでしょうか。例えば6枚のカードから3枚を選び、左から順に並べる場合、₆P₃と表します。

\(_6P_3=6×5×4=120\)

一方で左から順に並べず、6枚のカードから3枚を選ぶとき、何通りの方法があるでしょうか。組み合わせを利用する場合、PをCに変えましょう。そのため6枚のカードから3枚を選ぶ場合、₆C₃と表します。

n個の中からr個を取る場合、_nC_rと表されます。組み合わせの記号を利用するとき、PをCに変えるだけです。

・組み合わせの公式を利用する

次に組み合わせの公式を利用して計算できるようになりましょう。₆C₃はどのように計算すればいいのでしょうか。組み合わせの公式では分数を利用します。n個の中から選ぶ場合、分子にはn!を置きましょう。また分母では、\(r!\)と\((n-r)!\)のかけ算をします。

そのため、以下のような公式になります。

\(_nC_r=\displaystyle\frac{n!}{r!(n-r)!}\)

公式を見るよりも、実際の計算を確認するほうが理解しやすいです。例えば、以下のようになります。

\(_5C_2=\displaystyle\frac{5!}{2!(5-2)!}=\displaystyle\frac{5!}{2!3!}\)
\(_{10}C_7=\displaystyle\frac{10!}{7!(10-7)!}=\displaystyle\frac{10!}{7!3!}\)
\(_8C_6=\displaystyle\frac{8!}{6!(8-6)!}=\displaystyle\frac{8!}{6!2!}\)
\(_{100}C_{78}=\displaystyle\frac{100!}{78!(100-78)!}=\displaystyle\frac{100!}{78!22!}\)

このように、Cの左と右にある数字を確認して計算式を作ります。この公式は組み合わせの計算で頻繁に使うことになるため、必ず覚えるようにしましょう。

なお6枚のカードから3枚を選ぶとき、組み合わせの公式を利用すると、前に示したように₆C₃となります。これを計算すると以下のようになります。

\(_6C_3=\displaystyle\frac{6!}{3!3!}=\displaystyle\frac{6×5×4×3×2}{3×2×3×2}=20\)

こうして、20通りが答えとわかります。

なお組み合わせでは、_nC₀＝_nC_n＝1となります。例えば、₇C₀＝₇C₇＝1です。7個の中から何も選ばない場合、方法は1通りです。また7個の中からすべて選ぶ場合、方法は1通りです。そのため、_nC₀＝_nC_n＝1になると理解しましょう。

また公式を理解すれば、例えば₇C₂と₇C₅は同じ答えになるとわかります。以下の計算式になるからです。

\(_7C_2=\displaystyle\frac{7!}{2!(7-2)!}=\displaystyle\frac{7!}{2!5!}\)
\(_7C_5=\displaystyle\frac{7!}{5!(7-5)!}=\displaystyle\frac{7!}{5!2!}\)

このように、同じ計算式になります。

先に約分をして、組み合わせの計算を早くする

先ほど、組み合わせの公式を利用する方法を解説しました。ただ計算をするとき、できるだけ計算が簡単であるほどいいです。そこで順列の公式を利用することによって、組み合わせの計算を素早くしましょう。

具体的には、\(r!\)と\((n-r)!\)を比較して、数字の大きいほうと分子を事前に約分します。そうすると、計算が簡単になります。

例えば、以下のようになります。

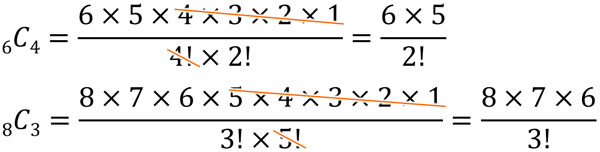
慣れていない場合、組み合わせの公式を利用して計算するようにしましょう。一方で組み合わせの計算に慣れた場合、素早く計算するため、先に約分をして分数を簡略化しましょう。

組み合わせで重要な組み分け（グループの区別）の問題

なお組み合わせの問題を解くとき、組み分けの問題が頻繁に出されます。つまりグループへ分けるとき、区別できるかどうか確認しなければいけません。

どのように答えを出すのかについて、以下の例題を解いてみましょう。

12人を以下のようにわけるとき、何通りの方法がありますか？

5人、4人、3人に分ける
4人ずつA、B、Cのグループに分ける
4人ずつ、3つのグループに分ける
6人、3人、3人のグループに分ける

(a) 5人、4人、3人に分ける

人をグループ分けするとき、順番を気にせずにグループへ入れます。そのため、組み合わせの公式を利用します。最初、12人から5人を選ぶので₁₂C₅です。次に残った7人から4人を選ぶので₇C₄です。なお、最後は3人の中から3人を選ぶので₃C₃です。ただ、₃C₃は1なので計算を省きます。

そのため、以下の計算式を作ることができます。

\(_{12}C_5×_7C_4=\displaystyle\frac{12!}{5!7!}×\displaystyle\frac{7!}{4!3!}=27720\)

組み合わせの公式を利用することによって、27720通りの方法があるとわかります。

(b) 4人ずつA、B、Cのグループに分ける

次に、4人ずつA、B、Cのグループに分ける場合を考えてみましょう。考え方は先ほどと同じです。最初、12人から4人を選ぶので₁₂C₄です。次に、8人の中から4人を選ぶので₈C₄です。そのため計算式は以下です。

\(_{12}C_4×_8C_4=\displaystyle\frac{12!}{4!8!}×\displaystyle\frac{8!}{4!4!}=34650\)

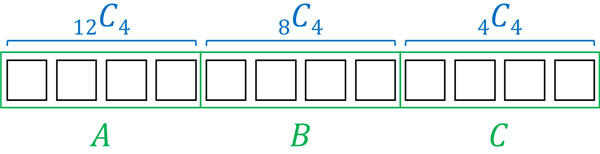
(c) 4人ずつ、3つのグループに分ける

4人ずつ3つのグループに分けるものの、Aグループ、Bグループ、C、グループなどの区別がないケースでの組み合わせです。この場合、先ほどの計算とは少しやり方が異なります。A、B、Cの区別をなくす場合、グループの分け方は3!通りあります。

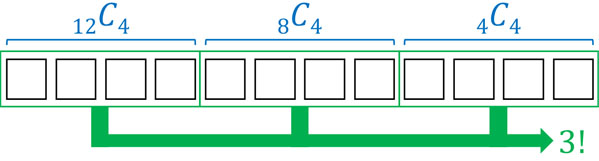
そこで3!通りの区別をなくすため、(b)の結果に対して3!で割りましょう。

\(\displaystyle\frac{34650}{3!}=5775\)

(a)の計算では、グループの分け方を考慮せずに₁₂C₅×₇C₄の計算をしました。この理由としては5人、4人、3人に分けるからです。5人、4人、3人のグループであれば、Aグループ、Bグループ、Cグループと区別しなくても、それぞれのグループを見分けることができます。

一方ですべてのグループが4人の場合、Aグループ、Bグループ、Cグループのように区別しないと、私たちは見分けることができません。例えば12人を以下のように分けるとき、以下はすべて同じ結果と考えることができます。

(1-2-3-4), (5-6-7-8), (9-10-11-12)
(5-6-7-8), (1-2-3-4), (9-10-11-12)
(9-10-11-12), (5-6-7-8), (1-2-3-4)

(c)の計算ではグループを区別しないため、その分を考慮して3!で割り算をします。

(d) 6人、3人、3人のグループに分ける

それでは、6人、3人、3人のグループに分ける場面を考えてみましょう。12人から6人を選ぶため式は₁₂C₆です。次に6人から3人を選ぶので式は₆C₃です。

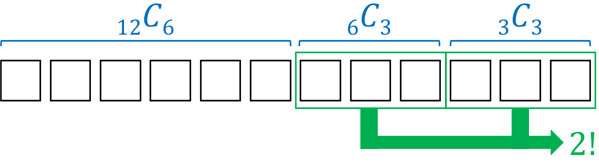
ただ、3人のグループが2つあります。6人グループと3人グループについては、私たちは見分けることができます。ただ、2つの3人グループは見分けることができません。そこで、3人グループの区別をなくすために2!で割りましょう。

\(\displaystyle\frac{_{12}C_6×_6C_3}{2!}=9240\)

このように、区別できないグループについてはわり算をすることで何通りのケースがあるのか計算できます。

同じものを含む順列の計算

次に、同じものを含む順列の計算をしてみましょう。先ほど説明した練習問題を解ける場合、同じものを含む順列の計算は簡単です。

一般的な順列では、左から順に並べるとき、すべての要素を見分けることができます。そのため階乗や順列の公式を利用することによって答えを出すことができます。一方、以下の8個のように宝石を並べるとき、どのように考えればいいでしょうか（同じ色の宝石は見分けることができないとする）。

色が違う場合、宝石を見分けることができます。ただ色が同じ宝石については、私たちは見分けることができません。

先ほど、区別できない要素については、割り算をすることによって結果から省かなければいけないことを解説しました。今回の計算についても、同じものについて割り算をすることによって省くようにしましょう。

8個の宝石を左から順に並べるとき、8!通りの方法があります。その後、見分けることができない要素を割り算しましょう。以下のように考えます。

\(\displaystyle\frac{8!}{2!2!3!1!}=1680\)

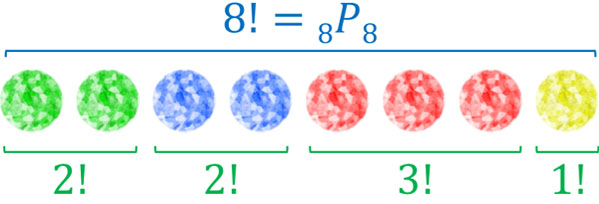
このように、見分けることができない要素について順列を計算し、割り算をします。これによって、同じものを含む順列を計算できます。

同じものを含む順列には2通りの解答法がある

なお、同じものを含む順列には他にも解答方法があります。そこで、次は組み合わせの公式を利用して先ほどの問題を解いてみましょう。

宝石を8個並べるとき、同じ色を区別することができません。そのため、例えば緑の宝石を置くとき、「8個の中から2個を選べばいい」と考えることができます。そのため式は₈C₂です。

次に青の宝石を置くとき、残りの6個の中から2個を選ぶので式は₆C₂です。また赤色の宝石を置くとき、残りの4個の中から3個を選ぶので₄C₃です。

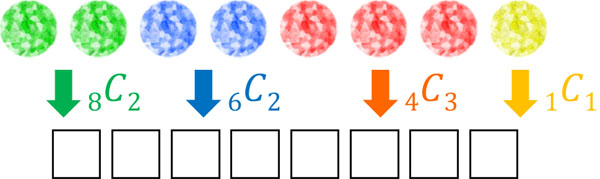
そこで、以下の計算をしましょう。

\(_8C_2×_6C_2×_4C_3=1680\)

こうして、先ほどと同じ答えを出すことができます。どちらの方法も正解であり、同じものを含む順列では2通りの解き方があります。

重複組み合わせの計算方法

組み合わせの問題では、「何度も同じ要素を利用できる組み合わせ」があります。通常、組み合わせでは一回だけ選ぶことができます。例えば、8人の中から4人を選ぶとき、計算式は₈C₄です。分身できる場合を除き、同じ人間を一度に二回選ぶことはできません。

ただ物を選ぶときであれば、同じものを重複して選べるケースがあります。例えば、以下の状況を考えてみましょう。

みかん、リンゴ、バナナについて、合計8個を買うとき、何通りの方法がありますか（一つも買わない果物があってもいい）

例えばみかんを6個買う場合、同じもの（みかん）を重複して6個買うことになります。リンゴを2個買う場合、同じもの（リンゴ）を重複して2個買うことになります。みかんやリンゴ、バナナが店にたくさん置かれている場合、何個でも買うことができるのです。

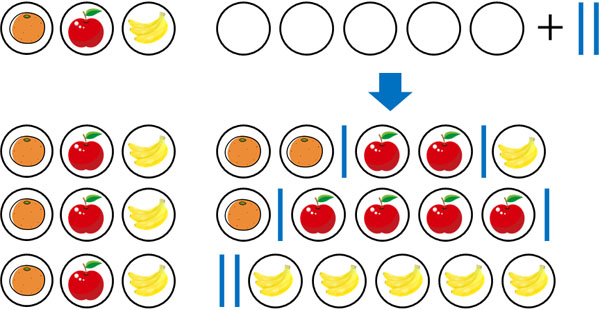
なお重複組み合わせの問題を解く場合、考え方が特殊です。具体的には、区切り（|）を利用して問題を解きましょう。先ほどの問題であれば、合計で8個の果物を買います。そこで、以下のように8個の〇を作りましょう。

次に、仕切りを2つ加えます。仕切りが2つあれば、以下のように区切る場所によってみかん、リンゴ、バナナを買う個数を分けることができます。

丸は8つであり、仕切りは2個です。そのため「10個の場所から、2ヶ所の仕切りを置く場所を選べばいい」と考えることができます。つまり、計算式は以下になります。

\(_{10}C_2=45\)

重複組み合わせの考え方は特殊であり、解き方を理解していないと答えを出すことができません。なお先ほどの問題について、4種類の果物（みかん、リンゴ、バナナ、ぶどう）を合計8個買うときでは、〇が8つであり、仕切りが3つ必要になるので以下の計算式になります。

\(_{11}C_3=165\)

3つに分ける場合、仕切りは2つ必要です。また4つに分ける場合、仕切りは3つ必要です。分ける数から1を引くと、必要な仕切りの数になります。

なお重複組み合わせでは、n個から重複を許してr個を取り出す場合、以下の公式があります。

\(_nH_r=_{n+r-1}C_r\)

この公式を覚えてもいいですが、意味を理解していないと利用することができません。そこで、丸と仕切りを利用することによって重複組み合わせの答えを出すようにしましょう。

必ず一つは選ばないといけない場合の重複組み合わせの解答方法

先ほど、一つも選ばない果物があっても問題ないケースで重複組み合わせを考えました。それでは、以下のケースではどのように考えればいいでしょうか。

みかん、リンゴ、バナナについて、合計8個を買うとき、何通りの方法がありますか（どの果物も少なくとも1個は買う）

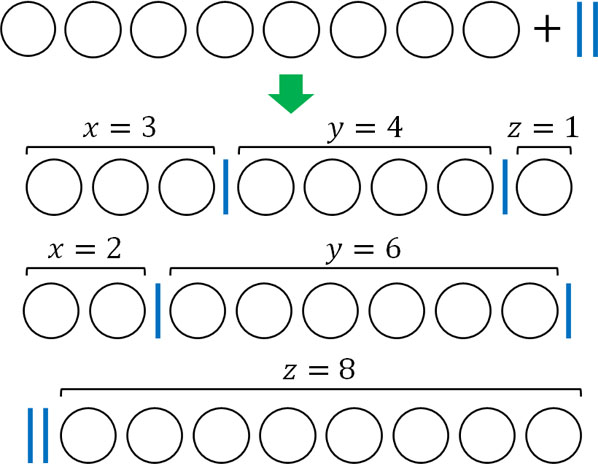
この場合も同じように、区切りを利用して問題を解きます。必要な区切りは2つです。ただ少なくとも、みかん1個、リンゴ1個、バナナ1個は必ず買わなければいけません。8個を買う中で、3個はすでに決まっています。そのため、この3つについては除外しましょう。

そうして残った5つについて、仕切り2つを利用して以下のように分けることができます。

選ぶ候補が5つ、仕切りが2つであるため、以下の計算式になります。

\(_7C_2=21\)

1つ以上を選ぶ重複順列では、何個を先に選ぶのかによって引き算をする数を決めましょう。今回では、買う合計数（8個）のうち3個（ミカン1個、リンゴ1個、バナナ1個）を買うと既に決まっているため、3を引きます。

そのため、例えば4個（少なくともミカン2個、リンゴ1個、バナナ1個）を買うと既に決まっている場合、4を引きます。つまり選べる候補は4つであり、仕切りは2つになります。

そのため、以下の計算式になります。

\(_6C_2=15\)

仕切りを利用すれば、重複組み合わせの答えを得ることができます。例えば、以下の答えは何でしょうか。

\(x+y+z=8\)であり、\(x≧0\), \(y≧0\), \(z≧0\)の整数について、\(x,y,z\)の組み合わせは何通りでしょうか

\(x\)や\(y\)、\(z\)は何度選んでもいいです。そのため重複組み合わせであり、以下のように2つの仕切りを利用しましょう。

こうして、以下の計算をすることができます。

\(_{10}C_2=45\)

一方、以下の答えは何でしょうか。

\(x+y+z=8\)であり、\(x,y,z\)が自然数のとき、\(x,y,z\)の組み合わせは何通りでしょうか

\(x,y,z\)は自然数なので、必ず\(x≧1\),\(y≧1\),\(z≧1\)となります。そこで、3つ分を除外して組み合わせを考えましょう。以下のようになります。

\(_7C_2=21\)

問題文は異なるものの、考え方や計算方法は同じです。重複組み合わせを計算するとき、仕切りを利用することによって答えを出しましょう。

何通りの方法があるのか組み合わせの計算を行う

小学算数などで行う組み合わせの計算は非常に難しいです。公式なしに何通りの方法があるのか計算しなければいけないからです。一方で組み合わせの公式を学ぶ場合、非常に計算が簡単になります。そこで、組み合わせの公式を利用して計算しましょう。

なお組み合わせの計算では、分けた後にグループを区別できるかどうかによって答えが変わります。そのため答えを出した後、区別できるグループかどうか確認しましょう。

またこの考え方を理解すれば、同じものを含む順列の計算ができるようになります。区別できないものが含まれている場合、区別できない要素について何通りの方法があるのか計算し、割り算をしましょう。

他には、重複組み合わせの問題が出されることもあります。この場合は仕切りを利用することになるため、解き方を理解しましょう。ここまでの内容を学べば、あらゆる組み合わせの問題を解けるようになります。