数学で学ぶ分野の一つが集合と要素です。どのような要素が含まれているのか表すのが集合です。数学では、特定の要素が含まれているかどうかを考えます。
また数学では、一つの集合を考えるのではなく、2つや3つの集合を考えます。2つの集合について、共通部分や共通しない部分を探すのです。
集合と要素は日常生活で頻繁に利用されます。そのため数学での考え方を理解していれば、どのように要素を考えればいいのかわかるようになります。数字を利用しない場合であっても、集合の考え方は有効なのです。
それでは、どのように集合を理解すればいいのでしょうか。集合の概念やその否定、ド・モルガンの法則など、基本的な考え方を解説していきます。
もくじ
集合と要素の表し方
まず、集合とは何かを理解しましょう。明確にわかっているものの集まりが集合です。例えば1~9の数字を集合Aとすると、Aは以下のように表されます。
- A{1, 2, 3, 4, 5, 6, 7, 8, 9}
このように、数字をすべて書くことによって集合を表すことができます。また、集合を構成しているものを要素といいます。今回の場合、1~9の数字が要素です。
重要なポイントとして、要素をすべて書かない方法であっても集合を表すことができます。例えば、以下のように記してもいいです。
- A{n | nは整数, 1≦n≦9 }
nについて縦線(|)で区切り、右側にnの条件を記していきます。nが整数であり、かつ1≦n≦9を満たす数字は1~9です。このように、明確にわかっている要素の集まりが集合です。
集合によっては、数が無限に続いていくことがあります。例えば集合Bとして、偶数の集合を表したい場合、一つずつ要素を記すことはできません。偶数は無限に数が続いていくため、すべての要素を記すことができません。そこで、以下のように集合Bを表します。
- B{2n | nは整数}
このようにすれば偶数を表現できます。nが整数であり、かつ2nの数字は必ず偶数になります。
要素が集合に含まれる場合の表現
次に、「要素が集合に含まれているか」どうかに関する記号を学びましょう。先ほどと同じように、1~9の数を含む集合Aがあるとします。
- A{1, 2, 3, 4, 5, 6, 7, 8, 9}
4という数字は集合Aに含まれます。この場合、\(∈\)または\(∋\)という記号を利用して次のように表現されます。
- \(4∈A\)(または\(A∋4\))
4\(∈\)Aというは、「4はAに属する」という意味になります。考え方は簡単であるものの、記号の意味を知らない場合、何を表しているのか理解できません。
一方、10という数字は集合Aに含まれません。この場合、\(∉\)または\(∌\)という記号を利用して次のように表現されます。
- \(10∉A\)(または\(A∌10\))
\(10∉A\)というのは、「10はAに属さない」ことを意味します。記号を利用することによって、要素が集合に含まれるのかどうかを表すことができます。
部分集合と空集合の関係
なお集合では、2つまたは3つの集合を比較します。そこで集合を図で表すとき、どのように図を作ればいいのか学びましょう。1~9の整数を含む集合Aであれば、以下のように表すことができます。

このような図をベン図といいます。それでは、B{2, 4, 6, 8}の集合はどのようなベン図で表せばいいでしょうか。集合Aと集合Bを比べると、集合Bは集合Aに含まれていることがわかります。そのため、以下のようなベン図を作ることができます。
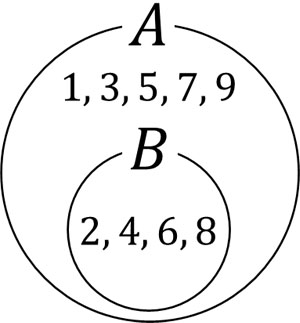
BはAの要素でもあります。この場合、「BはAの部分集合」と表現されます。また、\(⊂\)または\(⊃\)という記号を利用することによって部分集合であることを表すことができます。以下のようになります。
- \(B⊂A\)(または\(A⊃B\))
AがBをつかみにいくイメージをもちましょう。そうすれば、B\(⊂\)Aが何を表しているのか理解しやすくなります。
・空集合(Φ)の意味
ただ場合によっては、要素が存在しないケースがあります。数字で0があることからわかる通り、要素をもたない集合があることを理解しましょう。こうした集合を空集合といいます。通常、空集合はギリシャ文字のΦ(ファイ)を利用して表現します。
例えば、負の数である自然数には何があるでしょうか。1以上の正の整数が自然数です。そのため、負の数である自然数はありません。この場合、要素が存在しないので空集合となります。
共通部分と和集合の表し方
次に共通部分と和集合を理解しましょう。2つの集合を比べるとき、同じ要素をもっているケースがあります。同じ要素については共通部分といいます。例えば、以下の集合Aと集合Bの共通部分は何でしょうか。
- A{1, 2, 3, 4}
- B{3, 4, 5, 6, 7}
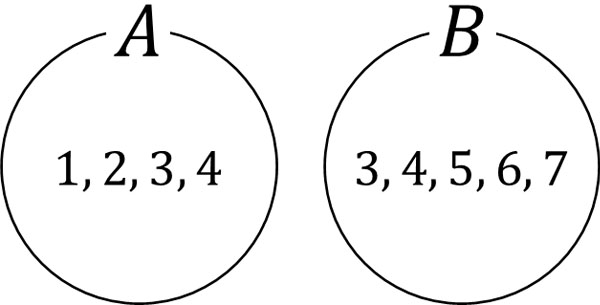
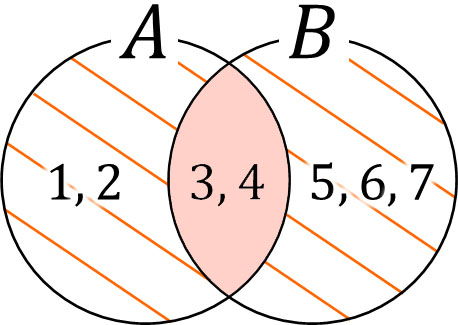
2つの集合を確認すると、共通部分は3と4であることがわかります。ベン図にすると以下のようになります。
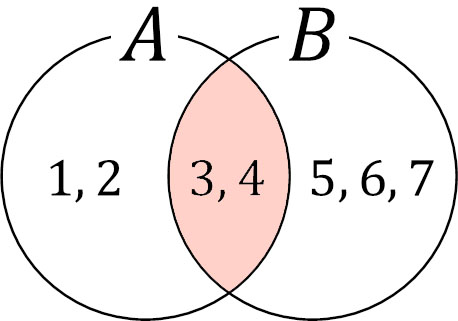
2つの集合の共通部分について、数学では\(∩\)という記号を利用してA\(∩\)Bと表現します。今回の場合、AかつBの要素は3と4です。そのため、以下のようになります。
- \(A∩B\)={3, 4}
・和集合は\(∪\)の記号を使う
AかつBを表すのがA\(∩\)Bです。一方、AまたはBを表すときはどのようにすればいいのでしょうか。AまたはBであるため、AとBの両方の要素を含むことになります。こうした集合を和集合といいます。
そこで、以下のAとBの和集合をベン図にして考えてみましょう。
- A{1, 2, 3, 4}
- B{3, 4, 5, 6, 7}
AまたはBの集合を表すとき、\(∪\)という記号を使ってA\(∪\)Bと表現します。AとBの要素をすべて足すと以下のようになります。
- \(A∪B\)={1, 2, 3, 4, 5, 6, 7}
考え方は難しくないものの、記号の意味を覚える必要があります。おさらいすると、以下のようになります。
- \(A∩B\)=AかつB
- \(A∪B\)=AまたはB
\(∩\)が共通部分を意味し、\(∪\)が和集合を意味することを理解しましょう。
・3つの集合を考える
次に、3つの集合について共通部分と和集合を考えてみましょう。以下の集合A、集合B、集合Cがあるとします。
- A={\(x\) | \(x\)は10以下の正の奇数}
- B={\(x\) | \(x\)は15の約数}
- C={\(x\) | \(x\)は3の倍数であり、\(1≦x≦12\)}
このとき、\((A∪B)∩C\)となる要素は何でしょうか。それぞれの要素を書き出すと以下のようになります。
- A={\(x\) | 1, 3, 5, 7, 9}
- B={\(x\) | 1, 3, 5, 15}
- C={\(x\) | 3, 6, 9, 12}
次に、ベン図にしてみましょう。以下のようになります。
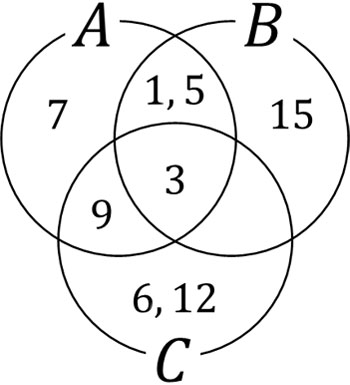
\(A∪B\)となる要素は以下のようになります。
- \(A∪B\)={\(x\) | 1, 3, 5, 7, 9, 15}
そのため、\((A∪B)∩C\)は以下のようになります。
- \((A∪B)∩C\)={\(x\) | 3, 9}
集合にどのような要素があるのか記したり、ベン図を利用したりすることによって、答えを見つけることができます。
全体集合と補集合とは何か
次に全体集合を学びましょう。集合を利用するとき、最初に集合を作り、そのあとに部分集合を利用するのが普通です。例えば製品を作るとき、不良品が作られることがあります。つまり、以下のようになります。
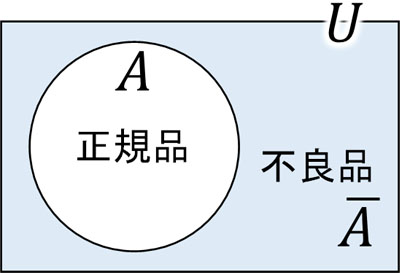
この場合、全体の要素を全体集合といいます。今回の場合であれば、作られる製品すべてが全体集合です。全体集合はUを利用することで表します。全体を表すため、全体集合は必ず正規品である集合Aを含みます。
- \(A⊂U\)
一方、前述のとおり不良品が作られることもあります。不良品は全体集合(U)の要素であるものの、A以外の要素です。この場合、不良品の部分を\(\overline{A}\)と表します。\(\overline{A}\)というのは、A以外の要素を意味します。
また、特定の要素以外を補集合といいます。例えば、\(\overline{A}\)はAの補集合です。また補集合については\(A∪\overline{A}=U\)と\(A∩\overline{A}=Φ\)が成り立ちます。ベン図を描けばこの理由がわかります。
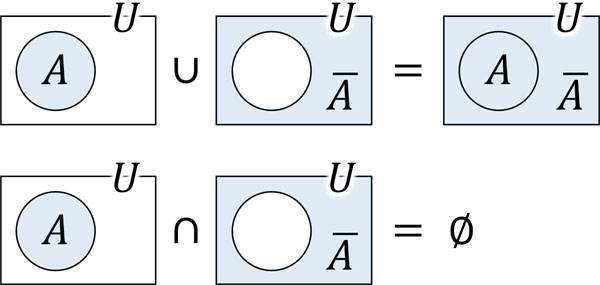
集合では、数字をみても理由を理解するのは難しいです。しかしベン図を利用すれば、理由を簡単に理解できるようになります。
補集合ではド・モルガンの法則が成り立つ
なお集合では、ド・モルガンの法則を理解するようにしましょう。ド・モルガンの法則では以下の条件が成り立ちます。
- \(\overline{A∪B}=\overline{A}∩\overline{B}\)
- \(\overline{A∩B}=\overline{A}∪\overline{B}\)
この理由についても、ベン図を利用すれば理解しやすいです。以下のようになります。
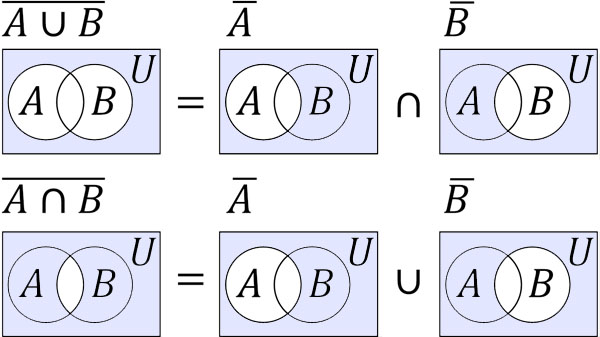
このように\(\overline{A}\)や\(\overline{B}\)が何を表すのか図にすることによって、なぜド・モルガンの法則が成り立つのか理解できるようになります。
次に、例題を解いてみましょう。U={1, 2, 3, 4, 5, 6, 7, 8, 9}の全体集合があり、部分集合としてAとBがあるとします。\(\overline{A}∩\overline{B}\)={1, 4, 6}の場合、AにもBにも属さない要素は何でしょうか。
以下のように、AにもBにも属さない要素は\(\overline{A∪B}\)と表すことができます。
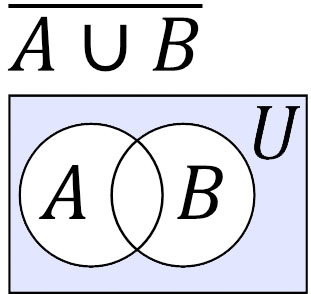
ド・モルガンの法則より、\(\overline{A}∩\overline{B}=\overline{A∪B}\)です。そのため、\(\overline{A∪B}\)={1, 4, 6}が答えです。このように、ド・モルガンの法則を利用することによって問題を解くことができます。
集合で学ぶ言葉を理解する
集合と要素を学ぶとき、苦手とする人は多いです。この理由として、新たな言葉や記号を覚える必要があるからです。集合と要素では、記号の意味を理解していなければ問題を解くことができません。
ただ概念は難しくなく、ベン図を利用すれば解ける問題がほとんどです。言葉や記号の意味を覚える必要はあるものの、集合にどのような要素が含まれているのか一つずつ書き出すようにしましょう。そうすれば、答えを出すことができます。
また集合の問題では、2つ(または3つ)の集合を比較する問題がほとんどです。そこで全体集合や補集合の考え方を利用して、集合に含まれる要素を探しましょう。場合によっては、ド・モルガンの法則を利用しなければいけないこともあります。
まずは言葉と記号の意味を覚えましょう。その後、集合に含まれる要素を見つけられるようにしましょう。