平方根の掛け算・割り算：ルート計算と素因数分解のやり方

平方根では掛け算と割り算を学びます。一般的に数学では、最初に足し算と引き算を学びます。ただ平方根については、掛け算と割り算のほうが簡単です。根号（ルート）の数字をそのまま掛け算すればいいからです。

ただ、平方根の掛け算にはルールがあります。また、なぜルート同士の掛け算をしてもいいのか理解している人は少ないです。平方根の掛け算と割り算について、なぜそうなるのか理由を含めて学ばなければいけません。

また平方根ならではの計算方法が存在します。それが素因数分解です。素因数分解をすることで計算が簡単になり、正しい答えを出すことができます。平方根の掛け算と割り算では、同時に素因数分解を学ばなければいけません。

ルート計算の掛け算では、新たな概念を学ぶ必要があります。どのように平方根の掛け算・割り算をすればいいのか解説していきます。

平方根の掛け算・割り算の方法

平方根では前述の通り、足し算と引き算の前に掛け算・割り算を学びます。なぜ、平方根では掛け算を先に学ぶのでしょうか。それは、平方根同士の掛け算はやり方が簡単だからです。ルート内の数字は掛け算が可能です。

根号（ルート）の掛け算では、以下の公式になります。

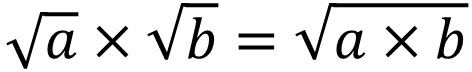
そのため、例えば以下のような計算になります。

• $\sqrt{2}×\sqrt{3}=\sqrt{6}$
• $\sqrt{7}×\sqrt{11}=\sqrt{77}$

また、割り算は掛け算と同じです。割り算は分数の掛け算に直すことができるからです。ルート同士の掛け算が可能なため、ルート内の数字も同じように割り算できます。

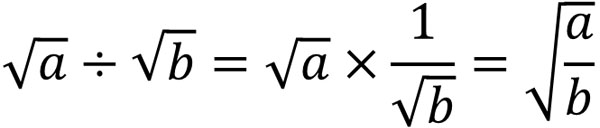
そのため、以下のように割り算を計算します。

• $\sqrt{21}÷\sqrt{3}=\sqrt{7}$
• $\sqrt{15}÷\sqrt{5}=\sqrt{3}$

ルート同士の掛け算・割り算では、通常の掛け算・割り算をすればいいです。違うのはルートがあるかどうかだけです。

整数と平方根は別々に掛け算・割り算をする

ただ重要なのは、整数と平方根を分けて掛け算または割り算をすることです。整数と平方根はまったく別の数字だからです。

ルートでは$3\sqrt{2}$などの記載されることがあります。これは3と$\sqrt{2}$の掛け算であり、$3×\sqrt{2}$と意味は同じです。ただ$×$を省略するのが基本なので、$3\sqrt{2}$と記されます。

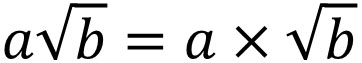
ルートの前にある数字（整数）を分けて考えるため、整数とルートは別々に掛け算をしましょう。つまり、以下のようになります。

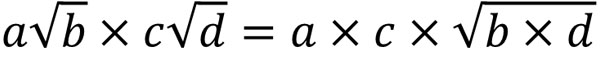
整数は整数と掛け算をします。一方でルートはルートと掛け算をします。整数とルートの掛け算をすることはありません。掛け算と割り算では、整数とルートを完全に分けて計算しましょう。

そのため、例えば以下のようになります。

• $3×\sqrt{2}=3\sqrt{2}$
• $2×4\sqrt{2}=8\sqrt{2}$
• $2\sqrt{2}×3\sqrt{5}=6\sqrt{10}$

このように、整数と根号（ルート）を分けて計算しています。

ただ、整数はルートに直すことができます。2乗させれば、整数をルートに変換できます。例えば、$2=\sqrt{2^2}=\sqrt{4}$です。同じように考えると、$3=\sqrt{9}$です。また、$4=\sqrt{16}$です。

整数とルートの掛け算や割り算はできません。そこで整数をルートに直せば、ルート同士の掛け算と割り算が可能になります。例えば、以下の問題はどのように解けばいいでしょうか。

• $\displaystyle\frac{\sqrt{12}}{2}$

$\sqrt{12}$と2は掛け算・割り算ができません。そこで、根号（ルート）を使って2を表しましょう。$2=\sqrt{4}$なので、以下のように計算できます。

• $\displaystyle\frac{\sqrt{12}}{2}=\displaystyle\frac{\sqrt{12}}{\sqrt{4}}=\sqrt{3}$

整数とルートは掛け算できません。ただ、整数はルートに直すことができます。そのためより正確にいうと、整数をルートに変換することで、整数とルートの掛け算・割り算が可能になります。

ルート同士の掛け算・割り算が可能な理由

それでは、なぜルート同士の掛け算・割り算が可能なのでしょうか。この理由について、理解している人は少ないです。

この理由を理解するためには、一次方程式を使います。方程式には、両辺に同じ数を掛けても問題ないという性質があります。例えば、以下のてんびんがあるとします。

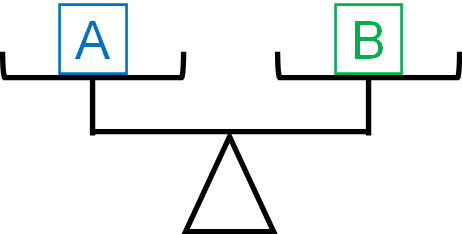
2つが同じ場合、両辺を何倍してもイコールは成り立ちます。

なぜ根号（ルート）の掛け算が成立するのか理解するためには、方程式の性質をおさらいしましょう。

・ルートの掛け算が成り立つ理由を証明する

次に、平方根の計算をするとき、ルート同士の掛け算・割り算が可能になる理由を証明しましょう。そこで、$\sqrt{a}$と$\sqrt{b}$の掛け算をする場面を考えます。

最初に$\sqrt{a}×\sqrt{b}$の2乗をします。「なぜ2乗するのか？」と考えてはいけません。ひとまず2乗します。2乗すると、どうなるでしょうか。掛け算であるため、かっこがあってもなくても意味は同じです。掛け算では、かっこは自由に外すことができます。

例えば、以下の計算は答えが同じです。

• $(2×3)×4=2×3×4$

これを結合法則といいます。そのため、$\sqrt{a}×\sqrt{b}$の2乗は以下のように計算できます。

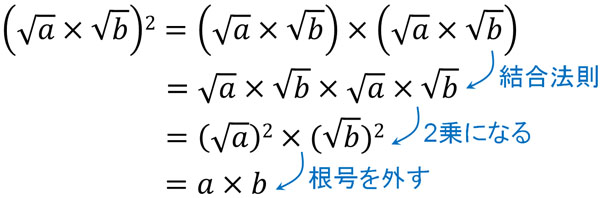
このように、$\left(\sqrt{a}×\sqrt{b}\right)^2=a×b$となります。

次にこの方程式を変換してみましょう。最初、$\sqrt{a}×\sqrt{b}$の2乗をしました。そこで、元の状態に戻すのです。具体的には、両辺に対してルートの記号を付けましょう。

累乗は掛け算の一種です。また、整数は累乗することでルートに変換することができます。つまり、整数をルートにするのは掛け算の一種です。方程式では、両辺に同じものを掛けても問題ありません。この性質を利用して、両辺にルートを付けましょう。そうすると、以下のようになります。

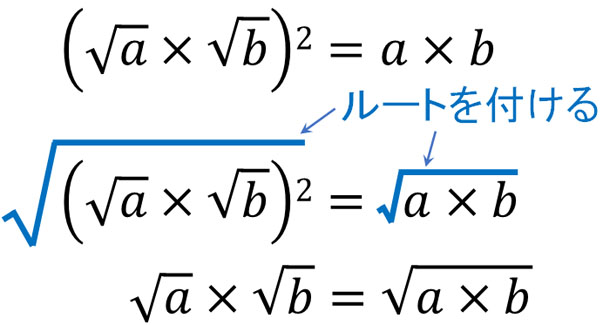
このようにして、$\sqrt{a}×\sqrt{b}=\sqrt{a×b}$と証明することができました。平方根同士掛け算・割り算をできるのは、これまでの数学の知識を使うことで証明できます。

素数を使い、素因数分解を行う

なお平方根の中にある数字はできるだけ小さくする必要があります。その場合、どのようにすればいいのでしょうか。整数を2乗することで、根号にすることができます。同じように、ルートの中に2乗がある場合、整数に変えた後に根号の外へ出すことができます。

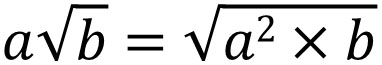
整数をルートにするだけでなく、ルートの一部を整数にすることができます。例えば、以下のようになります。

• $\sqrt{12}=\sqrt{2×2×3}=\sqrt{2^2×3}=2\sqrt{3}$

どのようにすれば、効率的に根号の中に累乗を見つけることができるのでしょうか。その方法が素因数分解です。素数を利用して割り算をするのが素因数分解です。

数字には素数があります。素数とは、「1とその数のみ約数をもつ数」を指します。素数には、例えば以下があります。

• 素数：2、3、5、7、11、13、17、19

例えば、7は1と7しか約数がありません。同じく、11の約数は1と11だけです。それ以外の数で割っても整数になりません。一方で4の約数は1と2と4です。1と4だけでなく、2も約数です。そのため、4は素数ではありません。

整数（自然数）を素数で割ることで、掛け算の式に直すことができます。掛け算の計算の逆が素因数分解だと理解しましょう。

素因数分解というと、言葉が難しいです。そこで、数字を掛け算の式に分解する方法だと理解すれば、素因数分解の概念は簡単です。素数はそれ以上の約分ができません。そこで素数を使えば、掛け算に直すことができます。

どのように素因数分解を行う？掛け算にする手順

それでは、どのようにして素因数分解をすればいいのでしょうか。例として、300を素因数分解してみましょう。

やり方としては、小さい素数から順に割り算をしていきましょう。小さい素数は2です。そこで、2で割り算できるかどうか考えましょう。300を2で割ると、2と150に分けることができます。$300=2×150$です。

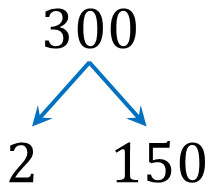
この方法によって、素因数分解を一回することができました。ただ、150は素数ではありません。さらに素数によって割ることができます。そこで、再び素数で割りましょう。2で割ると、以下のようになります。

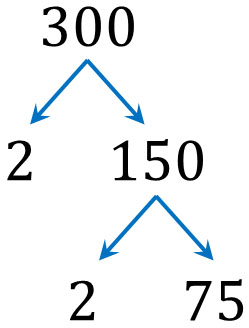
300について、2によって2回割ることで75となります。つまり、$300=2×2×75$です。ただ、75は素数でありません。そこで、さらに素因数分解を進めましょう。

75は2で割れません。そこで、次は3で割ります。

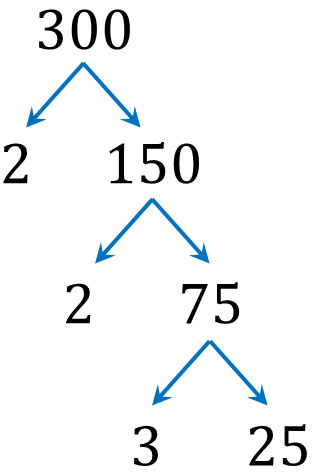
その結果、$300=2×2×3×25$となります。また同じように、素因数分解を進めていきます。25は素数ではなく、5で割ることができます。そのため、以下のようになります。

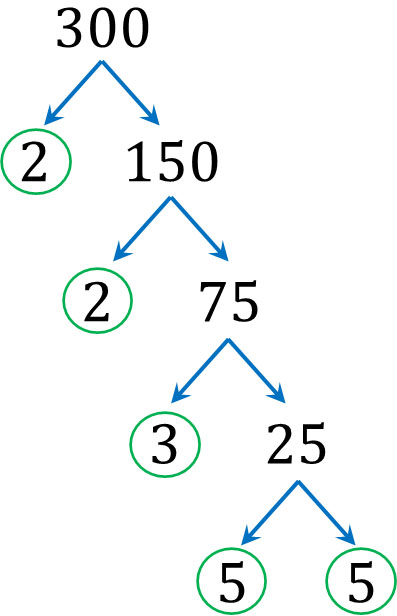
素数で割ることで、最終的に以下の事実が分かりました。

• $300=2×2×3×5×5$

5は素数であるため、それ以上割ることができません。素因数分解では、最後に素数が表れたら割り算をストップします。その後、割った素数と最後に出てきた素数をすべて集めます。上図にある、丸の中にある素数をすべて掛け合わせると300になるため、素因数分解が完了します。

・素因数分解するときの記号

なお実際に素因数分解をするとき、効率的に素早く計算しなければいけません。そのため、上図のような矢印を使って素因数分解をすることはほぼありません。そうではなく、以下のマークを利用します。

使い方としては、記号の中に整数（自然数）を記します。また、記号の左に素数を書きます。以下のようになります。

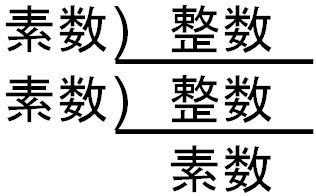
使い方としては、先ほど矢印の図と同じです。素数で割っていくことで、整数を分解していきます。例えば、300の素因数分解では以下のようになります。

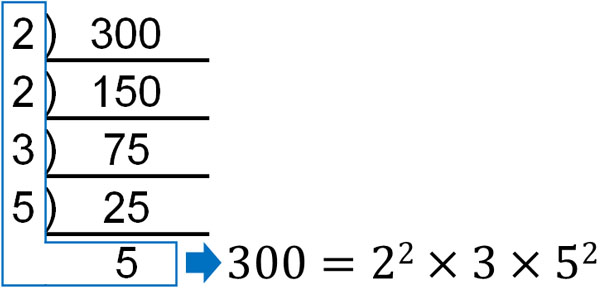
最後に素数が表れた場合、素因数分解は終わりです。その後、素数をすべて集めることで掛け算の式を作れるようになります。矢印の図と意味は同じです。違いとしては、この記号を使うことで、より効率的に素因数分解を行えるようになります。

どの順番で計算しても素因数分解の答えは同じ

ちなみに、素因数分解はどの順番で計算してもいいです。最終的な答えは同じになるからです。例えば、300の素因数分解では以下のように、割り算の順番が違ったとしても同じ答えになります。

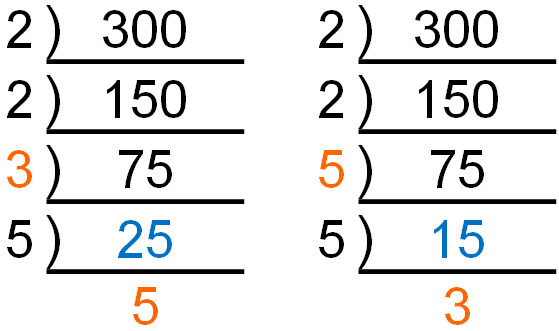
先ほど、「素因数分解では小さい数の素数から順に割り算をしていく」と解説しました。これは、2や3など小さい素数であるほど割り算の計算が簡単になり、ミスが少なくなるからです。ただ場合によっては、大きい素数で割り算をしたほうが計算ミスを防げることがあります。

割り算をしたい整数が偶数の場合、必ず2で割ることができます。一方で奇数の場合、小さい数の素数で割れるかどうか不明なことがあります。

例えば、105はどのような素数で割れるでしょうか。105は3で割ることができます。ただ、3で割れることに気づきにくいです。一方で105を5で割れることについては、簡単に気づくことができます。

「どの順番で素因数分解してもかまわない」という知識は、数学での計算ミスの防止に役立ちます。素因数分解を使うことで、整数を掛け算の式に戻す場合、素数で割るときの順番は気にしないようにしましょう。

根号（ルート）の中にある2乗の数字を外に出す

なぜ、素因数分解を学ぶ必要があるのでしょうか。それは、根号（ルート）の計算で素因数分解を多用するからです。

平方根の計算では、「ルートの中の数字をできるだけ小さくする」というルールがあります。そのためには、素因数分解をしなければいけません。具体的には、根号の中にある2乗の数字を外に出します。

前述の通り、ルートの中に2乗がある場合、根号の外に数字を出すことができます。

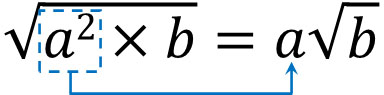
この公式を利用することで、素因数分解をした後にルート内の数字を外に出すことができます。例えば、300を素因数分解することで以下のようになると既に計算しています。

• $300=2×2×3×5×5=2^2×3×5^2$

それでは、$\sqrt{300}$はどのようなやり方で計算すればいいのでしょうか。$\sqrt{300}$は以下のように考えて、ルートの外に数字を出します。

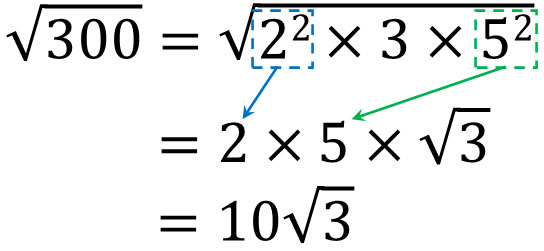
素因数分解を学ぶ理由としては、平方根の計算で利用されるからです。ルート内の数字を外に出すとき、全員が素因数分解をします。

それでは、なぜ根号の中の数字を外に出す必要があるのでしょうか。理由は単純であり、そのほうが数字を理解しやすいからです。例えば、$\sqrt{300}$の数字を瞬時に答えるのは難しいです。一方で$10\sqrt{3}$であれば簡単です。

$\sqrt{3}≒1.73$です。これの10倍であるため、$10\sqrt{3}$は約17.3の値だと分かります。数字がどういう意味をもつのか、理解するための学問が数学です。数字を分かりやすくしなければいけないため、ルート内の数字を外に出さなければいけません。

素数以外の割り算をしてはいけない

なお素因数分解では、素数以外で割り算をしてはいけません。素数以外の数字が混じると、ルート内の数字を外に出せなくなるからです。例えば、300の素因数分解をするとき、4で割るとどうなるでしょうか。

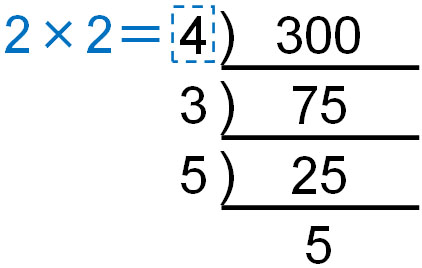
4は2で割ることができるため、素数ではありません。ただ、4で割ってしまうと以下のような式にしてしまう人が多いです。

• $\sqrt{300}=\sqrt{3×4×5^2}$

その結果、答えを$5\sqrt{12}$としてしまいます。この答えは間違いです。ルート内の数字をさらに小さくできるからです。

素数でない数字の場合、4のように、他の数字で割ることができます。その結果、「最も小さい数字を使った掛け算の式」に直すことができません。こうしてルート内の数字が大きくなってしまい、計算ミスを起こします。素因数分解では、必ず素数で割り算をするようにしましょう。

ルート同士の掛け算・割り算の方法を学ぶ

なおルート同士の掛け算・割り算をすることが頻繁にあります。その場合についても、素因数分解をすることで、ルートの外に数字を出しやすくなります。

例えば、以下はどのように計算すればいいでしょうか。

• $\sqrt{15}×\sqrt{21}$

15を素因数分解すると$3×5$です。また、21を素因数分解すると$3×7$です。そのため、以下のように計算できます。

$\sqrt{15}×\sqrt{21}$

$=\sqrt{3×5}×\sqrt{3×7}$

$=\color{red}{\sqrt{3}}×\sqrt{5}×\color{red}{\sqrt{3}}×\sqrt{7}$

$=3×\sqrt{5×7}$

$=3\sqrt{35}$

掛け算をするとき、$\sqrt{15}$と$\sqrt{21}$には素因数分解することによって、それぞれルート内に$\sqrt{3}$が含まれていると分かります。3²の形にすることができるため、3をルートの外に出すことができます。素因数分解することで、どの数字を根号の外に出せるのか理解できます。

なお、累乗を作れない場合はルートの外に数字を出すことができません。先ほどの計算では、ルートの中は$\sqrt{5×7}=\sqrt{35}$と計算しています。3は2乗が存在するものの、5と7は2乗を作れないからです。

ルートの素因数分解を最初に行う

ちなみにルートの掛け算・割り算では、ルート内の数字を小さくすることを最初に行いましょう。掛け算でも割り算でも、数字が小さいほど計算ミスが少なくなります。そのため、平方根の計算では素因数分解を最初に行うといいです。

例えば、以下の問題はどのようにすれば計算ミスが少なくなるでしょうか。

• $\sqrt{28}×\sqrt{18}$

計算方法としては、以下の2通りがあります。

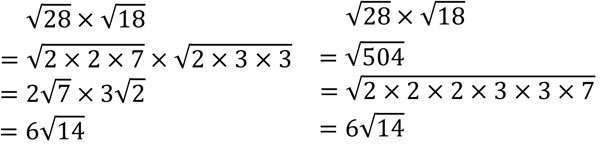
2つの計算方法を確認すると、最初に素因数分解をしたほうが計算が簡単になるのは明らかです。28と18の掛け算は複雑です。また、504の素因数分解をするのは大変です。

この理由から、掛け算でも割り算でも必ず最初に素因数分解をするようにしましょう。そうすれば、計算ミスが少なくなります。

練習問題：平方根の掛け算と割り算

Q1. 次の計算をしましょう

1. $2\sqrt{3}×4\sqrt{21}$
2. $\sqrt{15}×\sqrt{30}$
3. $\sqrt{75}÷2\sqrt{3}$
4. $(3+\sqrt{5})(3-\sqrt{5})$

A1. 解答

(a)

$2\sqrt{3}×4\sqrt{21}$

$=2\sqrt{\color{red}{3}}×4\sqrt{\color{red}{3}×7}$

$=2×4×3×\sqrt{7}$

$=24\sqrt{7}$

(b)

$\sqrt{15}×\sqrt{30}$

$=\sqrt{\color{red}{3}×\color{blue}{5}}×\sqrt{2×\color{red}{3}×\color{blue}{5}}$

$=3×5×\sqrt{2}$

$=15\sqrt{2}$

(c)

割り算がある場合、必ず分数の掛け算に直すようにしましょう。

$\sqrt{75}÷2\sqrt{3}$

$=\sqrt{3×5×5}×\displaystyle\frac{1}{2\sqrt{3}}$

$=5\color{red}{\sqrt{3}}×\displaystyle\frac{1}{2\color{red}{\sqrt{3}}}$

$=\displaystyle\frac{5}{2}$

(d)

平方根の計算では、乗法公式を利用することがあります。以下の公式です。

• $(x+a)(x-a)=x^2-a^2$

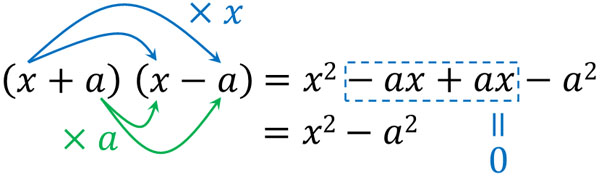
そこで$(x+a)(x-a)=x^2-a^2$の公式を利用することで、ルートの計算をしましょう。

$(3+\sqrt{5})(3-\sqrt{5})$

$=3^2-(\sqrt{5})^2$

$=9-5$

$=4$

根号の掛け算と素数計算を行う

平方根では掛け算と割り算をすることが頻繁にあります。平方根同士は掛け算や割り算をすることができます。通常の掛け算とやり方は同じです。ただ、整数とルートを分けて掛け算または割り算をするルールを理解しましょう。

なお、平方根の計算では必ず素因数分解をしなければいけません。整数を掛け算の式に直すのです。素因数分解をすることで、ルート内の数字を外に出すことができます。

また最初に素因数分解をすることで、平方根の計算が簡単になります。素因数分解を最初にするほうが計算ミスは少なくなるのです。どのようにすれば計算ミスが少なくなるのかについて、そのやり方も含めて理解しましょう。

ルートの掛け算や割り算をするとき、なぜそのような計算になるのかについて、方法だけでなく理由も解説しました。これらを学ぶことで、根号を含む数学の計算が可能になります。