等比数列：公式や等比中項、等比数列の和、対数の計算

数列で学ぶ基本的な内容に等比数列があります。等差数列を学んだあと、等比数列を利用できるようになる必要があります。

特定の値をかけることによって得られる数列が等比数列です。等比数列は金利計算で利用されるなど、私たちの生活でひんぱんに利用される分野でもあります。

そこで等比数列の一般項を得るだけでなく、等比中項や等比数列の和に関する公式を利用できるようになりましょう。また、等差数列と等比数列を組み合わせたり、等比数列と対数を利用する問題を解いたりできるようになりましょう。

それでは、どのように等比数列の公式を利用すればいいのでしょうか。等比数列を用いて計算する方法を解説していきます。

等比数列の一般項を出す公式

特定の値をかけることによって得られる数列を等比数列といいます。例えば初項が2、公比が3の場合、等比数列は以下のようになります。

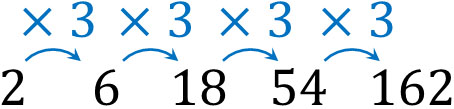
それでは、等比数列の一般項はどうなるのでしょうか。先ほどの例であれば、以下のように考えます。

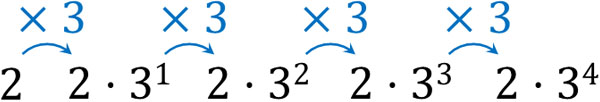
そのため初項\(a\)、公比\(r\)、項数\(n\)の等比数列の一般項\(a_n\)は以下のように表すことができます。

• \(a_n=ar^{n-1}\)

初項と公比がわかれば、公比数列の一般項を得ることができます。

等比中項：等比数列の真ん中の一般項

等比数列を表すとき、通常は初項を基準にします。初項\(a\)、公比\(r\)の場合、数列は以下のようになります。

• \(a,ar,ar^2,ar^3…\)

一方、3つの等比数列について、真ん中の数を\(a\)、公比を\(r\)とすると、以下のように表すこともできます。

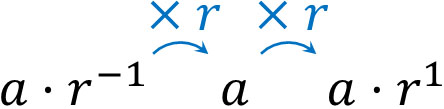
このとき、真ん中の数\(a\)を等比中項といいます。なお上図より、等比数列が\(a,b,c\)の順で並んでいる場合、以下の関係が成り立つとわかります。

• \(b^2=ac\)

これが等比中項で重要な性質です。真ん中の数がわからなくても、両隣の数がわかっている場合、等比中項を得ることができます。それでは、以下の問題の答えは何でしょうか。

• \(a,b,c\)はこの順番で等比数列です。\(a,b,c\)の和が14、積が64のとき、\(a,b,c\)の値を求めましょう。

問題の条件より、以下が成り立ちます。

• \(a+b+c=14\)
• \(abc=64\)

また、等比中項の性質を利用すると以下の式を作れます。

• \(b^2=ac\)

そこで\(b^2=ac\)を\(abc=64\)に代入すると、\(b^3=64\)になります。そのため、\(b=4\)とわかります。そこで\(b=4\)を代入すると、以下の式を作れます。

• \(a=10-c\)
• \(ac=16\)

そこで、\(a=10-c\)を\(ac=16\)に代入しましょう。

\(ac=16\)

\((10-c)c=16\)

\(-c^2+10c=16\)

\(c^2-10c+16=0\)

\((c-2)(c-8)=0\)

\(c=2,8\)

\(c=2\)のとき、\(a=8\)です。また\(c=8\)のとき、\(a=2\)です。そのため、\(2,4,8\)と\(8,4,2\)が答えであるとわかります。

等比数列の和の公式を導出する

それでは、等比数列の和の公式を覚えましょう。等差数列の和の公式と同様に、等比数列の和の公式は覚えなければいけません。

等比数列では2パターンに分けて考える必要があります。初項\(a\)、公比\(r\)、項数\(n\)である等比数列の和について、以下のように考えましょう。

・\(r=1\)の場合

公比が1の場合、初項\(a\)が\(n\)個並ぶことになります。そのため、公比数列の和\(S_n\)は以下のようになります。

• \(S_n=an\)

初項と項数をかけることにより、和を得ることができます。

・\(r≠1\)の場合

多くの場合、公比は1ではありません。そこで\(r≠1\)のときについて、等比数列の和を計算できるようになりましょう。等比数列の和の公式を得るとき、2つの等比数列を利用します。等比数列に対して\(r\)をかけ、以下のように引きましょう。

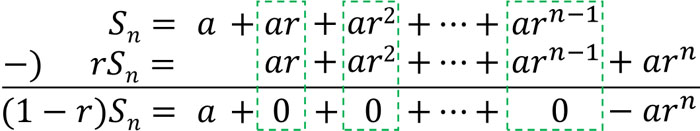
そこで、以下のように計算できます。

\((1-r)S_n=a-ar^n\)

\((1-r)S_n=a(1-r^n)\)

\(S_n=\displaystyle\frac{a(1-r^n)}{1-r}\)

こうして、等比数列の和の公式を得ることができました。なお、分子と分母に\(-1\)をかけることもできます。そのため、以下が等比数列の和の公式です。

• \(S_n=\displaystyle\frac{a(1-r^n)}{1-r}\)\(=\displaystyle\frac{a(r^n-1)}{r-1}\)

それでは、等比数列の和の公式を利用して練習問題を解いてみましょう。以下の問題の答えは何でしょうか。

• 第3項が\(12\)，第4項が\(-24\)である等比数列について、第5項から第8項までの和を求めましょう。

まず、等比数列の一般項を求めましょう。\(a_n=ar^{n-1}\)を利用すると、以下の式を作れます。

• \(a_3=ar^2=12\)
• \(a_4=ar^3=-24\)

そこで\(ar^2=12\)を\(ar^3=-24\)に代入しましょう。

\(ar^3=-24\)

\(12r=-24\)

\(r=-2\)

\(r=-2\)であるため、\(a=3\)です。そのため、一般項は\(a_n=3·(-2)^{n-1}\)です。それでは、どのようにして等差数列の和を計算すればいいのでしょうか。第8項までの和から、第4項までの和を引けば、第5項から第8項の和を得られます。そこで、それぞれを計算しましょう。

・第4項までの和

\(S_4=\displaystyle\frac{3\{1-(-2)^4\}}{1-(-2)}\)

\(S_4=1-16\)

\(S_4=-15\)

・第8項までの和

\(S_8=\displaystyle\frac{3\{1-(-2)^8\}}{1-(-2)}\)

\(S_8=1-256\)

\(S_8=-255\)

そこで、以下のように計算しましょう。

\(S_8-S_4=-255-(-15)=-240\)

こうして、答えは\(-240\)とわかりました。

等差数列と等比数列を利用する計算問題

等比数列の基本を学んだら、応用問題を解けるようになりましょう。等差数列と等比数列の両方が関わる問題は応用問題で出題されることがあります。そこで、以下の問題を解きましょう。

• 数列\(\{a_n\}\)は公比が負である初項1の等比数列です。また、数例\(\{b_n\}\)は\(b_1＝a_3\)、\(b_2＝a_4\)、\(b_3＝a_2\)を満たす等差数列です。数列\(\{a_n\}\)と数列\(\{b_n\}\)を求めましょう。

\(\{a_n\}\)は初項1の等比数列であるため、\(a_n=r^{n-1}\)です。また\(\{b_n\}\)は等差数列であるため、\(b_n=a+(n-1)d\)です。そこで、以下の式を作りましょう。

・\(b_1＝a_3\)より

\(a=r^2\) – ①

・\(b_2＝a_4\)より

\(a+d=r^3\) – ②

・\(b_3＝a_2\)より

\(a+2d=r\) – ③

\(②×2-③\)より、\(a=2r^3-r\)です。また①より、\(a=r^2\)であるため、\(r^2=2r^3-r\)になります。

\(r^2=2r^3-r\)

\(2r^3-r^2-r=0\)

\(r(2r^2-r-1)=0\)

\(r(2r+1)(r-1)=0\)

\(r<0\)であるため、\(r=-\displaystyle\frac{1}{2}\)です。こうして、\(a_n=\left(-\displaystyle\frac{1}{2}\right)^{n-1}\)とわかります。

なお\(a=r^2\)であるため、\(a=\displaystyle\frac{1}{4}\)です。また\(a+2d=r\)であるため、数字を代入して計算しましょう。

\(a+2d=r\)

\(\displaystyle\frac{1}{4}+2d=-\displaystyle\frac{1}{2}\)

\(2d=-\displaystyle\frac{3}{4}\)

\(d=-\displaystyle\frac{3}{8}\)

こうして、\(b_n=\displaystyle\frac{1}{4}-\displaystyle\frac{3}{8}(n-1)\)とわかりました。

等比数列と対数の計算

次の応用問題として、等比数列と対数の計算問題を解きましょう。等比数列は指数計算になるため、項数\(n\)の値が大きくなると、答えも大きくなります（または小さくなります）。そのため、対数を利用するケースがひんぱんにあるのです。

それでは、以下の問題の答えは何でしょうか。

• 初項3、公比2の等比数列\(\{a_n\}\)について、\(10^4<a_n<10^6\)を満たす\(n\)の範囲を求めましょう。なお\(log_{10}2=0.3010\)であり、\(log_{10}3=0.4771\)です。

\(\{a_n\}\)は初項3、公比2の等比数列であるため、\(a_n=3·2^{n-1}\)です。そこで、\(10^4<3·2^{n-1}<10^6\)について対数を加えましょう。

\(log_{10}10^4<log_{10}3·2^{n-1}<log_{10}10^6\)

\(4log_{10}10<log_{10}3+log_{10}2^{n-1}<6log_{10}10\)

\(4<log_{10}3+(n-1)log_{10}2<6\)

\(4<0.4771+0.3010(n-1)<6\)

\(4<0.3010n+0.1761<6\)

\(3.8239<0.3010n<5.8239\)

\(\displaystyle\frac{3.8239}{0.3010}<n<\displaystyle\frac{5.8239}{0.3010}\)

\(12.7…<n<19.3…\)

\(n\)は整数であるため、\(n\)は13から19の範囲となります。こうして、対数を利用することで答えを得ることができました。

等比数列の公式を利用する

等差数列と同様に数列で基本的な内容が等比数列です。等比数列の一般式は必ず覚える必要があり、覚えなければ問題を解くことができません。また、等比中項の性質も学びましょう。

なお、等比数列でひんぱんに利用される公式として等比数列の和があります。数列の問題を解くとき、等比数列の和の公式も必ず覚えなければいけません。

なお数列では応用問題が出されます。等差数列と等比数列を利用する問題が出されたり、等比数列と対数を利用する問題が出題されたりします。ただ、数列が何を意味しているのか理解している場合、問題を解くのは難しくありません。

公式を覚える必要はあるものの、条件通りに値を代入すると問題を解くことが可能です。等比数列は日常生活でもひんぱんに利用される概念であるため、何を意味しているのか理解しましょう。