シグマΣの計算と公式：一般項と等差数列・等比数列の和

数列で学ぶ重要な記号にシグマ（\(Σ\)）があります。計算でひんぱんに利用される記号がシグマであり、公式を必ず覚えなければいけません。

等差数列や等比数列の和を計算するとき、シグマ記号が利用されます。それぞれの数列を計算する場合、多くの時間がかかります。そこで式をまとめたあと、シグマ記号を利用して計算すれば大幅な時間短縮になります。

シグマ記号を利用するためには、一般項を求める必要があります。その後、公式を利用して和を計算しましょう。

それでは、シグマ記号を利用するときの公式や性質には何があるのでしょうか。数列で重要なシグマ記号の計算方法を解説していきます。

1 数列で和を計算するシグマ記号（\(Σ\)）と意味
- 1.1 シグマの計算で必須となる5つの公式
- 1.2 シグマ記号の性質：足し算や引き算、実数倍
2 一般項を求めた後、シグマを利用して計算する
- 2.1 第\(k\)項に\(n\)を含む数列の和
3 シグマを利用して数列の和を計算する

数列で和を計算するシグマ記号（\(Σ\)）と意味

数列で和を計算しなければいけない場面は多いです。ただ、数列では非常に多くの数字を羅列することになります。例えば、数列では以下のように数字が連なります。

\(x_1+x_2+…+x_n\)

そこで、以下のように\(Σ\)を用いて表しましょう。

\(x_1+x_2+…+x_n=\displaystyle\sum_{k=1}^{n}{x_k}\)

シグマを利用すれば、このように簡潔に記すことができます。シグマというのは、\(k\)に1から\(n\)まで代入し、すべて足すことを意味しています。例えば\(\displaystyle\sum_{k=1}^{5}{2k}\)は以下の式を意味します。

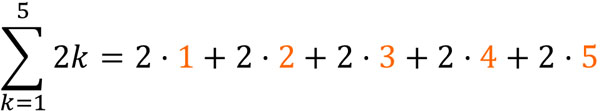
こうした具体例を参考にして、シグマが何を意味しているのか理解しましょう。

シグマの計算で必須となる5つの公式

シグマの計算をするとき、あなたが覚えるべき公式は5つあります。ただ、これらの公式のうち3つはすでに学んでいるため、新たに覚えなければいけない公式は2つ（2乗の和と3乗の和）です。それでは、以下にシグマ記号を利用する公式を記していきます。

・\(a\)が\(n\)個ある数列

\(a\)が\(n\)個並んでいる場合、シグマ記号を利用することで以下のように表すことができます。

\(\displaystyle\sum_{k=1}^{n}{a}=a+a+…+a\)

この場合、\(\displaystyle\sum_{k=1}^{n}{a}=an\)です。説明しなくても、この公式が成り立つ理由を理解できると思います。

・1から\(n\)までの和

数列でひんぱんに利用されるのが、1から\(n\)までの和を意味します。シグマ記号を利用すると以下のように表すことができます。

\(\displaystyle\sum_{k=1}^{n}{k}=1+2+…+n\)

1から\(n\)までの和というのは、初項1、末項\(n\)の等差数列です。そこで等差数列の和の公式に対して、初項1、末項\(n\)を代入しましょう。そうすると、以下の公式を得られます。

\(\displaystyle\sum_{k=1}^{n}{k}=\displaystyle\frac{1}{2}n(n+1)\)

新たな公式として覚えてはいけません。等差数列の和の公式を利用すれば、1から\(n\)までの和を導出できます。

・2乗の和

シグマ記号を学ぶとき、新たに覚えなければいけない内容が2乗の和です。2乗の和はひんぱんに利用されるため、公式を覚えていないと計算問題を解くことができません。二乗の和というのは、以下の足し算を指します。

\(\displaystyle\sum_{k=1}^{n}{k^2}=1^2+2^2+3^2+…+n^2\)

詳細（公式の証明）は省きますが、二乗の和の公式は以下になります。

\(\displaystyle\sum_{k=1}^{n}{k^2}=\displaystyle\frac{1}{6}n(n+1)(2n+1)\)

この公式を覚え、足し算を行えるようになりましょう。

・3乗の和

2乗の和ほど重要ではありませんが、3乗の和を計算することもあります。以下の足し算が3乗の和です。

\(\displaystyle\sum_{k=1}^{n}{k^3}=1^3+2^3+3^3+…+n^3\)

3乗の和の公式は以下になります。

\(\displaystyle\sum_{k=1}^{n}{k^3}=\left\{\displaystyle\frac{1}{2}n(n+1)\right\}^2\)

先ほど、1から\(n\)までの和が\(\displaystyle\sum_{k=1}^{n}{k}=\displaystyle\frac{1}{2}n(n+1)\)になると解説しました。この公式を二乗すると、3乗の和になります。そのため、公式は覚えやすいです。

・等比数列での第\(n\)項までの和

等比数列を学ぶとき、等比数列の和の公式を必ず習います。そのため、等比数列の和の公式はすでに覚えていると思います。初項\(a\)、公比\(r\)、項数\(n\)の等比数列の一般項は\(a_n=ar^{n-1}\)です。

このとき、等比数列の和の公式はシグマ記号と等比数列の一般項を利用して表すことができます。

\(\displaystyle\sum_{k=1}^{n}{ar^{k-1}}=\displaystyle\frac{a(r^n-1)}{r-1}\)

すでに知っている内容であるため、新たに覚えなければいけない公式ではありません。

シグマ記号の性質：足し算や引き算、実数倍

それでは、シグマ記号を使用するときの性質を学びましょう。シグマ記号を含む式について、足し算や引き算、実数倍をするときの方法を理解するのです。

まず、数列の足し算（または引き算）を学びましょう。数列\(\{a_n\}\)の和と数列\(\{b_n\}\)の和には、以下の関係があります。

\(\displaystyle\sum_{k=1}^{n}{(a_k+b_k)}=\displaystyle\sum_{k=1}^{n}{a_k}\)\(+\displaystyle\sum_{k=1}^{n}{b_k}\)

つまり、それぞれの数列の和を計算するとき、先に式の足し算や引き算をした後、シグマを利用して計算できます。

また定数\(p\)について、数列の和の計算では以下の関係が成り立ちます。

\(\displaystyle\sum_{k=1}^{n}{pa_k}=p\displaystyle\sum_{k=1}^{n}{a_k}\)

このように、定数をシグマの外に出すことができます。これらの性質を利用して、シグマを利用する計算問題を解けるようになりましょう。

一般項を求めた後、シグマを利用して計算する

それでは、実際に計算問題を解くことによって数列の和の計算に慣れましょう。数列の和の計算をするとき、まず一般項を得る必要があります。その後、公式を利用して計算しましょう。それでは、以下の数列の和は何でしょうか。

\(1,1+2,1+2+2^2,…\)

一般項を\(a_n\)とすると、一般項は初項1、公比2とする等比数列の和であるとわかります。そのため、一般項は以下のようになります。

\(a_n=\displaystyle\frac{1·(2^n-1)}{2-1}\)

\(a_n=2^n-1\)

そこで、\(a_n\)の和を計算しましょう。以下のようになります。

\(\displaystyle\sum_{k=1}^{n}{(2^k-1)}\)

\(=\displaystyle\sum_{k=1}^{n}{2·2^{k-1}}\)\(-\displaystyle\sum_{k=1}^{n}{1}\)

\(=\displaystyle\frac{2(2^n-1)}{2-1}-n\)

\(=2^{n+1}-n-2\)

こうして、\(a_n\)の和を計算することができました。

第\(k\)項に\(n\)を含む数列の和

なお、応用問題を解けるようになりましょう。具体的には、第\(k\)項に\(n\)を含む場合の数列の和を計算します。言い換えると、初項に\(n\)を含む数列の和を計算しましょう。以下の数列について、和\(S\)はいくらになるでしょうか。

\(S_n=1·n+2·(n-1)+3·(n-2)\)\(+…\)\(+(n-1)·2\)\(+n·1\)

この計算をするため、数列の左側と右側で分けて考えましょう。そうすると、以下のようになります。

・数列の左側

\(1+2+3+…+n-1+n\)

これを一般式にすると、\(a_n=n\)になります。また、第\(k\)項の値は\(k\)です。

・数列の右側

\(n+(n-1)+(n-2)+…+2+1\)

この数列については、初項\(n\)、公差\(-1\)、末項1、項数\(n\)の等差数列とわかります。このとき、第\(k\)項の値は何でしょうか。

注意点として、第\(k\)項の値は\(k+(k-1)·(-1)\)ではありません。項数は\(k\)と連動するものの、初項\(n\)は\(k\)と連動しません。そのため第\(k\)項の式を記すとき、初項\(n\)を\(k\)に変えてはいけません。項数の値が何であっても、初項は\(n\)であるため、第\(k\)項の値は\(n+(k-1)·(-1)\)になります。

例えば第一項の場合、\(k=1\)を代入しましょう。式が\(k+(k-1)·(-1)\)の場合、\(k=1\)だと、値は1になります。第一項（初項）は\(n\)であるため、明らかに間違っています。一方で\(n+(k-1)·(-1)\)に対して\(k=1\)を代入すると、答えは\(n\)になり、初項と一致します。

初項に\(n\)を含む場合、第\(k\)項に\(n\)を含みます。初項に含まれる\(n\)と項数\(n\)は異なる概念であることを認識しましょう。

なお、式をシンプルにするために以下の計算をしましょう。

\(n+(k-1)·(-1)\)

\(n-k+1\)

・第\(k\)項での一般項

それでは、数列の左側の一般項と右側の一般項を利用して、問題文の式での一般項を計算しましょう。第\(k\)項の値は以下のようになります。

\(k(n-k+1)\)

\(=-k^2+kn+k\)

\(=-k^2+k(n+1)\)

この一般項をもつ数列の和は以下のようになります。

\(\displaystyle\sum_{k=1}^{n}{\{-k^2+k(n+1)\}}\)

\(=-\displaystyle\frac{1}{6}n(n+1)(2n+1)\)\(+\displaystyle\frac{1}{2}n(n+1)×(n+1)\)