曲線を取り扱うとき、接線を利用するケースは多いです。二次曲線(放物線、楕円、双曲線)についても、接線を得ることによって計算問題を解けるようになります。
なお二次曲線の接線を学ぶとき、公式を暗記するだけでは不十分であり、公式の証明を行えるようになりましょう。数学の問題では、接線の公式の証明を問われるケースがあるからです。
また公式を利用することにより、計算問題を解けるようになりましょう。ただ二次関数や円を利用して接線の問題を解けるのであれば、二次曲線に関する接線の問題も解けます。計算するときの考え方は同じだからです。
それでは、どのように二次曲線の接線の公式を導出すればいいのでしょうか。また、接線を得る公式を利用してどのように計算問題を解けばいいのでしょうか。放物線や楕円、双曲線で接線を用いる計算方法を解説していきます。
もくじ
放物線、楕円、双曲線の接線の方程式は似ている
二次曲線の接線の方程式を学ぶとき、すべての公式を覚える必要はありません。これらの方程式は似ているからです。
具体的には、放物線の接線の方程式は覚える必要があるものの、楕円と双曲線の方程式は覚えなくてもいいです。楕円と双曲線の接線の方程式は円の接線の方程式とほぼ同じだからです。接点を\((x_1,y_1)\)とすると、それぞれの接線の公式は以下になります。
- 放物線:\(y_1y=2p(x+x_1)\)
- 楕円:\(\displaystyle\frac{x_1x}{a^2}+\displaystyle\frac{y_1y}{b^2}=1\)
- 双曲線:\(\displaystyle\frac{x_1x}{a^2}-\displaystyle\frac{y_1y}{b^2}=1\)、または\(\displaystyle\frac{x_1x}{a^2}-\displaystyle\frac{y_1y}{b^2}=-1\)
ただ、これらの公式を証明できるようにならなければいけません。そこで、どのように証明すればいいのか学びましょう。
放物線の接線の方程式の証明:傾きを利用
まず、放物線の接線の方程式を証明しましょう。接点を\((x_1,y_1)\)、直線の傾きを\(m\)とすると、直線の方程式を\(y=m(x-x_1)+y_1\)と表すことができます。また放物線の方程式は\(y^2=4px\)であるため、この式に代入して整理しましょう。
\(y^2=4px\)
\(\{m(x-x_1)+y_1\}^2=4px\)
\(m^2(x-x_1)^2+2m(x-x_1)y_1\)\(+y_1^2\)\(=4px\)
\(m^2x^2-2m^2x_1x+m^2x_1^2\)\(+2mxy_1-2mx_1y_1\)\(+y_1^2\)\(-4px=0\)
\(m^2x^2-(2m^2x_1-2my_1+4p)x\)\(+m^2x_1^2-2mx_1y_1\)\(+y_1^2\)\(=0\)
一つの接点があるため、放物線と直線は重解をもちます。解の公式で\(\sqrt{b^2-4ac}\)の部分がゼロになるため、解の公式を利用して以下のように\(x\)の解を得ましょう。
- \(x=\displaystyle\frac{2m^2x_1-2my_1+4p}{2m^2}\)
なお接点で重解をもつため、\(x=x_1\)です。そこで先ほどの式に\(x=x_1\)を代入し、傾き\(m\)を計算しましょう。
\(x_1=\displaystyle\frac{2m^2x_1-2my_1+4p}{2m^2}\)
\(2m^2x_1\)\(=2m^2x_1-2my_1+4p\)
\(2my_1=4p\)
\(m=\displaystyle\frac{2p}{y_1}\)
こうして、傾きを得ることができました。そこで直線の方程式\(y=m(x-x_1)+y_1\)に傾きを代入すると、以下の式を得ることができます。
\(y=\displaystyle\frac{2p}{y_1}(x-x_1)+y_1\)
\(y_1y=2p(x-x_1)+y_1^2\)
なお放物線の方程式より、\(y^2=4px\)であるため、接点の座標\((x_1,y_1)\)を利用すると、\(y_1^2=4px_1\)となります。そこで、この式を代入しましょう。
\(y_1y=2p(x-x_1)+y_1^2\)
\(y_1y=2p(x-x_1)+4px_1\)
\(y_1y=2px-2px_1+4px_1\)
\(y_1y=2p(x+x_1)\)
こうして、放物線の接線の方程式を証明できました。
楕円と双曲線の接線の方程式を証明する
次に、楕円の接線の方程式を証明しましょう。楕円の方程式は\(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\)です。また接点を\((x_1,y_1)\)とすると、求める接線の方程式は\(y=m(x-x_1)+y_1\)です。
そこで、以下のように計算しましょう。
\(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\)
\(b^2x^2+a^2y^2=a^2b^2\)
\(b^2x^2+a^2\{m(x-x_1)+y_1\}^2\)\(=a^2b^2\)
\(b^2x^2+a^2m^2(x-x_1)^2\)\(+2a^2my_1(x-x_1)\)\(+a^2y_1^2\)\(=a^2b^2\)
\(b^2x^2\)\(+a^2m^2(x^2-2xx_1+x_1^2)\)\(+2a^2my_1(x-x_1)\)\(+a^2y_1^2\)\(=a^2b^2\)
\((b^2+a^2m^2)x^2\)\(+(-2a^2m^2x_1+2a^2my_1)x\)\(+a^2m^2x_1^2-2a^2mx_1y_1\)\(+a^2y_1^2\)\(-a^2b^2=0\)
この式が重解となればいいため、先ほどと同様に計算すると、\(x\)の解は以下のようになります。
- \(x=\displaystyle\frac{2a^2m^2x_1-2a^2my_1}{2(b^2+a^2m^2)}\)
接点では\(x=x_1\)であるため、この式に\(x=x_1\)を代入して傾きを計算しましょう。
\(x_1=\displaystyle\frac{2a^2m^2x_1-2a^2my_1}{2(b^2+a^2m^2)}\)
\(2x_1(b^2+a^2m^2)=2a^2m^2x_1-2a^2my_1\)
\(2x_1b^2=-2a^2my_1\)
\(m=-\displaystyle\frac{b^2x_1}{a^2y_1}\)
そこで、\(m=-\displaystyle\frac{b^2x_1}{a^2y_1}\)を接線の方程式へ代入しましょう。
\(y=m(x-x_1)+y_1\)
\(y=-\displaystyle\frac{b^2x_1}{a^2y_1}(x-x_1)+y_1\)
\(a^2y_1y=-b^2x_1(x-x_1)\)\(+a^2y_1^2\)
\(a^2y_1y+b^2x_1x\)\(=a^2y_1^2+b^2x_1^2\)
\(\displaystyle\frac{x_1x}{a^2}+\displaystyle\frac{y_1y}{b^2}=\displaystyle\frac{x_1^2}{a^2}+\displaystyle\frac{y_1^2}{b^2}\)
楕円の方程式より、\(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}=1\)であり、接点の座標\((x_1,y_1)\)を代入してもこの方程式は成り立ちます。そのため、以下の式を得られます。
- \(\displaystyle\frac{x_1x}{a^2}+\displaystyle\frac{y_1y}{b^2}=1\)
こうして、楕円の接線の方程式を証明できました。なお双曲線の接線の方程式については、一部の符号が変わるだけであり、同じ計算方法によって証明できます。楕円の接線の方程式を証明できるのであれば、双曲線の接線の方程式を証明できます。
楕円の外側から接線を引く場合の方程式
それでは、接線に関する公式を利用することで計算問題を解けるようになりましょう。以下の問題の答えは何でしょうか。
- 楕円\(\displaystyle\frac{x^2}{16}+\displaystyle\frac{y^2}{12}=1\)に対して、点\((4,6)\)から接線を引くときの式を求めましょう。
接点の座標を\((x_1,y_1)\)とすると、接線の方程式は以下になります。
- \(\displaystyle\frac{x_1x}{16}+\displaystyle\frac{y_1y}{12}=1\)
この直線は\((4,6)\)を通るため、\(x=4\)と\(y=6\)を代入しましょう。
\(\displaystyle\frac{4x_1}{16}+\displaystyle\frac{6y_1}{12}=1\)
\(\displaystyle\frac{x_1}{4}+\displaystyle\frac{y_1}{2}=1\)
\(x_1+2y_1=4\)
\(x_1=4-2y_1\)
また接点は楕円上に存在するため、\(\displaystyle\frac{x_1^2}{16}+\displaystyle\frac{y_1^2}{12}=1\)を満たします。そこで、\(x_1=4-2y_1\)を代入しましょう。
\(\displaystyle\frac{x_1^2}{16}+\displaystyle\frac{y_1^2}{12}=1\)
\(3x_1^2+4y_1^2=48\)
\(3(4-2y_1)^2+4y_1^2=48\)
\(3(16-16y_1+4y_1^2)\)\(+4y_1^2=48\)
\(16y_1^2-48y_1=0\)
\(y_1(y_1-3)=0\)
\(y_1=0,3\)
\(y_1=0\)のとき、\(x_1=4\)であるため、接線は\(x=4\)です。また\(y_1=3\)のとき、\(x_1=-2\)であるため、接線は\(\displaystyle\frac{-2x}{16}+\displaystyle\frac{3y}{12}=1\)です。
\(\displaystyle\frac{-2x}{16}+\displaystyle\frac{3y}{12}=1\)
\(\displaystyle\frac{-x}{8}+\displaystyle\frac{y}{4}=1\)
\(-x+2y=8\)
こうして\(x=4\)に加えて、もう一つの接線\(-x+2y=8\)を得ることができました。
二次曲線の接線と証明問題
次に、接線の方程式を利用することで証明問題を解きましょう。以下の問題の答えは何でしょうか。
- 放物線\(y^2=4px\)(\(p>0\))の上に点Q\((x_1,y_1)\)があります。点Qでの接線と\(x\)軸との交点をA、放物線の焦点をF\((p,0)\)とします。この場合、\(∠QAF=∠AQF\)になると証明しましょう。なお\(x_1>0\)、\(y_1>0\)です。
図を作ると以下のようになります。
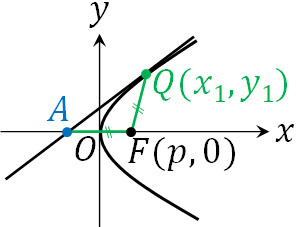
2つの角度が等しい場合、二等辺三角形を作ることができます。そのため\(∠QAF=∠AQF\)の場合、\(AF=QF\)となります。そこで\(AF=QF\)を示すことによって\(∠QAF=∠AQF\)を証明しましょう。
点Aは\(x\)軸上に存在するため、\(y=0\)です。また、点Qでの接線の方程式は\(y_1y=2p(x+x_1)\)です。点Aは接線上に存在するため、接線の方程式に\(y=0\)を代入して計算しましょう。
\(0=2p(x+x_1)\)
\(x=-x_1\)
こうして、点Aの座標は\((-x_1,0)\)とわかります。つまり、AFの長さは\(p+x_1\)です。次に、QFの長さを計算しましょう。
\(QF=\sqrt{(x_1-p)^2+y_1^2}\)
\(QF=\sqrt{(x_1-p)^2+4px_1}\)
\(QF=\sqrt{(x_1+p)^2}\)
\(QF=x_1+p\)
\(AF=QF\)であるため、△AFQは二等辺三角形です。こうして、\(∠QAF=∠AQF\)になると証明できました。
放物線、楕円、双曲線と接線の公式を学ぶ
接線を利用して図形の問題を解かなければいけないケースは多いです。そこで放物線、楕円、双曲線について、接線の公式を利用しましょう。
このとき、接線の公式を導出できるようになりましょう。傾き\(m\)と直線の方程式を利用することにより、接線の公式を証明できます。なお放物線の接線の方程式は覚える必要があるものの、楕円と双曲線の接線の方程式は円の接線の方程式と似ているため、覚える必要はありません。
なお接線を得る公式を利用することにより、計算問題を解けるようになりましょう。計算方法は二次関数や円と同じであるため、これらの問題を解ける場合は難しくありません。
新たな公式を覚える必要はあるものの、接線を得る公式を利用することにより、二次曲線で接線を用いて計算できるようになります。接線を用いることにより、計算問題を解けるようになりましょう。






