二次関数を学ぶとき、\(y=x^2\)のような簡単な式ではなく、より複雑な式を理解しなければいけません。
二次関数ではグラフを描くことができます。ただ二次関数の頂点を見つけるためには、二次関数の式を変形しなければいけません。このときに行う作業が平方完成です。平方完成を利用することによって、グラフの頂点がわかるようになります。
また、二次関数のグラフを移動させることがあります。グラフを移動させることによって、二次関数の頂点がどこにくるのか理解しなければいけません。なお、グラフの移動には平行移動と対称移動の二種類があります。
平方完成や二次関数の移動というのは、二次関数の基本となります。そこでどのように二次関数のグラフを理解すればいいのか解説していきます。
もくじ
関数とは何か
まず、関数とは何かをおさらいしましょう。関数というのは、何か数字を入れたとき、答えが出てくる式を指します。関数は\(y=f(x)\)で表されます。
\(y=f(x)\)という記号を見ると、難しいように思えてしまいます。ただ実際には難しくなく、「\(x\)に何か値を入れたとき、\(y\)の値が決まる」のが関数と理解しましょう。例えば\(y=2x\)という関数はどのように考えればいいでしょうか。
\(f(2)\)というは、\(x\)に2を代入することを意味します。関数が\(y=2x\)の場合、\(y=4\)です。一方で\(f(3)\)の場合、\(y=6\)です。
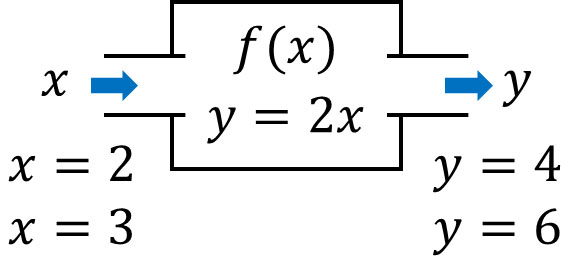
このように、\(x\)の数字を決めると\(y\)の数字が出てくるのが関数です。
二次関数のグラフと式、頂点の場所
それでは、二次関数のグラフはどのように考えればいいのでしょうか。最も簡単な二次関数は以下のような式になります。
- \(y=x^2\)
- \(y=3x^2\)
- \(y=-2x^2\)
これらは\(y=ax^2\)の式で表される式です。これらの二次関数では、頂点は必ず原点になります。\(x=0\)を代入すると、\(y=0\)になるからです。
一方、頂点が原点ではない二次関数はどのような式で表されるのでしょうか。以下の式によって表される二次関数の場合、原点が頂点ではありません。
- \(y=a(x-p)^2+q\)
例えば、以下のような二次関数の式になります。
- \(y=(x-2)^2+3\)
- \(y=2(x-1)^2-2\)
- \(y=-(x+3)^2+3\)
これらの二次関数の頂点はどこでしょうか。それぞれの二次関数について、グラフを描いてみましょう。以下のようになります。
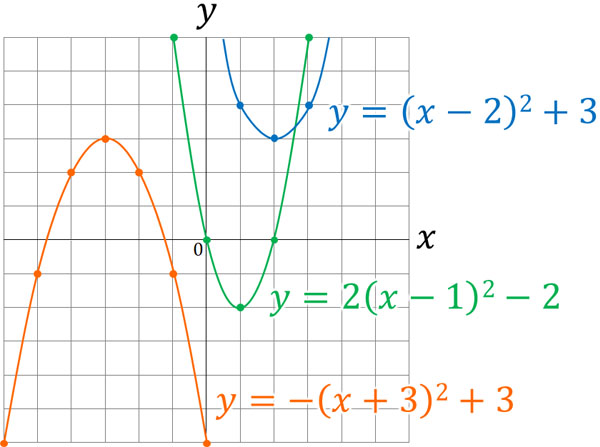
\(y=x^2\)のグラフの頂点は\((0,0)\)です。\(x\)に0を代入することによって、\(x^2=0\)となるからです。
同じように考えましょう。例えば\(y=(x-2)^2+3\)の場合、\(x\)に2を代入すると、\((x-2)^2=0\)となります。また、このときの\(y\)の値は3です。そのため、\(y=(x-2)^2+3\)の頂点は\((2,3)\)です。同じように考えると、\(y=2(x-1)^2-2\)の頂点は\((1,-2)\)です。\(y=-(x+3)^2+3\)の頂点は\((-3,3)\)です。
\(x\)に数字を代入するとき、二乗の式がゼロになる\(x\)の値を見つけましょう。その後、\(y\)座標も決まります。そうすれば頂点の座標がわかります。つまり\(y=a(x-p)^2+q\)という二次関数では、頂点は必ず\((p,q)\)になります。
なお\(y=(x-2)^2+3\)というのは、\(y=x^2\)のグラフを右に2、上に3動かした二次関数です。
ちなみに\(y=(x-2)^2+3\)や\(y=2(x-1)^2-2\)では、下向きに尖った形をしています。このような二次関数のグラフを「下に凸」といいます。一方、\(y=-(x+3)^2+3\)では上向きに尖った形をしています。このような二次関数のグラフを「上に凸」といいます。
二次関数の一般的な式を理解する
一方、二次関数では一般的に表される式があります。例えば一次関数では、\(y=ax+b\)の式で表されます。二次関数にも、同じように一般的な式があります。それが以下になります。
- \(y=ax^2+bx+c\)
例えば、以下のような式が二次関数の一般的な式です。
- \(y=x^2-4x+7\)
- \(y=2x^2-4x\)
- \(y=-x^2-6x-6\)
\(y=ax^2+bx+c\)は二次関数であるため、グラフを描くと必ず放物線となります。
平方完成によって二次関数の式を変える
ただ\(y=ax^2+bx+c\)では、どこが頂点なのかわかりません。そこで、\(y=ax^2+bx+c\)の式を\(y=a(x-p)^2+q\)の形に変えるようにしましょう。これを平方完成といいます。
- \(y-ax^2+bx+c⇔y=a(x-p)^2+q\)
平方完成には公式があります。ただ平方完成の公式は複雑であり、覚えないようにしましょう。そこで公式は利用せず、「どのように平方完成をすればいいのか」について、やり方を学ぶといいです。
以下の手順によって平方完成をします。
- \(a\)を利用して因数分解し、カッコをもつ式を作る
- カッコの中で、二乗の式へ因数分解できる式を作る
- 不要な数をカッコの外に出し、二乗の式を作る
この説明では理解できないと思うので、実際に平方完成をしてみましょう。
・平方完成を行う
例として、\(y=x^2-4x+7\)の平方完成をします。\(y=x^2-4x+7\)と\(y=ax^2+bx+c\)を比べると、\(a=1\)です。そのため、今回は\(a\)を利用して因数分解する必要はありません。そこで、次にカッコをもつ式を作りましょう。
\(y=x^2-4x+7\)
\(y=(x^2-4x)+7\)
その後、カッコの中に因数分解できる式を作る必要があります。因数分解をするとき、二乗の式を作るには以下の公式を利用します。
- \((x+a)^2=x^2+2ax+a^2\)
- \((x-a)^2=x^2-2ax+a^2\)
\(y=(x^2-4x)+7\)をみて、どのようにすれば\(x^2-2ax+a^2\)の式を作ることができるでしょうか。そこで、\(y=(x^2\color{red}{-4x})+7\)の\(-4x\)に着目しましょう。\(-4x\)の係数は-4です。そこで、-4を-2で割りましょう。
なぜ-2で割るかというと、\(x^2-2ax+a^2\)を作る必要があるからです。\(y=(x^2\color{red}{-4x})+7\)と\(y=x^2\color{red}{-2ax}+a^2\)を比較すると、\(-4x=-2ax\)になる必要があるため、\(-4=-2a\)となります。そこで、\(a\)の値をみつけるため、-2で割るのです。そうすると、\(a=-4÷-2=2\)となります。
\((x-2)^2=x^2-4x+4\)です。ただ\(y=(x^2-4x)+7\)と\(x^2-4x+4\)を比較すると、明らかに式が違います。そこで、\(y=(x^2-4x)+7\)を以下のように変えましょう。
\(y=(x^2-4x)+7\)
\(y=(\color{red}{x^2-4x+4}-4)+7\)
\(y=(x^2-4x+4)+3\)
\((x-2)^2=x^2-4x+4\)です。そのため因数分解をすることによって、以下の式に変えることができます。
\(y=(x^2-4x+4)+3\)
\(y=(x-2)^2+3\)
こうして、\(y=x^2-4x+7\)から\(y=(x-2)^2+3\)の式に変えることができます。
・平方完成に慣れる
そこでは、ほかの二次関数についても平方完成をしましょう。以下の式はどのように平方完成すればいいでしょうか。
- \(y=2x^2-4x\)
- \(y=-x^2-6x-6\)
まず、\(y=2x^2-4x\)を平方完成しましょう。\(y=ax^2+bx+c\)を比べると、\(a=2\)です。そこで、2を利用して因数分解しましょう。
\(y=2x^2-4x\)
\(y=2(x^2-2x)\)
次に、\(y=2(x^2-2x)\)の式を利用して、\(x^2-2ax+a^2\)を作りましょう。\(y=2(x^2\color{red}{-2x})\)のうち、\(-2x\)に着目します。係数は-2であるため、-2を-2で割ると答えは1です。そのため、以下の式を作ることができます。
\(y=2(x^2-2x)\)
\(y=2(\color{red}{x^2-2x+1}-1)\)
\(y=2(x^2-2x+1)-2\)
次に因数分解しましょう。
\(y=2(x^2-2x+1)-2\)
\(y=2(x-1)^2-2\)
こうして、平方完成することができます。
一方、\(y=-x^2-6x-6\)の平方完成はどうすればいいでしょうか。まず、-1を利用して因数分解しましょう。
\(y=-x^2-6x-6\)
\(y=-(x^2+6x)-6\)
次に\(6x\)に着目して、二乗の式へ変換できる式を作ります。なお、今回は\(x^2\color{red}{+}2ax+a^2\)の式を作る必要があります。そのため先ほどとは異なり、-2ではなく2で割りましょう。\(6x=2ax\)にする必要があり、\(6=2a\)となるからです。\(a=6÷2=3\)です。そのため、\((x+3)^2\)の式を作るために以下のように式を変えます。
\(y=-(x^2+6x)-6\)
\(y=-(\color{red}{x^2+6x+9}-9)-6\)
\(y=-(x^2+6x+9)+3\)
\(y=-(x+3)^2+3\)
こうして、平方完成することができます。
平行移動による二次関数のグラフの移動
次に、二次関数のグラフを平行移動するとき、グラフの頂点がどこに来るのか理解しましょう。グラフを平行移動させるため、グラフの形は変わりません。しかし、頂点の場所が異なります。
先ほど\(y=(x-2)^2+3\)というのは、\(y=x^2\)のグラフを右に2つ、上に3つ移動させたグラフであると説明しました。\(y=(x-2)^2+3\)の頂点は\((2,3)\)だからです。
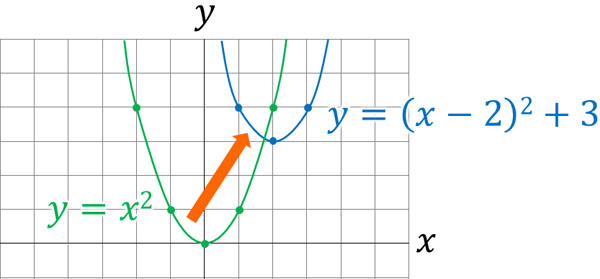
つまり二次関数のグラフを平行移動させるためには、\(y=(x-p)^2+q\)の式を確認して、頂点を動かせばいいとわかります。例えば\(y=x^2\)の式を左に4つ、下に2つ動かす場合、式は以下のようになります。
- \(y=(x+4)^2-2\)
\(y=(x+4)^2-2\)では、頂点は\((-4,-2)\)です。このように\(y=(x-p)^2+q\)を確認して、\(p\)と\(q\)の値を変えることによって頂点を移動させましょう。そうすれば、二次関数のグラフを平行移動させることができます。
・\(y=ax^2+bx+c\)の式を平行移動させる
それでは一般式である\(y=ax^2+bx+c\)を与えられるとき、二次関数を平行移動させるにはどのようにすればいいのでしょうか。\(y=ax^2+bx+c\)では頂点がわからないため、平方完成しましょう。例えば、以下の式のグラフを左に3つ、下に4つ動かす場合、どのような二次関数になるでしょうか。
- \(y=x^2-4x+7\)
先ほど説明した通り、\(y=x^2-4x+7\)を平方完成すると以下の関数に変えることができます。
- \(y=(x-2)^2+3\)
このように平方完成すれば頂点がわかります。頂点がわかれば、平行移動させた後の関数がわかります。\(y=(x-2)^2+3\)を左に3つ、下に4つ動かすため、以下の関数を作れます。
- \(y=(x+1)^2-1\)
\(y=(x+1)^2-1\)の頂点は\((-1,-1)\)です。また、\(y=(x-2)^2+3\)の頂点は\((2,3)\)です。\((2,3)\)から左に3つ、下に4つ動かせば、頂点は\((-1,-1)\)と重なります。そのため、平行移動によって\(y=(x+1)^2-1\)になるのです。このようにして答えを出します。
対称移動による二次関数のグラフの移動
なお、二次関数の移動では平行移動のほかにも対称移動があります。対称移動では\(x\)軸や\(y\)軸、原点を利用して二次関数を移動させます。
\(x\)軸対称、\(y\)軸対称、原点対称のグラフがどのようになるのか以下で確認しましょう。
- \(x\)軸対称:頂点が\((x,y)\)から\((x,-y)\)になる
- \(y\)軸対称:頂点が\((x,y)\)から\((-x,y)\)になる
- 原点対称:頂点が\((x,y)\)から\((-x,-y)\)になる
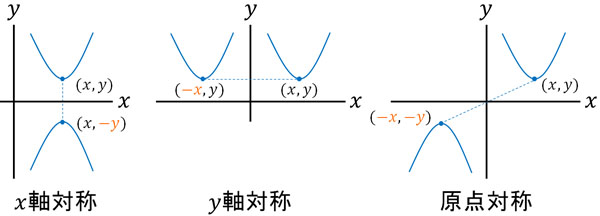
このように二次関数の形は変わらないものの、頂点の位置が移動します。そのため、\(y=f(x)\)の関数について、対称移動では以下のようになります。
- \(x\)軸対称:\(-y=f(x)\)
- \(y\)軸対称:\(y=f(-x)\)
- 原点対称:\(-y=f(- x)\)
それでは、対称移動によって二次関数がどのように変わるのか確認しましょう。
・\(x\)軸対称
例えば\(y=x^2-4x+7\)の\(x\)軸対称はどのようなグラフでしょうか。\(-y=f(x)\)にする必要があるため、\(x\)軸対称では以下の関数になります。
\(-y=x^2-4x+7\)
\(y=-x^2+4x-7\)
・\(y\)軸対称
\(y=x^2-4x+7\)の\(y\)軸対称どのようになるでしょうか。\(y\)軸対称では\(y=f(-x)\)となるため、\(x\)に\(-x\)を代入しましょう。
\(y=(-x)^2-4(-x)+7\)
\(y=x^2+4x+7\)
・原点対称
\(y=x^2-4x+7\)の原点対称はどのようになるでしょうか。原点対称の場合、\(x\)と\(y\)の両方の符号が変わります。原点対称では\(-y=f(-x)\)となるため、以下のようになります。
\(-y=(-x)^2-4(-x)+7\)
\(-y=x^2+4x+7\)
\(y=-x^2-4x-7\)
このようにして二次関数を対称移動させます。
頂点を利用し、二次関数を決定する
なお頂点がわかれば、二次関数を決定することができます。\(y=a(x-p)^2+q\)または\(y=ax^2+bx+c\)を利用することによって二次関数を得るのです。
なお頂点や軸が与えられている場合、\(y=a(x-p)^2+q\)を利用します。一方で頂点や軸が与えられていない場合、\(y=ax^2+bx+c\)を利用して二次関数を出すようにしましょう。
・頂点や軸がわかっている場合
例えば頂点が\((2,1)\)であり、点\((1,2)\)を通る二次関数は何でしょうか。頂点がわかっているため、\(y=a(x-p)^2+q\)に代入しましょう。以下のようになります。
- \(y=a(x-2)^2+1\)
また、この二次関数は点\((1,2)\)を通ります。そこで、\(x=1,y=2\)を代入しましょう。以下のようになります。
\(2=a(1-2)^2+1\)
\(2=a+1\)
\(a=1\)
こうして、二次関数は\(y=(x-2)^2+1\)であるとわかります。
・頂点や軸がわからない場合
一方、頂点を与えられていないこともあります。その場合、\(y=ax^2+bx+c\)を利用しましょう。例えば点\((1,2)\)、点\((2,1)\)、点\((4,5)\)を通る二次関数はなんでしょうか。
答えを出すため、それぞれの座標を代入しましょう。以下のようになります。
- 点\((1,2)\):\(2=a+b+c\) -①
- 点\((2,1)\):\(1=4a+2b+c\) -②
- 点\((4,5)\):\(5=16a+4b+c\) -③
そこで連立方程式を利用し、それぞれの値を出すようにしましょう。
- \(③-②\):\(4=12a+2b\)
- \(①-②\):\(1=-3a-b\)
次に、以下の連立方程式を解きます。
\(\begin{eqnarray} \left\{\begin{array}{l}4=12a+2b\\1=-3a-b\end{array}\right.\end{eqnarray}\)
この連立方程式を解くと、\(a=1,b=-4\)とわかります。次に①に代入すると、\(c=5\)とわかります。そのため、二次関数は\(y=x^2-4x+5\)です。
二次関数の平方完成と移動を理解する
\(y=ax^2+bx+c\)で表されるのが二次関数です。ただ\(y=ax^2+bx+c\)では、どこが頂点になるのかわかりません。そこで平方完成をすることによって頂点を調べましょう。
平方完成をするためには因数分解をしなければいけません。そこで\((x+a)^2\)または\((x-a)^2\)の式を作りましょう。これによって平方完成をすることができ、二次関数の頂点がわかります。
また頂点がわかれば、二次関数を平行移動させることができます。平方完成させた後、頂点の場所を変えることによって関数を移動できます。グラフの形は同じであるものの、平行移動では頂点のみ移動することになります。また、同時に対称移動の方法も理解しましょう。
ここまでの内容は二次関数の基本です。そこで、どのように平方完成や二次関数の移動をすればいいのか理解しましょう。






