特定の条件を満たす点について、点が動くことによって完成される軌道の方程式を計算できるようになりましょう。
点というのは、特定の座標にとどまっているとは限らず、動いていることがひんぱんにあります。このとき点が描く軌道としては、直線や放物線、円などさまざまです。軌道の方程式を計算するには手順があるため、具体的な方法を覚えましょう。
また軌道の方程式を得られるようになるためには、さまざまな練習問題を解く必要があります。このとき、除外点が存在することに注意しなければいけません。
それでは、どのように軌道の方程式を計算すればいいのでしょうか。数学で重要な軌道の方程式の計算方法を解説していきます。
もくじ
軌道の方程式を求める手順
方程式を利用することにより、特定の図形を表すことができます。点が動くとき、点の軌道を方程式によって表せるようになりましょう。
軌道の方程式を求めるとき、正しい手順があります。軌道の計算問題を解くとき、求めたい軌道の座標を\((x,y)\)と表すようにしましょう。
求めたい座標以外の点についても、文字を利用して表したいケースは多いです。この場合、\(x,y\)以外の文字を利用して点を表しましょう。例えば、\((a,b)\)や\((s,t)\)と座標を設定するのです。
その後、\(a,b\)や\(s,t\)などの文字を消すと、軌道の方程式を得られるようになります。それでは、実際に練習問題を解くことで軌道の方程式を計算できるようになりましょう。
軌道による円の方程式:アポロニウスの円
2つの点について、距離の割合が一定になるように新たな点を設定するとき、得られる軌道をアポロニウスの円といいます。それでは、以下の問題の答えは何でしょうか。
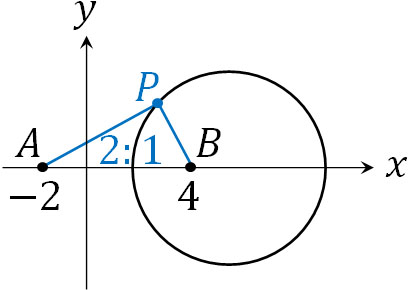
- 2点A\((-2,0)\)とB\((4,0)\)からの距離の比が2:1となる点Pの軌道を求めましょう。
点Pの軌道を\((x,y)\)としましょう。点Aと点Bについて、点Pからの距離の比が2:1になるため、以下の関係となります。
\(AP:BP=2:1\)
そのため、以下のようになります。
\(AP=2BP\)
\(AP^2=4BP^2\)
そこで、三平方の定理を利用することで以下のように計算しましょう。
\((x+2)^2+y^2=4(x-4)^2+4y^2\)
\(x^2+4x+4=4(x^2-8x+16)+3y^2\)
\(3x^2+3y^2-36x+60=0\)
\(x^2+y^2-12x+20=0\)
こうして、点Pによる軌道の方程式を得ることができました。
重心の軌道と除外点
なお軌道の方程式を計算するとき、除外点の存在を認識しましょう。場合によっては、除外しなければいけない点が存在するのです。
それでは、どのようなときに除外点を考慮すればいいのでしょうか。実際に問題を解いて確認しましょう。
- 点A\((3,0)\)と点B\((0,3)\)に加え、円\(x^2+y^2=9\)上を動く点Pの3つを頂点とする三角形の重心Gの軌道を求めましょう。
点Pは動くため、重心Gも動きます。求めたい軌道は点Gです。そこで点Gの座標を\((x,y)\)、点Pの座標を\((a,b)\)としましょう。
点Pは円\(x^2+y^2=9\)の上を動くため、\(a^2+b^2=9\)です。また点Gは重心であるため、\(x\)座標と\(y\)座標は以下のようになります。
- \(x\)座標:\(\displaystyle\frac{3+0+a}{3}\)
- \(y\)座標:\(\displaystyle\frac{0+3+b}{3}\)
\(x=\displaystyle\frac{3+a}{3}\)であるため、\(a=3x-3\)です。また\(y=\displaystyle\frac{3+b}{3}\)であるため、\(b=3y-3\)です。そこで、\(a^2+b^2=9\)に代入しましょう。
\(a^2+b^2=9\)
\((3x-3)^2+(3y-3)^2=9\)
\((x-1)^2+(y-1)^2=1\)
こうして、多くの人は\((x-1)^2+(y-1)^2=1\)が正解と考えます。ただ、この状態では不完全です。なぜ、\((x-1)^2+(y-1)^2=1\)が答えではないのでしょうか。それは、除外点を考慮していないからです。以下のように図を作って考えてみましょう。
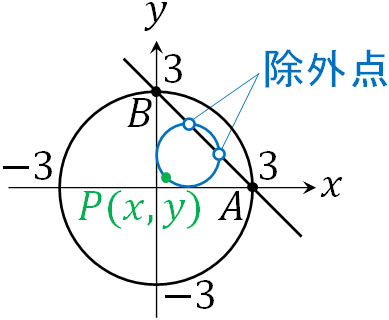
AB上の点では、三角形を作ることができません。つまり、重心は存在しません。そこで、直線ABと円\((x-1)^2+(y-1)^2=1\)の交点は除外しなければいけません。
図より、直線ABの方程式は\(y=-x+3\)です。そこで、直線ABと円\((x-1)^2+(y-1)^2=1\)の交点を求めましょう。
\((x-1)^2+(y-1)^2=1\)
\((x-1)^2+(-x+2)^2=1\)
\(2x^2-6x+4=0\)
\(x^2-3x+2=0\)
\((x-2)(x-1)=0\)
\(x=1,2\)のとき、円と直線は交わります。そこで\(y\)座標も計算すると、\((1,2)\)と\((2,1)\)となります。つまり\((1,2)\)と\((2,1)\)の座標では、三角形を作れないとわかります。そのため、答えは以下のようになります。
- 円\((x-1)^2+(y-1)^2=1\)、ただし点\((1,2)\)と点\((2,1)\)を除く。
軌道の問題を解く場合、図を描くことにより、条件を満たさない点が存在するかどうかを確かめる必要があります。軌道の方程式を得るとき、除外点が存在することに気を付けなければいけません。
角の二等分線・線対称な直線の方程式
先ほど、円軌道の方程式を計算しました。それでは、軌道が直線を描く場合はどのように方程式を計算すればいいのでしょうか。先ほどと同じように、条件を利用して方程式を得ましょう。
例題として、以下の問題を解きましょう。
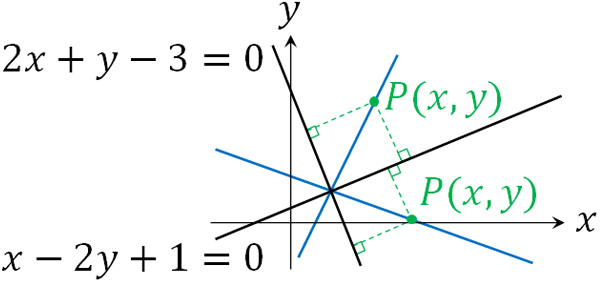
- 2つの直線\(2x+y-3=0\)と\(x-2y+1=0\)のなす角の二等分線の方程式を求めましょう。
まず、求める軌道を点P\((x,y)\)としましょう。角の二等分線では、点と2つの直線は必ず等距離になります。そこで点と直線の距離を求める公式を利用して軌道の計算をしましょう。以下のようになります。
\(\displaystyle\frac{|2x+y-3|}{\sqrt{2^2+1^2}}=\displaystyle\frac{|x-2y+1|}{\sqrt{1^2+(-2)^2}}\)
\(\displaystyle\frac{|2x+y-3|}{\sqrt{5}}=\displaystyle\frac{|x-2y+1|}{\sqrt{5}}\)
\(|2x+y-3|=|x-2y+1|\)
\(2x+y-3=±(x-2y+1)\)
こうして、軌道の方程式は\(x+3y-4=0\)と\(3x-y-2=0\)になるとわかります。
他の軌道を計算するときについても、同様に条件を利用して軌道の方程式を得ましょう。以下の問題の答えは何でしょうか。
- 直線\(y=2x\)を基準にして、直線\(3x+y=15\)に対して対称な直線の方程式を求めましょう。
求める直線上の座標を点P\((x,y)\)とします。また、直線\(3x+y=15\)上の点Qを\((a,b)\)とすると、\(3a+b=15\)が成り立ちます。つまり、\(b=-3a+15\)です。
このとき、点Pと点Qの中点はそれぞれ以下のようになります。
- \(x\)座標:\(\displaystyle\frac{x+a}{2}\)
- \(y\)座標:\(\displaystyle\frac{y+b}{2}\)
\(y=2x\)を基準にして点Pと点Qは線対称であるため、点Pと点Qの中点は直線\(y=2x\)上にあります。そこで、以下の式を作りましょう。
\(\displaystyle\frac{y+b}{2}=2×\displaystyle\frac{x+a}{2}\)
\(y+b=2x+2a\)
\(b=-3a+15\)であるため、以下のように計算しましょう。
\(y+(-3a+15)=2x+2a\)
\(2x-y=-5a+15\) – ①
また線対称の性質より、直線PQは\(y=2x\)に対して垂直であるため、以下の式を作れます。
\(2×\displaystyle\frac{y-b}{x-a}=-1\)
\(2y-2b=a-x\)
\(2y-2(-3a+15)=a-x\)
\(x+2y=-5a+30\) – ②
\(①-②\)より、
\(x-3y=-15\)
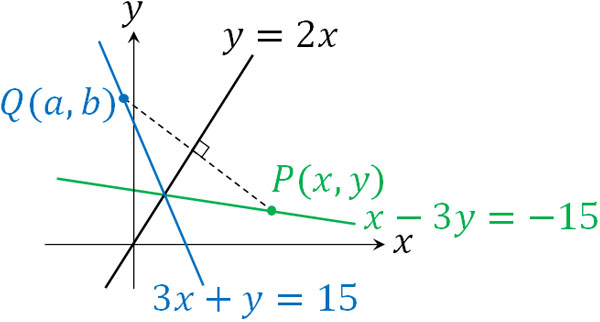
こうして、答えは\(x-3y=-15\)とわかりました。求める座標を\((x,y)\)と設定するとき、\((a,b)\)や\((s,t)\)など、その他の座標に関する文字を消すようにしましょう。
2直線の交点の軌道と除外点
次に、2つの直線によって作られる交点の軌道を計算しましょう。以下の問題の答えは何でしょうか。
- 2つの直線\(y=ax-a-2\)と\(y=bx+3b\)は互いに垂直を保ち、平面上を動いています。\(a,b\)が実数であるとき、2つの直線による交点Pの軌道を求めましょう。
2つの直線は垂直であるため、\(ab=-1\)です。また点Pの座標を\((x,y)\)とすると、点Pは\(y=ax-a-2\)と\(y=bx+3b\)の両方の条件を満たします。このとき\(ab=-1\)より、\(b=-\displaystyle\frac{1}{a}\)であるため、以下のように計算できます。
\(y=bx+3b\)
\(y=-\displaystyle\frac{x}{a}-\displaystyle\frac{3}{a}\)
\(ay=-x-3\)
\(a=\displaystyle\frac{-x-3}{y}\)
そこで、\(a=\displaystyle\frac{-x-3}{y}\)を\(y=ax-a-2\)に代入しましょう。
\(y=ax-a-2\)
\(y=a(x-1)-2\)
\(y=\displaystyle\frac{-x-3}{y}(x-1)-2\)
\(y^2=-(x+3)(x-1)-2y\)
\(y^2=-(x^2+2x-3)-2y\)
\(x^2+y^2+2x+2y-3=0\)
ただ、答えが\(x^2+y^2+2x+2y-3=0\)では不十分です。除外点を考慮していないからです。そこで、図を作りましょう。\(x^2+y^2+2x+2y-3=0\)を変形すると以下のようになります。
\(x^2+y^2+2x+2y-3=0\)
\((x+1)^2+(y+1)^2=5\)
こうして\((-1,-1)\)が中心であり、半径\(\sqrt{5}\)の円軌道を描くとわかりました。
次に\(y=ax-a-2\)を変形すると、\(a(x-1)-2-y=0\)です。つまり、\(y=ax-a-2\)は必ず\((1,-2)\)を通ります。ただ\(a\)の値が何であっても、\(x=1\)の方程式を得られることはありません。つまり、点Pは\((1,0)\)を通ることはありません。
また\(y=bx+3b\)を変形すると、\(b(x+3)-y=0\)です。つまり、\(y=bx+3b\)は必ず\((-3,0)\)を通ります。ただ\(b\)の値が何であっても、\(x=-3\)の方程式を得られることはありません。つまり、点Pは\((-3,-2)\)を通ることはありません。
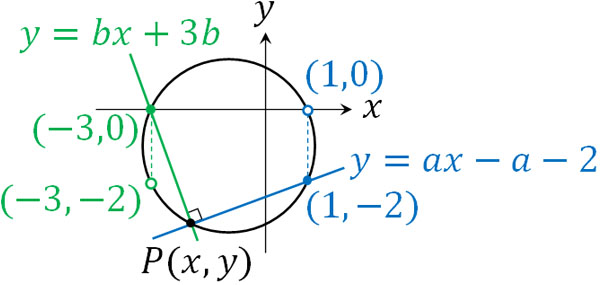
そのため、以下が答えになります。
- \(x^2+y^2+2x+2y-3=0\)、ただし点\((1,0)\)と点\((-3,-2)\)を除く
この問題について、除外点が存在することに気が付くのは難しいです。そこで、図を利用することによって式が条件を満たすかどうか確認しましょう。
放物線と直線による弦の中点の軌道
次に放物線と直線を利用する軌道を計算しましょう。以下の問題の答えは何でしょうか。
- 放物線\(y=x^2\)と直線\(y=m(x+1)\)が異なる2点A,Bで交わります。
- \(m\)の範囲はいくらですか。
- 線分ABの中点の軌道を求めましょう。
1) \(m\)の範囲はいくらですか
交点を計算するため、\(y=x^2\)を\(y=m(x+1)\)に代入しましょう。
\(y=m(x+1)\)
\(x^2=m(x+1)\)
\(x^2-mx-m=0\)
放物線\(y=x^2\)と直線\(y=m(x+1)\)が異なる2点で交わるためには、\(x^2-mx-m=0\)が2つの解をもつ必要があります。そこで、判別式\(D\)を利用することで\(m\)の範囲を計算しましょう。
\((-m)^2-4×-m>0\)
\(m^2+4m>0\)
\(m(m+4)>0\)
こうして、\(m<-4,0<m\)が答えであるとわかります。
2) 線分ABの中点の軌道を求めましょう
\(x^2-mx-m=0\)の答えを得ることができれば、中点の座標を計算できます。解の公式を利用してもいいですが、計算を簡単にするため、解と係数の関係を利用しましょう。2つの解を\(α,β\)とすると、中点は\(\displaystyle\frac{α+β}{2}\)です。
そのため線分ABの中点Pの座標を\((x,y)\)とすると、解と係数の関係より、\(x\)座標は\(\displaystyle\frac{m}{2}\)となります。つまり\(x=\displaystyle\frac{m}{2}\)であり、\(m=2x\)のとき、線分ABの中点を表すことができます。
また、点Pは\(y=m(x+1)\)上にある点です。そのため、\(m=2x\)を\(y=m(x+1)\)に代入しましょう。
\(y=m(x+1)\)
\(y=2x(x+1)\)
\(y=2x^2+2x\)
こうして、\(x\)座標が線分ABの中点である\(\displaystyle\frac{m}{2}\)のとき、\(y=2x^2+2x\)となるとわかりました。
次に、\(x\)の範囲を確認しましょう。\(m=2x\)と\(m<-4,0<m\)を利用して以下のように計算します。
\(m<-4,0<m\)
\(2x<-4,0<2x\)
\(x<-2,0<x\)
こうして、線分ABの軌道は「\(y=2x^2+2x\)について、\(x<-2,0<x\)の部分」とわかりました。
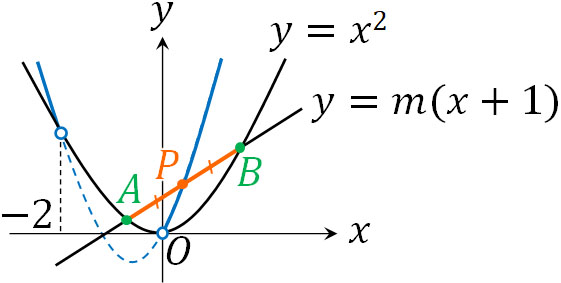
軌道の方程式を求めるとき、条件を利用することで計算しましょう。このとき今回の問題のように、除外点ではなく、特定の範囲を含まないケースがあることを理解しましょう。
条件を利用し、軌道の方程式を計算する
点が動くとき、軌道を描きます。そこで、点が描く軌道を計算できるようになりましょう。軌道を計算できれば、衛星軌道や空中での物体の動きなど、さまざまな現象を数式で表せるようになります。
どのような軌道を描くのかについて、曲線になることがあれば、直線になることもあります。また軌道が曲線を描くとき、円を描くことがあれば、放物線を描くこともあります。このとき、除外点が存在するケースがあることに注意しましょう。
軌道の計算では、求めたい軌道の点を\((x,y)\)に設定しましょう。そうして条件をもとに計算し、軌道の方程式を得ます。
軌道の計算では正しい手順があります。そこでさまざまな練習問題を解き、曲線や直線の軌道を計算できるようになりましょう。