複数候補の中から選んだあと、順番に並べるのが順列です。順列の公式を利用することによって、何通りの方法があるのか数えることができます。
ただ順列の中には、特殊な順列があります。それが円順列・じゅず順列と重複順列です。順列の公式を利用して計算することになるものの、計算方法が一般的な順列とは異なります。つまり、計算方法を理解しないといけません。
また公式を利用できるだけでなく、実際の問題を解けるようになる必要があります。表と裏、組み分け(グループの区別)など、問題の解き方を理解しなければいけません。
解き方を理解していないと円順列やじゅず順列、重複順列の答えを出すのは難しいです。そこで、どのように特殊な順列の答えを出せばいいのか解説していきます。
もくじ
円を利用して並べる場合の順列
特殊な順列に円順列があります。円順列では、円形にて順番に並べます。一般的な順列では、一直線上に並べます。そうではなく、円順列では円形になるのです。
一般的な順列と同じように計算すると、円順列では困ることがあります。以下のように座る場所が一つずつずれる場合、同じ配置になります。
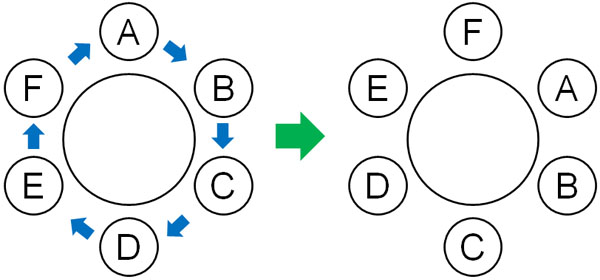
順列では、異なる並びかたを数えなければいけません。そのため回転させて同じ配置になる場合、同じものと考え、排除しなければいけません。
一つを固定し、順列を考える
それでは、どのように円順列の計算をすればいいのでしょうか。円順列の計算をするとき、一つを固定しましょう。例えば以下のように、Aを固定するのです。
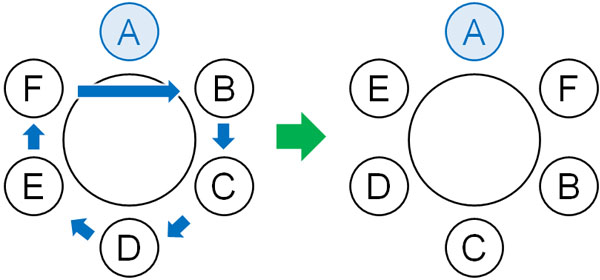
一つの位置を固定すれば、ほかの部分の配置換えをするとき、同じ並び順になることはありません。そのため円順列を解くとき、必ず一カ所を固定しましょう。
例えば6人を円形に並べるとき、何通りの方法があるでしょうか。一列に並べる場合、6!通りの方法があります。ただ円順列では、前述の通り一人を固定します。つまり残り五人で順列を考えなければいけません。そのため以下の計算になります。
- \((6-1)!=5!=120\)
こうして120通り(5!通り)の方法があると計算できます。
この考え方を学べば、円順列の公式を理解できます。一列に並べる順列では\(n!=_nP_n\)という公式を利用します。一方で円順列では、一個(または一人)を排除した後に順列を計算しなければいけません。そのため、以下の公式になります。
- \((n-1)!\)
なお、この公式を覚える必要はありません。円順列では一ヵ所を固定すればいいので、円順列の計算をするときに一個分を除外して順列の計算をすればいいとわかります。
問題の解き方は一般的な順列と同じ
なお、円順列の解き方は一般的な順列の場合と同じです。円順列では一ヵ所を固定する必要があるものの、それ以外は一列に並べる順列の考え方と変わりがありません。例えば、以下の問題はどのように解けばいいでしょうか。
- 男性が5人、女性が3人いて円形のテーブルに座ります。女性の隣に必ず男性が座る場合、何通りの方法がありますか?
円順列であるため、一人を固定しましょう。男性は5人であるため、円順列では\((5-1)=4\)人の男性を利用して円順列を計算します。そうすると、男性の並びかたには4!通りの方法があるとわかります。
- \(4!=4×3×2=24\)
また男性の間に女性が座ります。女性が座れる場所は5カ所であり、ここに3人が座れます。
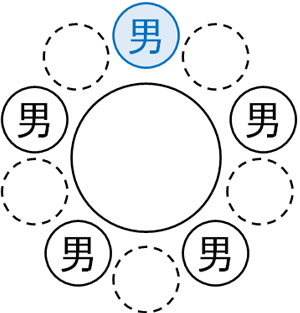
5つの候補から3つを選ぶため、並びかたは5P3です。
- \(_5P_3=5×4×3=60\)
そのため、答えは以下になります。
- \(24×60=1440\)
実際に円順列の問題を解くとき、「一ヵ所を固定する以外、一般的な順列の計算方法と同じ」と理解できます。そのため一般的な順列の計算ができる場合、円順列の問題を解くのは難しくありません。
表と裏がある場合、じゅず順列になる
なお円順列の一種であり、より特殊な順列にじゅず順列があります。円順列との違いとして、じゅず順列では表と裏があります。
人を円形のテーブルに並べるとき、表と裏はありません。一方でネックレスを作る場合、表と裏があります。そのためネックレスを裏返しにする場合、以下は同じ並び順と考えることができます。
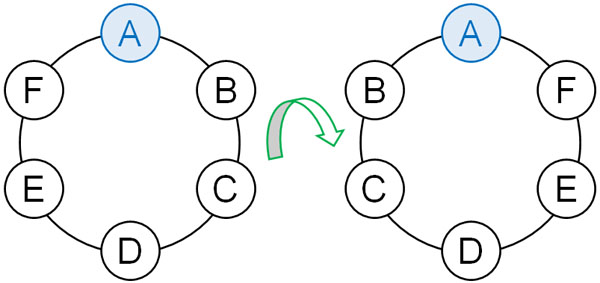
このように表と裏をもつ場合、じゅず順列と判断できます。じゅず順列の場合、一ヵ所を固定するだけでは不十分であり、表と裏を考慮しなければいけません。
ただじゅず順列の計算方法は簡単であり、このときは円順列の結果に対して2で割るようにしましょう。じゅず順列について、円順列との違いは前述の通り「表と裏がある」ことです。表と裏の2パターンがあるため、裏返しにするときに同じになることを考慮して半分にするのです。
つまり、じゅず順列の公式は以下になります。
- \(\displaystyle\frac{(n-1)!}{2}\)
じゅず順列を計算するとき、最初に円順列を計算した後、2で割りましょう。ネックレスや腕輪、ブレスレットなど、裏返しにできる場合はじゅず順列です。
重複順列では、何度も選ぶことができる
特殊な順列には重複順列もあります。一般的な順列では、一つの要素を利用すると、再び利用することができません。そのため階乗を計算するとき、一つずつ数を減らしてかけ算をします。
一方で重複順列では、同じ要素を何度も利用することができます。例えば、以下の問題の答えは何でしょうか。
- 1~6の番号が書かれているカードを利用し、3ケタの数字を作ります。同じカードを何度も使っていい場合、何通りの方法がありますか?
同じカードを何度も利用することができるため、百の位や十の位、一の位にはそれぞれ6つの候補があります。そのため、以下の計算式になります。
- \(6×6×6=216\)
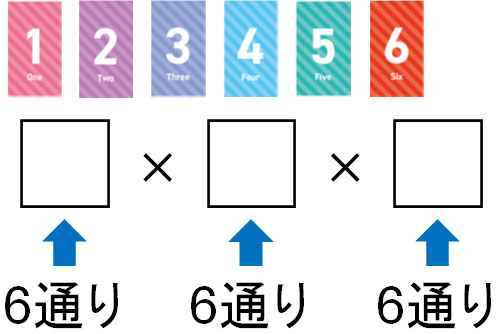
何度も使えるため、階乗のように数字が減ることなく、かけ算をします。重複ありにて、n個の候補からr回を取り出す場合、以下のように重複順列を計算することができます。
- \(n^r\)
なお公式を覚えても利用できることはないため、重複順列が何を意味するのか理解しましょう。そうすれば、公式なしに重複順列を計算できます。
それでは、実際に重複順列の問題を解いてみましょう。以下の答えは何でしょうか。
- A、B、C、D、Eの5人をXグループまたはYグループに分けます。何通りの方法がありますか?
5人がいて、XグループまたはYグループに入ります。それぞれの人についてXまたはYの2通りの方法があり、以下の図を作ることができます。
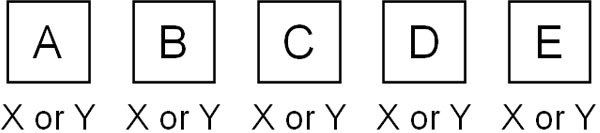
2通りの方法(XまたはY)があり、6回繰り返すことになるため、以下の重複順列の式を作ることができます。
- \(2^6=64\)
重複順列を解くとき、図を作ると理解しやすいです。同じ要素を何度も利用できる場合は重複順列なので、累乗を利用することで計算しましょう。
重複順列での組み分け(グループの区別)の問題
なお重複順列では、条件を与えられることがあります。例えば、以下の問題の答えは何でしょうか。
- A、B、C、D、Eの5人をXグループまたはYグループに分けます。必ずどちらかのグループに人が入れられる場合、何通りの方法がありますか?
先ほどの答えでは、「Xグループに全員が入る」「Yグループに全員が入る」というケースがあります。そのためこの問題を解くとき、一つのグループに全員が入るケースを排除しなければいけません。
一つのグループに全員が入るケースは2パターンです。そこで全体(64通り)から2パターン(XまたはYに全員が入るケース)を引きましょう。そうすると、答えは\(64-2=62\)通りであるとわかります。
・分けるとき、グループを区別しない場合の考え方
重複順列には、ほかにも理解しなければいけないことがあります。先ほど、XグループとYグループに分けて人が入る場面を考えました。それではXグループとYグループを考慮せず、単に2つのグループへ分ける場合を考えるのです。
例えば、以下の問題の答えは何でしょうか。
- A、B、C、D、Eの5人を2つのグループに分けます。何通りの方法がありますか?
先ほどと異なり、XやYのようにグループを区別しません。そのため、例えば「A-B-C, D-E」の分け方と「D-E, A-B-C」の分け方は同じです。

2つのグループを明確に区別する場合、別のものと考えなければいけません。ただグループを区別しない場合、両方は同じものと考えます。2グループは同じであるため、グループには2!通りの方法があります。そこで\(2!=2\)で割りましょう。
- \(\displaystyle\frac{2^6}{2}=\displaystyle\frac{64}{2}=32\)
こうして、32通りの方法があるとわかります。
参考までに3つのグループに分ける場合、3つのグループは3!通りのパターンがあります。そのため3グループを区別しない場合、\(3!=3×2=6\)で割ります。どの数字で割るのかについては、見分けることができないグループの数で決まります。
重複順列を計算するとき、0個(または0人)のグループがあっても問題ないのかどうかを確認しましょう。また、グループを区別するのかどうかも確認しましょう。これらの条件があるのかないのかによって、答えの出し方が変わります。
円順列、じゅず順列、重複順列の計算を行う
順列の計算ではあるものの、特殊な順列として円順列やじゅず順列、重複順列が知られています。一般的な順列と比べて、これらの順列では計算方法が異なります。
円順列を計算する場合、必ず一ヵ所を固定しましょう。これにより、一般的な順列と計算方法が同じになります。また表と裏があり、裏返しにできる場合はじゅず順列を利用します。じゅず順列では、2で割る必要があります。
また、同じ要素を何度も選べる場合は重複順列になります。重複順列では累乗を利用して計算しましょう。また重複順列では条件を加えられることが頻繁にあるため、条件を考慮して答えを出さなければいけません。
解き方を理解していないと、円順列やじゅず順列、重複順列の答えを得ることはできません。そこで計算方法を事前に理解しましょう。






