群数列：初項や和、一般項の計算、分数を含む群数列の解き方

特殊な数列に群数列があります。群として数列を区切ることにより、数列の中に新たな数列が生まれる場合、それを群数列といいます。

群数列では、問題の解き方が決まっています。そのため解き方を知っていれば、答えを得ることができます。一方で、解き方を知らなければ問題を解くことはできません。

また群数列を学ぶとき、文章を読んでも理解するのは難しいです。そこで練習問題を解くことにより、どのように答えを得ればいいのか学びましょう。群数列の問題の解き方を解説していきます。

1 区切ることで新たな数列ができる群数列
2 分数を含む群数列の計算問題
- 2.1 第\(n\)群の総和を計算し、答えを得る
3 群数列の解き方を学ぶ

区切ることで新たな数列ができる群数列

数列では、規則性をもって数字が羅列されることになります。このとき、群として数列を区切ることにより、新たな数列が生まれます。例として、以下の奇数の数列を考えましょう。

\(1,3,5,7,9,11\)\(,13,15\)\(,17,19\)\(,21,…\)

ここで、以下のように数列を区切りましょう。

\(1|3,5|7,9,11\)\(|13,15\)\(,17,19\)\(|21,…\)

このように区切ることにより、新たな数列が生まれます。また、それぞれの区切りを群といいます。

例えば、9はどのような数字でしょうか。数列全体では、9は左から5番目に存在するため、9は第5項です。一方で群で考えると、9は第3群の左から2番目に存在することになります。

これが群数列の概要です。なお群数列では、「特定の数字について第何群に存在するのか」「群に存在する数の総和はいくらか」などを計算することになります。

第\(n\)群の最初の数字を得る

それでは、実際に群数列の問題を解いてみましょう。先ほど記したように、奇数の数列について、第\(n\)群が\(n\)個の数を含むように分けます。

\(1|3,5|7,9,11\)\(|13,15\)\(,17,19\)\(|21,…\)

このとき、第\(n\)群の最初の数はなんでしょうか。

元の数列と群数列で文字が重なると、計算ミスが起こります。そこで、元の数列を利用して計算するときと、群数列を利用して計算するときでは利用する文字を分けましょう。ここでは、元の数列の計算では\(k\)を利用して計算します。

・数列の一般項を得る

元の数列は初項1、公差2の等差数列です。そのため第\(k\)項の式（一般項）は\(2k-1\)です。

・群数列で項の数を計算する

次に、群数列を利用して奇数の数を計算しましょう。\(n\)群を調べたいとき、\(n-1\)群までに含まれる奇数（項）の個数を調べればいいとわかります。\(n-1\)群までに含まれる奇数の個数に対して1を加えると、「第\(n\)群の最初の数字が元の数列で何番目に存在するのか」がわかります。

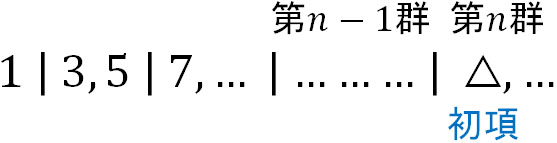
第\(n\)群は\(n\)個の数を含むため、第\(n-1\)群は\(n-1\)個の数を含みます。そこで、第1群から第\(n-1\)群までに存在する奇数の個数を計算しましょう。

\(1+2+3+…+n-1\)

\(=\displaystyle\sum_{k=1}^{n-1}{k}\)

\(=\displaystyle\frac{1}{2}(n-1)n\)

第1群から第\(n-1\)群までに\(\displaystyle\frac{1}{2}(n-1)n\)個の奇数が存在します。そのため、第\(n\)群の最初の奇数は元の数列で\(\displaystyle\frac{1}{2}(n-1)n+1\)番目に存在します。

先ほど計算した通り、\(k\)番目に存在する数字を得るには、一般項\(2k-1\)へ代入すればいいです。そこで、\(\displaystyle\frac{1}{2}(n-1)n+1\)を\(2k-1\)へ代入しましょう。

\(2k-1\)

\(=2\left\{\displaystyle\frac{1}{2}(n-1)n+1\right\}-1\)

\(=(n-1)n+2-1\)

\(=n^2-n+1\)

こうして、第\(n\)群の最初の数を得ることができました。このように群数列の計算では、元の数列と群の両方の性質を利用して計算することになります。

第\(n\)群の総和を計算する

次に、第\(n\)群の総和を計算しましょう。第\(n\)群だけに着目すると、一つの数列になっているとわかります。

先ほど計算した通り、第\(n\)群の最初の数は\(n^2-n+1\)です。また、公差は2です。第\(n\)群には、\(n\)個の奇数が存在することもわかっています。つまり、第\(n\)群に含まれる奇数は以下の条件を満たす等差数列であるとわかります。

初項：\(n^2-n+1\)
公差：2
項数：\(n\)

初項\(a\)、公差\(d\)、項数\(n\)の等差数列の和\(S_n\)は以下の公式によって得ることができます。

\(S_n=\displaystyle\frac{1}{2}n\{2a+(n-1)d\}\)

そこで、この公式へ代入しましょう。

\(S_n=\displaystyle\frac{1}{2}n\{2(n^2-n+1)+(n-1)2\}\)

\(S_n=\displaystyle\frac{1}{2}n×2n^2\)

\(S_n=n^3\)

こうして、第\(n\)群の総和を計算することができました。

特定の数の場所を求める

それでは特定の数について、第何群の何番目に存在するのか計算できるようになりましょう。先ほどの奇数の数列について、101は第何群の何番目に存在するでしょうか。101が第\(n\)群の\(m\)番目に存在すると考えて計算しましょう。

第\(n\)群の初項は\(n^2-n+1\)です。つまり、101は\(n^2-n+1≦101\)の条件を満たします。また第\(n+1\)群の初項は\((n+1)^2-(n+1)+1\)です。\((n+1)^2-(n+1)+1\)は以下のように計算できます。

\((n+1)^2-(n+1)+1\)

\(=n^2+2n+1-n\)

\(=n^2+n+1\)

101は第\(n+1\)群の初項よりも小さい値であるため、\(101<n^2+n+1\)です。そこで、以下の不等式を作りましょう。

\(n^2-n+1≦101\)\(<n^2+n+1\)

\(n^2-n≦100\)\(<n^2+n\)

\(n(n-1)≦100\)\(<n(n+1)\)

\(n=10\)のとき、\(9×10=90\)、\(10×11=110\)となり、101は第10群に存在するとわかります。そこで、第10群の初項を計算しましょう。

\(=10^2-10+1\)

\(=91\)

第10群は初項91、公差2の等差数列です。そのため第10群の\(m\)番目に101が存在する場合、以下の式を作ることができます。

\(101=91+(m-1)·2\)

\(101=91+2m-2\)

\(2m=12\)

\(m=6\)

こうして、101は第10群の6番目に存在するとわかりました。

分数を含む群数列の計算問題

次に、分数を含む場合の群数列の計算問題を解いてみましょう。分数が存在する場合、分子と分母の規則性を分けて考えると答えを得ることができます。

それでは以下の数列について、第1項から第210項までの和を求めましょう。

\(\displaystyle\frac{1}{1},\displaystyle\frac{2}{2},\displaystyle\frac{3}{2},\displaystyle\frac{4}{3},\displaystyle\frac{5}{3},\displaystyle\frac{6}{3},\)\(\displaystyle\frac{7}{4},\displaystyle\frac{8}{4},\)\(\displaystyle\frac{9}{4},\displaystyle\frac{10}{4},\)\(\displaystyle\frac{11}{5},…\)

分母に着目することで、以下のように区切ります。

\(\displaystyle\frac{1}{1}|\displaystyle\frac{2}{2},\displaystyle\frac{3}{2}|\displaystyle\frac{4}{3},\displaystyle\frac{5}{3},\displaystyle\frac{6}{3}|\)\(\displaystyle\frac{7}{4},\displaystyle\frac{8}{4},\)\(\displaystyle\frac{9}{4},\displaystyle\frac{10}{4}|\)\(\displaystyle\frac{11}{5},…\)

このように区切ると、第\(n\)群には\(n\)個の数が含まれているとわかります。そのため、第1群から第\(n\)群までの項数は以下のようになります。

\(1+2+3+…+n\)

\(=\displaystyle\sum_{k=1}^{n}{k}\)

\(=\displaystyle\frac{1}{2}n(n+1)\)

それでは、第210項は第何群に含まれるのでしょうか。第210項が第\(n\)群に含まれると考えると、210は第\(n-1\)群までの項数より大きく、第\(n\)群までの項数以下となります。つまり、以下の式を作れます。

\(\displaystyle\frac{1}{2}(n-1)n<210\)\(≦\displaystyle\frac{1}{2}n(n+1)\)

\((n-1)n<420\)\(≦n(n+1)\)

\(n=20\)のとき、\(19×20=380\)です。また、\(20×21=420\)です。そのため、第210項は第20群に存在するとわかります。

第\(n\)群の総和を計算し、答えを得る

次に、第\(n\)群の総和を計算しましょう。先ほど計算した通り、\(20×21=420\)であるため、第210項は第20群の最後の数です。そこで、まずは第\(n\)群の総和を計算しましょう。

第\(n\)群の総和を得るため、第\(n\)群の初項を計算します。元の数列に着目すると、第\(k\)項の場合、分子は初項1、公差1の公差数列です。そのため、第\(k\)項の分子は\(k\)です。

なお、第1群から第\(n-1\)群までの項数は\(\displaystyle\frac{1}{2}(n-1)n\)です。そのため、第\(n\)群の初項の項数は\(\displaystyle\frac{1}{2}(n-1)n+1\)です。そのため、初項の分子の値は\(\displaystyle\frac{1}{2}(n-1)n+1\)です。

そこで分子だけに着目すると、第\(n\)群では、初項\(\displaystyle\frac{1}{2}(n-1)n+1\)、公差1、項数\(n\)の等差数列です。そこで、以下のように第\(n\)群での分子の和\(S\)を計算します。

\(S=\displaystyle\frac{1}{2}n\{2a+(n-1)d\}\)

\(S=\displaystyle\frac{1}{2}n\{(n-1)n+2+(n-1)·1\}\)

\(S=\displaystyle\frac{1}{2}n(n^2-n+2+n-1)\)

\(S=\displaystyle\frac{1}{2}n(n^2+1)\)

こうして第\(n\)群では、分子の総和は\(\displaystyle\frac{1}{2}n(n^2+1)\)とわかりました。なお第\(n\)群の分母は\(n\)であるため、\(n\)で割ると、第\(n\)群の総和を計算できます。つまり、\(\displaystyle\frac{n^2+1}{2}\)が第\(n\)群の総和です。

それでは第\(n\)群の総和ではなく、第1群から第\(n\)群の総和を計算しましょう。以下の式によって第1群から第\(n\)群の総和を計算できます。

\(\displaystyle\sum_{k=1}^{n}{\displaystyle\frac{k^2+1}{2}}\)

\(=\displaystyle\frac{1}{2}\displaystyle\sum_{k=1}^{n}{(k^2+1)}\)

\(=\displaystyle\frac{1}{2}·\displaystyle\frac{1}{6}n(n+1)(2n+1)\)\(+\displaystyle\frac{1}{2}n\)

先ほど計算した通り、\(n=20\)であるため、この式に代入しましょう。

\(\displaystyle\frac{1}{2}·\displaystyle\frac{20×21×41}{6}\)\(+\displaystyle\frac{1}{2}×20\)

\(=1435+10\)

\(=1445\)

こうして、第1群から第20群までの総和（第1項から第210項までの和）を得ることができました。分数を含む群数列であっても、問題の解き方は同じであるとわかります。