確率の計算をするとき、かけ算や足し算をすることによって答えを出します。このとき場合によっては、異なる操作を同時に行うことがあります。この場合は独立な試行として、かけ算を利用することによって計算します。
他には、同じ操作を繰り返すこともあります。この場合は反復試行と呼ばれ、反復試行の確率を計算するときは組み合わせを利用することによって確率を計算しなければいけません。
これら独立な試行の確率と反復試行の確率を理解したら、応用問題を解けるようになりましょう。確率の問題では、応用問題は難しいです。そこで基本となる問題を理解し、さまざまなパターンの問題を解く必要があります。
公式を覚えても確率の問題を解けるようにはなりません。問題のパターンと解き方を覚えることによって、答えを出せるようになります。そこで、どのように独立な試行の確率と反復試行の確率を計算すればいいのか解説していきます。
もくじ
独立な試行では、かけ算によって確率を計算する
確率の計算では、独立な試行を求めなければいけないことがよくあります。このとき独立な試行とは何でしょうか。2つの試行をするとき、互いに影響しないときは独立な試行といいます。
例えば、以下の問題の答えは何でしょうか。
- Aの袋には赤玉4つと青玉4つが入っており、Bの袋には赤玉3つと青玉5つが入っています。袋Aから1つ、袋Bから2つ玉を取り出すとき、すべて赤玉の確率を求めましょう。
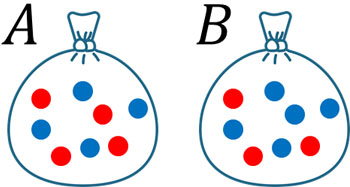
袋Aから1つの玉を取り出すため、赤玉となる確率は\(\displaystyle\frac{4}{8}=\displaystyle\frac{1}{2}\)です。またBから2つの玉を取り出し、両方とも赤玉になる確率は以下のようになります。
\(\displaystyle\frac{_3C_2}{_8C_2}=\displaystyle\frac{3}{28}\)
こうして袋Aと袋Bについて、赤玉を取り出す確率をそれぞれ計算することができました。それでは袋Aと袋Bについて、すべて赤玉になる確率は何でしょうか。
袋Aから球を取り出す作業と袋Bから球を取り出す作業は独立であり、まったく別の作業です。そのため、2つのイベント(袋Aと袋Bについて、両方とも赤玉を取り出すイベント)が同時に起こる確率を得るためにはかけ算をすればいいとわかります。
確率の計算では、2つの事象が同時に起こるとき、かけ算をすることによって計算します。例えば2つのサイコロを投げるとき、2つとも1の目が出る確率は\(\displaystyle\frac{1}{6}×\displaystyle\frac{1}{6}=\displaystyle\frac{1}{36}\)になります。これと同じように計算すると、先ほどの問題の答えは以下のようになります。
\(\displaystyle\frac{1}{2}×\displaystyle\frac{3}{28}=\displaystyle\frac{3}{56}\)
このように独立な試行では、かけ算を利用することによって計算しましょう。
三回や四回の試行でも、独立しているならかけ算を利用
なお独立な試行について、先ほどは2つの事象について確率を計算しました。それでは、独立な試行を3回や4回する場合はどのようになるのでしょうか。
このときも考え方は同じであり、独立な試行なのであれば、かけ算を利用しましょう。例えば独立な試行を三回するのであれば、3つの要素をすべてかけます。また独立な試行を四回するのであれば、4つの要素をすべてかけます。
独立な試行をする場合、それぞれの要素について起こる確率を計算し、かけ算をすることによって答えを出すことができます。
排反事象の場合、加法定理を利用して足し算をする
このように独立な試行の確率を計算することによって、一つのイベントが起こる確率を計算することができます。なお確率の計算をするときに、まったく異なる結果が発生する場合、今度は足し算をすることによって答えを出しましょう。
異なる結果のとき、それらの事象を排反事象といいます。排反事象の計算を理解するため、以下の問題を解いてみましょう。
- Aの袋には赤玉4つと青玉4つが入っており、Bの袋には赤玉3つと青玉5つが入っています。袋Aから1つ、袋Bから2つ玉を取り出すとき、すべての玉が同じ色になる確率を求めましょう。

先ほどの問題と似ています。ただすべての玉が同じ色になる場合というのは、すべて赤色のケースだけでなく、すべて青色のケースもあります。「すべて赤色」と「すべて青色」はまったく異なる結果です。そのため排反事象であり、足し算を利用することによって確率を計算しましょう。
すべて赤玉となる確率は先ほど計算した通り\(\displaystyle\frac{3}{56}\)です。またすべて青玉となる確率は以下の式によって計算できます。
\(\displaystyle\frac{1}{2}×\displaystyle\frac{_5C_2}{_8C_2}=\displaystyle\frac{5}{28}\)
そこですべて同じ色の玉になる確率を計算するため、「すべて赤色の確率」と「すべて青色の確率」について、以下のように足しましょう。
\(\displaystyle\frac{3}{56}+\displaystyle\frac{5}{28}=\displaystyle\frac{13}{56}\)
こうして、答えを得ることができます。
反復試行の確率は組み合わせを利用する
なお確率の計算では、同じことを何度も繰り返す問題も出題されます。例えば先ほどの問題では、袋から玉を取り出した後、同じ玉を利用することはしません。一方で玉を取り出して確認した後、袋に戻す場合があるのです。
この場合は反復試行といいます。同じ操作を繰り返すことになるため、先ほどとは確率の計算方法が異なります。かけ算を利用して確率を計算するのは同じであるものの、違う計算方法になると理解しましょう。
具体的には、組み合わせを利用することによって反復試行の確率を計算します。例えば、以下の問題の答えは何でしょうか。
- サイコロを5回投げ、4の目が2回出る確率を求めましょう。
サイコロを投げるとき、出る目の条件は常に同じです。そのため同じ作業を繰り返す反復試行です。このとき、サイコロには1~6の数字があるため、4の目が出る確率は\(\displaystyle\frac{1}{6}\)です。一方で4以外の目が出る確率は\(\displaystyle\frac{5}{6}\)です。
「4が2回、4以外が3回」となる必要があるため、以下のようにかけ算をしましょう。
\(\left(\displaystyle\frac{1}{6}\right)^2\left(\displaystyle\frac{5}{6}\right)^3\)
ただ以下のように、4の目が出るタイミングはそれぞれ異なります。
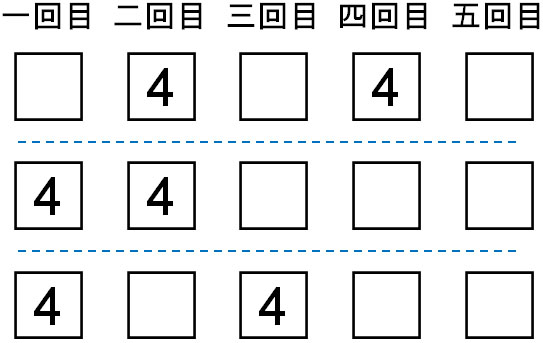
つまりサイコロを5回投げ、そのうち4が出る部分を2つ選ぶ必要があります。そこで、組み合わせを利用しましょう。以下の式を作ることによって、4が2回出る確率を計算することができます。
\(_5C_2\left(\displaystyle\frac{1}{6}\right)^2\left(\displaystyle\frac{5}{6}\right)^3=\displaystyle\frac{625}{3888}\)
このように「組み合わせ」「特定の事象が出る確率」「特定の事象が出ない確率」を利用することによって、反復試行の確率が計算できるようになります。
順列ではなく、組み合わせを用いる理由
反復試行の確率というのは、同じ条件で独立な試行を何度も繰り返すときの確率です。このとき、なぜ順列ではなく組み合わせを利用するのか理解できない人がいるかもしれません。この理由として、反復試行では順番を考慮しないからです。
順列では順番が重要になります。一方で組み合わせでは、並び順を考慮しません。先ほどの問題では、5つのうち2つをランダムに選び、選んだ場所に4を入れます。2つの場所に4を入れるとき、2ヵ所にある4は同じ数字であるため区別できません。
反復試行では、同じ操作を繰り返すことになります。そのため同じ結果が出るとき、それらを区別することができないのです。そのため順列ではなく、組み合わせを利用するというわけです。
なお反復試行の確率を計算するとき、以下の公式を利用します。
- \(_nC_rP^r(1-P)^{n-r}\)
ただ、この公式を覚えても意味がありません。そこで公式を覚えるのではなく、「どのようにして反復試行の確率を計算すればいいのか」の方法を理解し、式を作れるようにしましょう。そうすれば、公式なしに計算できるようになります。
応用問題では答えを出すために必要な条件を考える
反復試行の確率を計算する方法を理解した後、応用問題を解けるようになりましょう。反復試行の確率に関する応用問題は難しく、多くのパターンがあります。
反復試行の確率では、解き方を理解していないと、応用問題を解けないことが多いです。そこで多くの問題を解き、どのような問題が出されても解けるようになりましょう。
例えば、以下の問題の答えは何でしょうか。
- AとBが決勝戦をします。先に3回勝つと優勝であり、引き分けはありません。またAが勝つ確率は\(\displaystyle\frac{2}{3}\)です。Aが3連勝する確率と6試合目にAが優勝する確率を求めましょう。
Aが優勝するとき、3連勝するのか、それとも3勝2敗になるのかによって確率が異なります。そこで、以下のように確率を計算しましょう。
・Aが3連勝する場合
Aが勝つ確率は\(\displaystyle\frac{2}{3}\)です。そのため、Aが3連勝する確率は以下になります。
\(\left(\displaystyle\frac{2}{3}\right)^3=\displaystyle\frac{8}{27}\)
・Aが3勝2敗で優勝する場合
確率の計算をするとき、「Aが3回勝てばいい」と考えて以下の式を作るのは誤答です。
\(_5C_3\left(\displaystyle\frac{2}{3}\right)^3\left(\displaystyle\frac{1}{3}\right)^2\)
なぜこの式が間違いかというと、Aが3勝2敗で優勝するためには、その前が2勝2敗である必要があるからです。先ほどの式であれば、以下のように5回試合をして、Aが最初の3回を勝つケースも含まれてしまいます。

ただ実際には、3連勝するとAの優勝が決定するため、このケースを含むのは間違いです。そこで2勝2敗になる確率を計算し、そのあとにAが勝って3勝2敗になる確率を出しましょう。
2勝2敗になる確率は以下のようになります。
\(_4C_2\left(\displaystyle\frac{2}{3}\right)^2\left(\displaystyle\frac{1}{3}\right)^2\)
そこで以下の式によって、Aが勝って3勝2敗になる確率を計算しましょう。
\(_4C_2\left(\displaystyle\frac{2}{3}\right)^2\left(\displaystyle\frac{1}{3}\right)^2×\displaystyle\frac{2}{3}=\displaystyle\frac{16}{81}\)
このように、答えを出すためにはどのような条件となるのか考えるようにしましょう。
解き方を理解していないと誤答するケースは多い
また前述の通り、応用問題では解き方を理解していないと誤答するケースが非常に多いです。この記事ではすべてのパターンを記すことはしないため、練習問題を解くことによってさまざまなパターンの計算に慣れなければいけません。
どのようなケースで誤答が起こるのでしょうか。例えば、以下の問題は非常に誤答が多い問題の一つです。
- 下図のような格子状の道路があります。点Aをスタートし、右または上へ\(\displaystyle\frac{1}{2}\)の確率で進み、Cに到着します。このときBを経由してCへ到着する確率を求めましょう。
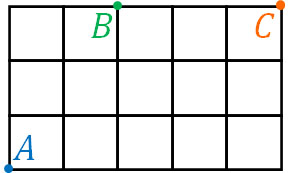
上に3回、右に5回進むことによってCに到着します。そのため確率を計算するとき、「A→B→Cへ行く事象の数(\(_5C_3\))」と「A→Cへ行く事象の数(\(_8C_3\))」を利用し、多くの人は以下のように確率を計算します。
\(\displaystyle\frac{_5C_3}{_8C_3}\)
ただ、この答えは間違いです。なぜ、この計算が誤答なのでしょうか。それは、起こる事象の確率が異なるからです。言い換えると、特定の事象が発生する確率が途中で変化するのです。
例えばサイコロを5回投げるとき、1の目が3回出る確率を計算するとします。このとき途中で以下のようにサイコロの形を変えると、正しく計算することができません。
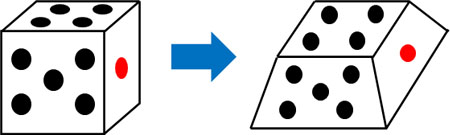
起こる確率が途中で変わる場合、同様に確からしくないといえます。事実、先ほどの問題では道順によって確率が異なります。例えば、以下の道順となる確率はいくらでしょうか。
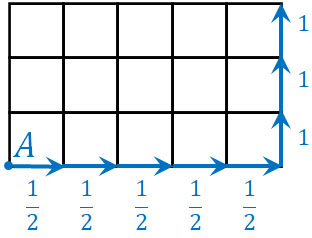
道路の右端に行った後、上に行く確率は100%です。そのため、この道順になる確率は以下のようになります。
\(\left(\displaystyle\frac{1}{2}\right)^5=\displaystyle\frac{1}{32}\)
一方、以下の道順となる確率はいくらでしょうか。
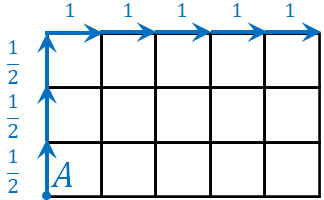
上に行く確率は\(\displaystyle\frac{1}{2}\)です。ただ3回上に行った後、右に行く確率は100%です。そのため、この道順となる確率は以下のようになります。
\(\left(\displaystyle\frac{1}{2}\right)^3=\displaystyle\frac{1}{8}\)
道順によって確率が異なりますし、途中で確率が\(\displaystyle\frac{1}{2}\)ではなく1に変わります。すべての事象について、\(\displaystyle\frac{1}{2}\)の確率で発生するわけではありません。そのため、\(\displaystyle\frac{_5C_3}{_8C_3}\)で計算するのは誤答になるのです。
ただ実際のところ、この事実を理解していない場合、ほとんどの人が誤答します。そのため、多くの練習問題を解くことが重要というわけです。
それでは、先ほどの問題はどのように解けばいいのでしょうか。以下の場所について、記号を振りましょう。
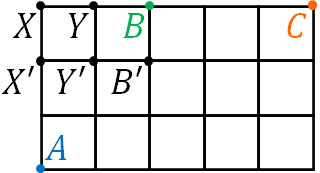
その後、それぞれのパターンについて場合分けをして確率を計算しましょう。
・A→X’→X→Cの道順
上に三回行った後、右に行く確率は100%です。そのため確率は以下のようになります。
\(\left(\displaystyle\frac{1}{2}\right)^3=\displaystyle\frac{1}{8}\)
・A→Y’→Y→Cの道順
A→Y’については、\(\displaystyle\frac{1}{2}\)の確率で上へ二回、右へ一回行くことになります。その後、\(\displaystyle\frac{1}{2}\)の確率で上に行くことでY’→Yとなります。そのため、確率は以下のようになります。
\(_3C_2\left(\displaystyle\frac{1}{2}\right)^2\left(\displaystyle\frac{1}{2}\right)×\displaystyle\frac{1}{2}=\displaystyle\frac{3}{16}\)
・A→B’→B→Cの道順
A→B’については、\(\displaystyle\frac{1}{2}\)の確率で上へ二回、右へ二回行くことになります。その後、\(\displaystyle\frac{1}{2}\)の確率で上に行くことでB’→Bとなります。そのため、確率は以下のようになります。
\(_4C_2\left(\displaystyle\frac{1}{2}\right)^2\left(\displaystyle\frac{1}{2}\right)^2×\displaystyle\frac{1}{2}=\displaystyle\frac{3}{16}\)
こうして、すべての道順についてそれぞれ確率を計算することができました。そこで、先ほど計算した答えをすべて足しましょう。
\(\displaystyle\frac{1}{8}+\displaystyle\frac{3}{16}+\displaystyle\frac{3}{16}=\displaystyle\frac{1}{2}\)
解き方を知っていないと、この問題の答えを出すのは非常に難しいです。反復試行の確率を計算するとき、公式を利用できるだけでなく、多くの問題を解かなければいけない理由がこれになります。
独立な試行の確率と反復試行の確率を計算する
確率の計算をするとき、独立な試行ではかけ算を利用して答えを出しましょう。イベントが起こる確率について、それぞれかけることによって答えを得るのです。
また独立な試行について、同じことを繰り返し行うときは反復試行になります。反復試行では公式があるものの、公式を覚えるのではなく、式の作り方を理解しましょう。
独立な試行でも反復試行でも、応用問題は難しいです。公式を理解しても問題を解けない人が多いのは、どのように公式を利用すればいいのかわかっていないからです。また問題を解くとき、解き方のパターンを理解していないと答えを出せないのも、独立な試行の確率と反復試行の確率の特徴です。
そのため多くの問題を解き、あらゆるパターンについて確率の計算をできるようにしましょう。数学では解き方を覚える必要があります。特に独立な試行の確率と反復試行の確率を計算する場合、解き方を覚えていないと高確率で誤答してしまいます。






