加法定理：公式の証明、2倍角・半角・3倍角の公式

三角関数で学ぶ内容に加法定理があります。角度を足したり引いたりするとき、加法定理を利用すればsinθやcosθ、tanθの値を計算できます。加法定理を利用することにより、例えば\(sin15°\)の値を得られるようになります。

なお、加法定理は2直線のなす角を計算するときにも有効です。この場合、tanθを用いて計算します。

また、加法定理を応用することで2倍角の公式や半角の公式、3倍角の公式を得ることができます。これらの公式を覚えるのではなく、加法定理を用いて公式を導出できるようになりましょう。すべての公式を覚えるのは効率的ではありません。

それでは、どのように加法定理を用いて計算すればいいのでしょうか。また、どのように公式を作ればいいのでしょうか。加法定理を用いて計算問題を解く方法を解説していきます。

1 加法定理による公式と計算方法
- 1.1 加法定理の証明：距離の公式と余弦定理
- 1.2 三角関数の値を加法定理を用いて計算する
2 2直線のなす角とtanの利用
3 2倍角の公式を加法定理を用いて得る
- 3.1 半角の公式と計算方法
- 3.2 3倍角の公式を導出する
4 加法定理を覚え、公式を導出できるようにする

加法定理による公式と計算方法

まず、加法定理の公式を覚えるようにしましょう。加法定理を証明することはできますが、毎回証明するのは現実的ではないため、公式を暗記するのです。覚えるべき公式は以下の2つです。

\(sin(α±β)=sinαcosβ±cosαsinβ\)
\(cos(α±β)=cosαcosβ∓sinαsinβ\)

これらの公式は必ず覚えましょう。

tanθに関する加法定理の公式は作ることができます。以下のように、\(sin(α±β)\)と
\(cos(α±β)\)を利用して式を作りましょう。

\(tan(α±β)=\displaystyle\frac{sin(α±β)}{cos(α±β)}\)

\(tan(α±β)=\displaystyle\frac{sinαcosβ±cosαsinβ}{cosαcosβ∓sinαsinβ}\)

次に、分子と分母を\(cosαcosβ\)で割りましょう。そうすると、以下の公式を得ることができます。

\(tan(α±β)=\displaystyle\frac{tanα±tanβ}{1∓tanαtanβ}\)

\(tan(α±β)\)の加法定理を覚える必要はありません。公式を作れることが重要です。

・加法定理を用いて計算する

それでは、加法定理を用いて計算してみましょう。以下の値は何でしょうか。

\(sin15°\)

次のように計算しましょう。

\(sin15°=sin(45°-30°)\)

\(=sin45°cos30°-cos45°sin30°\)

\(=\displaystyle\frac{1}{\sqrt{2}}·\displaystyle\frac{\sqrt{3}}{2}-\displaystyle\frac{1}{\sqrt{2}}·\displaystyle\frac{1}{2}\)

\(=\displaystyle\frac{\sqrt{3}-1}{2\sqrt{2}}\)

\(=\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}\)

こうして、加法定理を利用することによって値を得ることができました。

加法定理の証明：距離の公式と余弦定理

それでは、加法定理の証明をしてみましょう。必ず理解しなければいけない内容ではなく、読み飛ばしても問題ありません。ただ知識として知っていると、どのように公式を導き出せるのか知ることができるため、数学をより深く学べます。

加法定理の証明では、\(cos(α+β)\)からスタートします。以下の図形を利用しましょう。

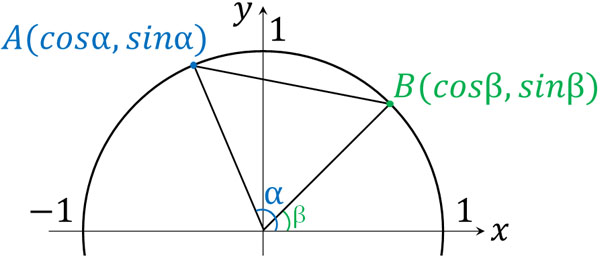
距離の公式を利用して、直線ABの距離の二乗は以下のように計算できます。

\(AB^2=(cosα-cosβ)^2+(sinα-sinβ)^2\)

\(=cos^2α-2cosαcosβ+cos^2β\)\(+sin^2α\)\(-2sinαsinβ\)\(+sin^2β\)

\(=2-2(cosαcosβ+sinαsinβ)\) – ①

次に、余弦定理を利用して以下の計算をしましょう。

\(AB^2=OA^2+OB^2-2OA·OC\)\(·cos(α-β)\)

\(=1^2+1^2-2·1·1·cos(α-β)\)

\(=2-2cos(α-β)\) – ②

①と②より、以下のように計算しましょう。

\(2-2(cosαcosβ+sinαsinβ)\)\(=2-2cos(α-β)\)

\(cos(α-β)=cosαcosβ+sinαsinβ\)

また\(β\)を\(-β\)に置き換えると、以下のようになります。

\(cos(α+β)=cosαcosβ-sinαsinβ\)

こうして、cosθに関する加法定理の証明をすることができました。

なお、cosθでは角度が\(\displaystyle\frac{π}{2}\)（90°）変化すると、cosθはsinθになります。そこで\(α\)を\(\displaystyle\frac{π}{2}-α\)に置き換えましょう。

\(cos\left(\displaystyle\frac{π}{2}-α+β\right)\)\(=cos\left(\displaystyle\frac{π}{2}-α\right)cosβ\)\(-sin\left(\displaystyle\frac{π}{2}-α\right)sinβ\)

\(cos\left(\displaystyle\frac{π}{2}-(α-β)\right)\)\(=cos\left(\displaystyle\frac{π}{2}-α\right)cosβ\)\(-sin\left(\displaystyle\frac{π}{2}-α\right)sinβ\)

\(sin(α-β)=sinαcosβ-cosαsinβ\)

また先ほどと同様に\(β\)を\(-β\)に置き換えると、以下のようになります。

\(sin(α+β)=sinαcosβ+cosαsinβ\)

こうして、三角関数の性質を利用することでsinθについても加法定理の証明をすることができました。

三角関数の値を加法定理を用いて計算する

それでは、加法定理を用いて三角関数の計算をしましょう。以下の問題の答えは何でしょうか。

\(sinα=\displaystyle\frac{4}{5}\)、\(cosβ=\displaystyle\frac{5}{13}\)のとき、\(cos(α-β)\)の値を求めましょう。なお、\(0<α<\displaystyle\frac{π}{2}\)、\(0<β<\displaystyle\frac{π}{2}\)です。

\(cos(α-β)\)の値を計算する必要があるため、加法定理を利用しましょう。ただ加法定理を利用するためには、\(sinβ\)と\(cosα\)の値を知る必要があります。そこで\(sin^2θ+cos^2θ=1\)を利用して、それぞれの値を計算しましょう。

\(0<α<\displaystyle\frac{π}{2}\)より、\(cosα>0\)です。また\(0<β<\displaystyle\frac{π}{2}\)より、\(sinβ>0\)です。次に、公式を利用して以下のように計算します。

・\(cosα\)の計算

\(sin^2α+cos^2α=1\)

\(cosα=\sqrt{1-sin^2α}\)

\(cosα=\displaystyle\frac{3}{5}\)

・\(sinβ\)の計算

\(sin^2β+cos^2β=1\)

\(sinβ=\sqrt{1-cos^2β}\)

\(sinβ=\displaystyle\frac{12}{13}\)

そこで、加法定理を用いて計算しましょう。

\(cos(α-β)=cosαcosβ+sinαsinβ\)

\(cos(α-β)=\displaystyle\frac{3}{5}·\displaystyle\frac{5}{13}+\displaystyle\frac{4}{5}·\displaystyle\frac{12}{13}\)

\(cos(α-β)=\displaystyle\frac{63}{65}\)

こうして、加法定理を利用して計算することができました。

2直線のなす角とtanの利用

2つの角度を利用して計算するとき、加法定理が役立ちます。そこで、加法定理を用いて2直線のなす角を計算してみましょう。

2直線\(x-2y+2=0\)と\(3x-y-3=0\)のなす角を求めましょう。なお、なす角は鋭角です。

2つの直線を変形すると以下のようになります。

\(y=\displaystyle\frac{1}{2}x+1\)
\(y=3x-3\)

下図のように角度を\(α\)、\(β\)とすると、\(tanα\)は直線\(y=3x-3\)の傾きであり、\(tanβ\)は直線\(y=\displaystyle\frac{1}{2}x+1\)の傾きです。そこで\(tanα=3\)、\(tanβ=\displaystyle\frac{1}{2}\)を利用して計算しましょう。

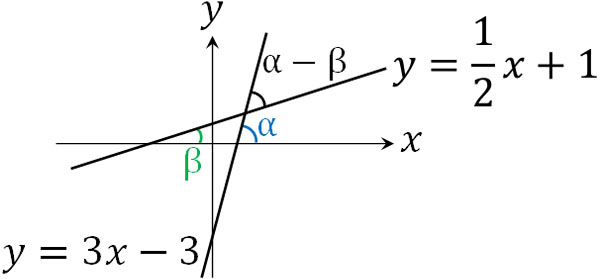
加法定理を利用すると以下のように計算できます。

\(tan(α-β)=\displaystyle\frac{tanα-tanβ}{1+tanαtanβ}\)

\(=\displaystyle\frac{3-\displaystyle\frac{1}{2}}{1+3·\displaystyle\frac{1}{2}}\)

\(=1\)

\(tan(α-β)=1\)であるため、2直線のなす角は\(\displaystyle\frac{π}{4}\)です。

2倍角の公式を加法定理を用いて得る

なお、加法定理の応用として2倍角の公式や半角の公式、3倍角の公式があります。これらの公式を覚えてはいけません。加法定理を利用することにより、2倍角の公式や半角の公式、3倍角の公式を作れるようになりましょう。

角度を倍にするとき、得られる値を計算するための公式が2倍角の公式です。角度を\(α\)とすると、以下が2倍角の公式になります。

\(sin2α=2sinαcosα\)
\(cos2α=cos^2α-sin^2α\)\(=1-2sin^2α\)\(=2cos^2α-1\)
\(tan2α=\displaystyle\frac{2tanα}{1-tan^2α}\)

加法定理で\(β\)を\(α\)に変えれば、2倍角の公式を容易に作ることができます。これが、2倍角の公式を覚えてはいけない理由です。例えば\(sin2α\)の公式を以下のように導出できます。

\(sin(α+α)=sinαcosα+cosαsinα\)

\(sin2α=2sinαcosα\)

\(cosα\)と\(tanα\)についても、同様に公式を作れます。なお、\(sin^2α+cos^2α=1\)であるため、この公式を利用して\(cos2α=cos^2α-sin^2α\)を変形しましょう。そうすれば、ほかの公式を得ることができます。

半角の公式と計算方法

角度を半分にするとき、半角の公式を利用しましょう。倍角の公式を利用することにより、半角の公式を得られます。倍角の公式より、以下のようになります。

\(sin^2α=\displaystyle\frac{1-cos2α}{2}\)
\(cos^2α=\displaystyle\frac{1+cos2α}{2}\)
\(tan^2α=\displaystyle\frac{1-cos2α}{1+cos2α}\)

\(tan^2α=\displaystyle\frac{sin^2α}{cos^2α}\)であるため、値を代入すると上記のようになります。次に、\(α=\displaystyle\frac{θ}{2}\)としましょう。そうすると、以下の公式を導出できます。

\(sin^2\displaystyle\frac{θ}{2}=\displaystyle\frac{1-cosθ}{2}\)
\(cos^2\displaystyle\frac{θ}{2}=\displaystyle\frac{1+cosθ}{2}\)
\(tan^2\displaystyle\frac{θ}{2}=\displaystyle\frac{1-cosθ}{1+cosθ}\)

こうして、半角の公式を得ることができました。

・公式を利用して計算する

それでは、以下の問題を解いてみましょう。

\(\displaystyle\frac{π}{2}<θ<π\)、\(sinθ=\displaystyle\frac{4}{5}\)のとき、\(sin2θ\)、\(cos2θ\)、\(tan\displaystyle\frac{θ}{2}\)の値を求めましょう。

\(sin^2θ+cos^2θ=1\)、\(\displaystyle\frac{π}{2}<θ<π\)であるため、以下のようにcosθを計算できます。

\(cos^2θ=1-sin^2θ\)

\(cos^2θ=\displaystyle\frac{9}{25}\)

\(cosθ=-\displaystyle\frac{3}{5}\)

次に、加法定理を用いて計算しましょう。

・\(sin2θ\)の計算

\(sin2α=2sinαcosα\)

\(sin2α=2·\displaystyle\frac{4}{5}·-\displaystyle\frac{3}{5}\)

\(sin2α=-\displaystyle\frac{24}{25}\)

・\(cos2θ\)の計算

\(cos2θ=1-2sin^2θ\)

\(cos2θ=1-2·\left(\displaystyle\frac{4}{5}\right)^2\)

\(cos2θ=-\displaystyle\frac{7}{25}\)

・\(tan\displaystyle\frac{θ}{2}\)の計算

\(tan^2\displaystyle\frac{θ}{2}=\displaystyle\frac{1-cosθ}{1+cosθ}\)

\(tan^2\displaystyle\frac{θ}{2}=\displaystyle\frac{1-\left(-\displaystyle\frac{3}{5}\right)}{1+\left(-\displaystyle\frac{3}{5}\right)}\)

\(tan^2\displaystyle\frac{θ}{2}=4\)

\(\displaystyle\frac{π}{2}<θ<π\)であるため、\(\displaystyle\frac{π}{4}<\displaystyle\frac{θ}{2}<\displaystyle\frac{π}{2}\)です。つまり、\(tan\displaystyle\frac{θ}{2}>0\)です。そのため、\(tan\displaystyle\frac{θ}{2}=2\)です。

3倍角の公式を導出する

次に3倍角の公式を学びましょう。以下が3倍角の公式になります。

\(sin3α=3sinα-4sin^3α\)
\(cos3α=-3cosα+4cos^3α\)

3倍角の公式についても覚えてはいけません。公式を導出できるようになりましょう。\(3α=2α+α\)と考え、加法定理と2倍角の公式を利用して式を変形するのです。

・\(sin3α=3sinα-4sin^3α\)の導出

\(sin(2α+α)=sin2αcosα+cos2αsinα\)

\(=2sinαcos^2α\)\(+(1-2sin^2α)sinα\)

\(=2sinα(1-sin^2α)\)\(+(1-2sin^2α)sinα\)

\(=3sinα-4sin^3α\)

・\(cos3α=-3cosα+4cos^3α\)の導出

\(cos(2α+α)=cos2αcosα-sin2αsinα\)

\(=(2cos^2α-1)cosα\)\(-2sin^2αcosα\)

\(=(2cos^2α-1)cosα\)\(-2(1-cos^2α)cosα\)

\(=-3cosα+4cos^3α\)

こうして、3倍角の公式を導出できました。それでは、3倍角の公式を利用して問題を解けるようになりましょう。以下の問題の答えは何でしょうか。

\(sin3θ=sinθ\)を満たすθについて、\(0≦θ<2π\)の範囲で求めましょう。

3倍角の公式を利用して以下のように計算しましょう。

\(sin3θ=sinθ\)

\(3sinθ-4sin^3θ=sinθ\)

\(4sin^3θ-2sinθ=0\)

\(sin^3θ-\displaystyle\frac{1}{2}sinθ=0\)

\(sinθ\left(sin^2θ-\displaystyle\frac{1}{2}\right)=0\)

\(sinθ\left(sinθ+\displaystyle\frac{1}{\sqrt{2}}\right)\left(sinθ-\displaystyle\frac{1}{\sqrt{2}}\right)=0\)

\(sinθ=0,±\displaystyle\frac{1}{\sqrt{2}}\)

\(0≦θ<2π\)では、\(θ=0,\displaystyle\frac{π}{4},\displaystyle\frac{3π}{4},π,\displaystyle\frac{5π}{4},\displaystyle\frac{7π}{4}\)が答えです。加法定理を利用して、3倍角の公式についても利用できるようになりましょう。