和の法則と積の法則：高校数学での場合の数

高校数学で学ぶ内容に和の法則と積の法則があります。場合の数を学ぶとき、この法則を習います。ただ和の法則や積の法則というのは、小学算数や中学数学ですでに習っている内容になります。

和の法則では、足し算（または引き算）をすることによって起こる個数を数えます。また積の法則を利用する場合、掛け算によって起こる個数を計算できます。両方とも樹形図が有効であり、和の法則も積の法則でも樹形図が利用されます。

小学算数や中学数学に比べて問題文は難しくなるものの、起こる個数を数える方法はすでに習っています。そのため小学算数や中学数学で学ぶ場合の数を理解している場合、和の法則と積の法則は難しくありません。

同じ概念ではあるものの、高校数学では公式や法則を利用することによって問題を解くようになります。そこで、どのように法則を利用すればいいのか理解しましょう。

和の法則と積の法則を理解する

起こる個数を数えるとき、和の法則と積の法則があります。それでは、和の法則や積の法則とは何なのでしょうか。

・和の法則

事象が同時に起こらない場合、和の法則を利用します。例えば、以下の問題の答えは何でしょうか。

• 異なるシャツが4枚、ズボンが3枚あります。一つだけ買える場合、買い方は何通りありますか？

当然ながら、答えは\(4+3=7\)通りです。一つだけ選ぶことになるため、事象が同時に起こることはありません。シャツを2枚買ったり、シャツとズボンの両方を買ったりすることはありません。

買い物によって一つの結果のみ起こるため、事象を足すことによって起こる個数を数えることができます。これが和の法則です。

・積の法則

一方、事象が同時に起こる場合は積の法則を利用します。例えば、以下の答えは何でしょうか。

• 異なるシャツが4枚、ズボンが3枚あります。服を着て外に出かけるとき、シャツとズボンのパターンは何通りですか？

この場合、掛け算をすることによって計算します。樹形図を利用すると、以下のように\(4×3=12\)通りのパターンがあるとわかります。

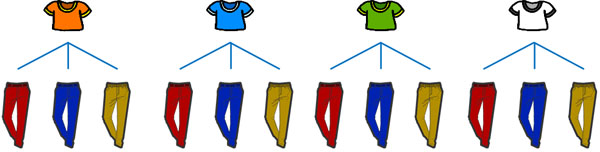
外に出かけるためには、シャツとズボンの両方を着る必要があります。つまり、シャツを選ぶ作業とズボンを選ぶ作業は同時に起こります。

2つの事象が同時に起こるため、掛け算を利用することによって起こる個数を数えます。これを積の法則といいます。

同時に起こらない和の法則：「または」がキーワード

それでは、和の法則と積の法則をどのように見分ければいいのでしょうか。見分け方としては、「または」という言葉がある場合、和の法則を利用しましょう。つまりAまたはBが起こるとき、和の法則が利用されます。

先ほどの例であれば、シャツ（4枚）またはズボン（3枚）の中から、一つだけ買うことができます。つまりシャツを選ぶ事象と、ズボンを選ぶ事象はまったくの別物です。

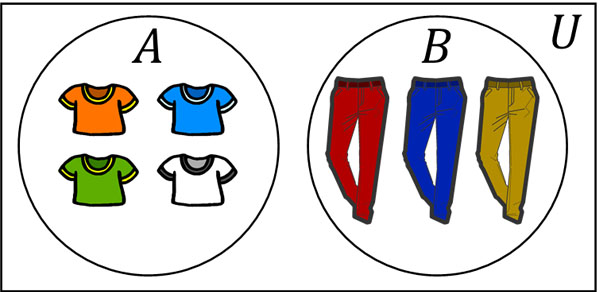
このように関係性のない事象が起こる個数を数えるとき、和の法則を利用します。

場合分けを行い、起こる個数を数える

それでは、実際に和の法則を利用して問題を解いてみましょう。和の法則を利用する場合、場合分けをすることによって問題を解く必要があります。例えば、以下の問題の答えは何でしょうか。

• 2つのサイコロを投げるとき、出る目の和が5の倍数になるケースは何通りか？

2つのサイコロを投げるとき、出る目の和の最高値は12です。また12以下の数で5の倍数になるのは5と10です。つまり、出る目の和が5または10になればいいです。

2つのサイコロを投げ、出る目の和が5になると同時に、出る目の和が10になることはありません。2つの事象が同時に起こることはないのです。結果が5または10になればいいため、和の法則を利用します。

そこで、結果の数を数えてみましょう。出る目の和が5になる事象は4つです。

• (1,4) (2, 3) (3, 2) (4, 1)

また、出る目の和が10になる事象は3つです。

• (4,6) (5, 5) (6, 4)

そこで和の法則を利用し、すべての事象を足しましょう。そうすると、答えは7通りであるとわかります。

同時に起こる積の法則：「かつ」がキーワード

和の法則に対して、積の法則では「かつ」が重要になります。積の法則では事象が同時に起こるため、AかつBのときを考えるのです。

先ほどの例であれば、「シャツを着る、かつズボンを履く」ことになります。シャツとズボンを同時に選ぶことになるため、シャツの個数（4枚）とズボンの個数（3枚）をかけ算しました。

樹形図を描くと、なぜ積の法則で掛け算をすればいいのか理解できます。例えば事象Aが6通りあり、事象Bが3通りある場合、全部の事象は\(6×3=18\)通りになります。

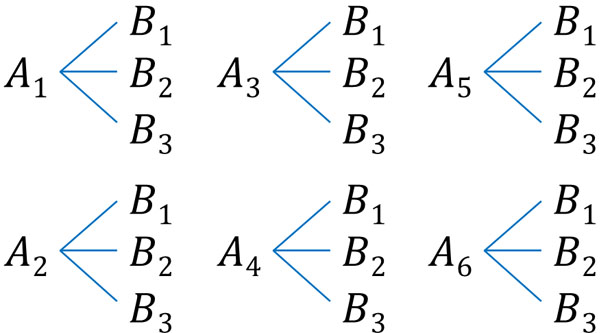
2つが同時に起こるとき、必ず「かつ」を利用することになります。この場合、積の法則を利用しましょう。

正の約数の数を積の法則で理解する

それでは、実際に積の法則を利用して起こる事象を数えてみましょう。例えば、以下の問題はどのように解けばいいでしょうか。

• 200の正の約数は全部で何個でしょうか？

まず、200に対して素因数分解をしましょう。そうすると、200を以下のかけ算に変えることができます。

• 200=2³×5²

つまり、200の正の約数は\(2^a×5^b\)と表現することができます（\(a=\)0, 1, 2, 3: \(b=\)0, 1, 2）。樹形図にすると、約数には以下のパターンがあるとわかります。

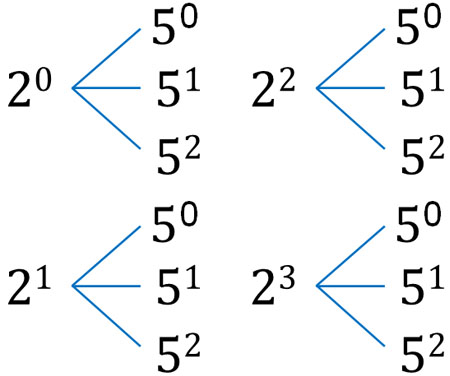
\(2^a\)と\(5^b\)は同時に起こります。そこで、積の法則を利用しましょう。\(a=\)0, 1, 2, 3（4通り）であり、\(b=\)0, 1, 2（3通り）であるため、正の約数は全部で12通りです。

• \(4×3=12\)

なお自然数\(N\)を素因数分解するとき、\(N=P^AQ^BR^C…\)の場合、\(N\)の正の約数の個数は以下の公式によって計算できます。

• \((A+1)(B+1)(C+1)…\)

高校数学の約数でこの公式を習うとき、多くの人はなぜこの公式が成り立つのか理解できません。ただ積の法則を学び、樹形図を利用すれば、なぜこの公式が成り立つのか理解できます。

起こらない事象を考えると素早く解答できる

なお起こる事象を数えるとき、起こらない事象を考えるほうが有効であるケースは多いです。起こる事象を数えるのが大変なとき、起こらない事象を計算しましょう。

例えば、去年の3月に「晴れ」または「くもり」だった日は何日でしょうか。これを計算するとき、雨の日を計算してもいいです。3月は合計で31日あるため、31から雨だった日の合計を引くことによって、「晴れ」または「くもり」の日数を計算できます。

つまり起こらない事象を数えると、起こる事象を計算できるのです。例えば、以下の問題の答えは何でしょうか。

• 3つのサイコロを投げるとき、出る目の積が2の倍数になるケースは何通りか？

出る目の積が2になるとは、つまり積が偶数になることを意味します。ただ、結果が偶数になる個数は多く、数えるのは大変です。そこで、出る目の積が奇数になる個数を数えましょう。

かけ算をするとき、答えが奇数になるためには、すべての数が奇数である必要があります。掛け算をするとき、式の中に偶数があると、答えは必ず偶数になります。サイコロで奇数の数字は1と3と5です。そのため、3つのサイコロを投げて出る目の数が奇数になるケースは27通りです。

• \(3×3×3=27\)

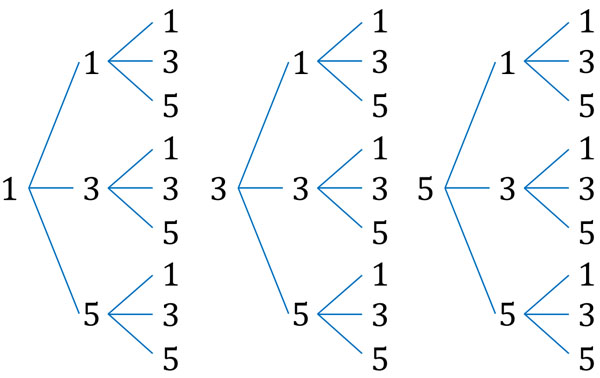
なお3つのサイコロを投げるとき、全事象は\(6×6×6=216\)です。そこで、全事象から答えが奇数になる事象を引きましょう。そうすると、2の倍数（偶数）になる事象を計算できます。

• \(216-27=189\)

こうして、3つのサイコロを投げて出る目の積が2の倍数になるケースは189通りあるとわかります。起こらない事象を考えるというのは、確率の計算をするときについても有効です。そこで、起こらない事象についても考慮するようにしましょう。

和の法則と積の法則を利用して事象を数える

場合の数は小学算数や中学数学で学びます。そのため樹形図を理解している場合、和の法則と積の法則を理解できます。

事象が同時に起こらない場合、和の法則を利用しましょう。事象を数えるとき、「または」が含まれている場合は和の法則を利用します。一方で事象を数えるとき、「かつ」が含まれている場合は積の法則を利用します。

またこれらの事象を数えるとき、起こらない事象についても考慮しましょう。そのほうが素早く計算できるケースがあるからです。

和の法則と積の法則について、どのようなときに利用すればいいのか理解しましょう。なお、たとえ計算方法がわからなくても、樹形図を利用することによって問題を解くことができるはずです。