最も重要な図形の一つが三角形です。三角形が成立するためには条件があります。また三角形には多くの定理があり、その中に辺や角の大小関係があります。
高校数学で学ぶ三角形の成立条件や辺と角の大小関係について、特に新たな内容はありません。当たり前のことを定理として学ぶことになります。
ただ三角形について、辺の大小関係や角の大小関係を用いて証明問題を解かなければいけない場合があります。そのため、三角形の成立条件や辺や角の大小関係を用いた定理が存在することを理解していない場合、証明問題を解くことができません。
それでは、どのように三角形の成立条件を利用し、辺や角の大小関係を用いて証明問題を解けばいいのでしょうか。三角形の成立条件と辺や角の大小関係の内容について、例題を含めて解説していきます。
もくじ
三角形の成立条件では3辺の長さが重要
三角形が存在するかどうかを判定する方法として、三角形の成立条件を利用しましょう。三角形の成立条件では3辺の長さを確認するといいです。
3辺の長さが\(a,b,c\)の場合、三角形が成立するためには、必ず以下の条件を満たさなければいけません。
- \(a<b+c\)
文字にすると、以下のようになります。
- 2辺の長さの和は他の1辺よりも長い
それでは、図を描いて確認してみましょう。3辺の関係について、以下のようになります。
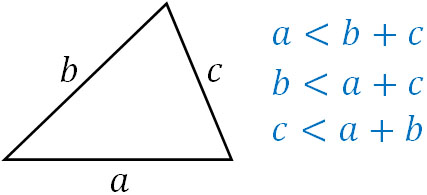
当然ではありますが、\(a≧b+c\)のケースでは三角形を作ることができません。以下のような図になってしまうからです。
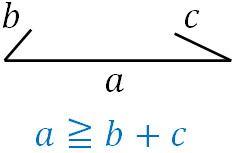
三角形が成立するためには、2辺の長さの和が他の辺の長さよりも大きくなる必要があるのです。
なお先ほどの図について、引き算を利用して三角形の成立条件を表すこともできます。3辺の長さが\(a,b,c\)の場合、以下のようになります。
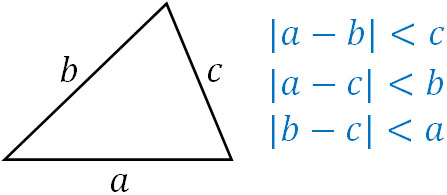
文章にすると以下のようになります。
- 2辺の長さの差(絶対値)は他の1辺よりも短い
一方で\(|a-b|≧c\)の場合、三角形を作れません。
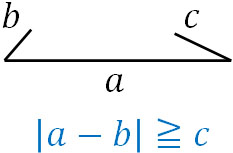
このように和または差を利用することによって、三角形の成立条件を確認できます。
辺の取りうる長さの範囲を求める
それでは、三角形の成立条件を用いて問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 3辺の長さが3、\(x\)、\(9-x\)の三角形があります。\(x\)の取りうる範囲を求めましょう。
三角形の成立条件を利用して、この問題を解きましょう。まず、以下の図を作ります。
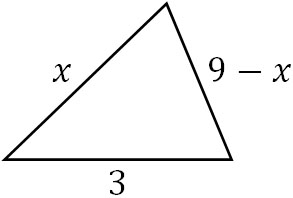
正確な辺の長さはわかりません。ただ三角形の成立条件を満たすためには、「\(x\)と\(9-x\)の和が3よりも大きい、または\(x\)と\(9-x\)の差の絶対値が3よりも小さければいい」とわかります。そのため、以下の関係になります。
\(|x-(9-x)|<3<x+(9-x)\)
\(|2x-9|<3<9\)
そこで、\(|2x-9|<3\)を解きましょう。
\(|2x-9|<3\)
\(-3<2x-9<3\)
\(6<2x<12\)
\(3<x<6\)
こうして、三角形が成立する条件は\(x\)の範囲が\(3<x<6\)であるとわかります。
三角形の辺と角の大小関係
三角形の成立条件では辺を利用しました。次に辺と角の大小関係を学びましょう。三角形の辺と角には、以下の関係があります。
- 辺が長い場合、対角は大きい(辺が短い場合、対角は小さい)
例えば、△ABCについて以下のようになります。

辺が長い場合、対角は大きいです。当たり前のことを述べているにすぎませんが、高校数学ではこの性質を利用して証明問題を解かなければいけない場合があります。そのため、三角形で辺と角の大小関係を把握することは重要です。
定理の逆が成り立つ:角度が大きい場合、対辺は長い
なお、先ほどの定理は逆も成り立ちます。角度が大きい場合、対辺の長さは大きくなるのです。これは、以下のように図を描けば容易に理解できます。
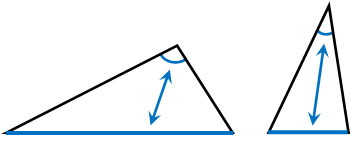
辺の長さと角度の大きさは比例します。辺が長い場合、対角は大きくなります。一方で辺が短い場合、対角は小さくなります。また、その逆も成り立ちます。
二等辺三角形では、二辺が等しく、さらには2つの角度が等しいことを既に習っていると思います。この理由として、辺の長さと角度の大きさは比例するからです。
辺と角度を利用し、証明問題を解く
それでは、三角形の辺と角の大小関係を利用して証明問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 直角三角形では斜辺が最も長い辺であることを証明しましょう。
三平方の定理を利用することからわかる通り、直角三角形では斜辺が最も長いのは感覚的にわかります。ただ、証明するとなると多くの人が困ります。そこで辺と角の大小関係を利用しましょう。そうすれば、容易に問題を解くことができます。
直角三角形ABCについて、∠A=90°とします。この場合、∠B+∠C=90°なので、∠Aは∠Bや∠Cよりも角度が大きいです。∠Aが最も大きい角であるため、対辺である斜辺の長さは最も大きいです。
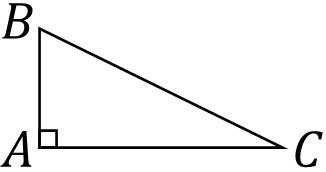
こうして、直角三角形の斜辺が最も長いと証明できました。辺の長さや角度の大きさを比較する証明問題については、辺と角の大小関係を利用しましょう。
三角形の成立条件と辺と角の大小関係を利用する
証明問題で利用されるのが三角形の成立条件と辺と角の大小関係です。三角形には多くの定理があります。その中でも、辺と角度を利用する定理が存在します。
三角形の成立条件については、新たな内容ではありません。ただ三角形の成立条件を理解していないと、計算問題や証明問題を解けません。
同じことは三角形の辺と角の大小関係にもいえます。辺が長い場合、対角が大きくなるのは当然です。ただこの定理が存在することを理解していないと、証明問題を解くことができません。そのため、こうした定理があることを知っておくことが重要です。
高校数学で学ぶ内容が三角形の成立条件と辺と角の大小関係です。これらの定理を利用して、証明問題を解けるようになりましょう。






