二次曲線による軌跡を考えるとき、離心率と準線の概念を学ぶことは重要です。放物線や楕円、双曲線を定義するとき、焦点を利用します。このとき楕円と双曲線は2つの焦点を利用して定義するため、放物線とは概念が異なるように思えてしまいます。
ただ放物線だけでなく、楕円と双曲線についても一つの焦点を利用して描くことができます。そのため放物線、楕円、双曲線はすべて関係しています。
離心率と準線を利用することにより、二次曲線は放物線、楕円、双曲線になることができます。そこで、どのように離心率を利用して楕円と双曲線を描けばいいのか解説していきます。
もくじ
二次曲線の離心率と準線
まず、離心率とは何かを学びましょう。放物線では、焦点Fと準線からの距離が等しくなります。下図について、\(AH=AF\)となるのです。

それでは\(AH:AF=1:1\)ではなく、\(AH:AF=1:e\)とします。このとき、準線と点Aとの距離AHを1とするとき、点Aから焦点Fまでの距離AFを\(e\)とすると、\(e\)を離心率といいます。

\(e=1\)のとき、二次曲線は放物線になります。
離心率\(e\)の値:放物線、楕円、双曲線の変化
それでは、離心率\(e\)の値が変化することによって二次曲線の形はどのように変わるのでしょうか。\(e\)の値により、二次曲線は以下のように変化します。
- \(0<e<1\):楕円
- \(e=1\):放物線
- \(e>1\):双曲線
それでは、以下の問題を解いてみましょう。
- 点F\((2,0)\)からの距離と直線\(x=\displaystyle\frac{1}{2}\)からの距離が\(2:1\)となる点Pの軌道を求めましょう。
点Pの座標を\((x,y)\)とします。また、点Pから直線\(x=\displaystyle\frac{1}{2}\)に向けて垂線を引くとき、交点をHとします。この場合、以下の図を描くことができます。
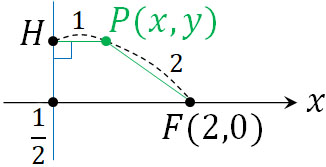
点Pと点Hとの距離は\(|x-\displaystyle\frac{1}{2}|\)です。また、点Pと点Fとの距離は\(\sqrt{(x-2)^2+y^2}\)です。そこで、以下のように計算しましょう。
\(PH:PF=1:2\)
\(2PH=PF\)
\(4PH^2=PF^2\)
\(4|x-\displaystyle\frac{1}{2}|^2=(x-2)^2+y^2\)
\(4(x-\displaystyle\frac{1}{2})^2=(x-2)^2+y^2\)
\(4x^2-4x+1\)\(=x^2-4x+4+y^2\)
\(3x^2-y^2=3\)
\(x^2-\displaystyle\frac{y^2}{3}=1\)
こうして、双曲線の方程式を得ることができました。\(e>1\)であるため、双曲線の方程式を得られるのです。
離心率と二次曲線の関係性の証明
それでは、離心率と二次曲線の関係性を証明しましょう。点F\((c,0)\)(\(c>0\))と点P\((x,y)\)があり、点Pから\(y\)軸(\(x=0\))に対して垂線をおろすときの交点をHとします。また、\(PH:PF=1:e\)です。
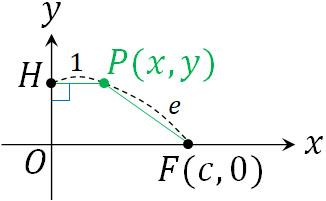
HPの長さは\(|x|\)です。また、PFの長さは\(\sqrt{(x-c)^2+y^2}\)です。そこで、先ほどと同じように、以下のように計算しましょう。
\(PH:PF=1:e\)
\(ePH=PF\)
\(e^2PH^2=PF^2\)
\(e^2x^2=(x-c)^2+y^2\)
\(e^2x^2=x^2-2xc+c^2+y^2\)
\((1-e^2)x^2-2xc+y^2=-c^2\)
この式に対して平方完成をします。
\((1-e^2)\left(x-\displaystyle\frac{c}{1-e^2}\right)^2+y^2\)\(=-c^2+\displaystyle\frac{c^2}{1-e^2}\)
\((1-e^2)\left(x-\displaystyle\frac{c}{1-e^2}\right)^2+y^2\)\(=\displaystyle\frac{c^2e^2}{1-e^2}\)
なお、この状態では式が少し複雑なので、\(x\)軸方向に\(-\displaystyle\frac{c}{1-e^2}\)だけ移動させましょう。そうすると、式は以下のようになります。
\((1-e^2)x^2+y^2\)\(=\displaystyle\frac{c^2e^2}{1-e^2}\)
この式を利用することにより、二次曲線を計算できます。
離心率を利用して楕円と双曲線の方程式を計算する
それでは、場合分けをすることによって楕円と双曲線の方程式を計算しましょう。
・\(0<e<1\)のとき
\(a=\displaystyle\frac{ce}{1-e^2}\)、\(b=\displaystyle\frac{ce}{\sqrt{1-e^2}}\)とすると、以下のように計算できます。
\((1-e^2)x^2+y^2\)\(=\displaystyle\frac{c^2e^2}{1-e^2}\)
\(\displaystyle\frac{cex^2}{a}+y^2\)\(=b^2\)
\(\displaystyle\frac{b^2x^2}{a^2}+y^2\)\(=b^2\)
\(\displaystyle\frac{x^2}{a^2}+\displaystyle\frac{y^2}{b^2}\)\(=1\)
こうして、楕円の方程式を作ることができました。離心率が\(0<e<1\)の場合、二次曲線は楕円となるのです。
・\(e>1\)のとき
一方で\(e>1\)の場合、\((1-e^2)\)の値はマイナスになります。そこで、以下の式について両辺に\(-1\)をかけることで、\(x^2\)の係数が正の値になるように変形しましょう。
\((1-e^2)x^2+y^2\)\(=\displaystyle\frac{c^2e^2}{1-e^2}\)
\((e^2-1)x^2-y^2\)\(=\displaystyle\frac{c^2e^2}{e^2-1}\)
\(a=\displaystyle\frac{ce}{e^2-1}\)、\(b=\displaystyle\frac{ce}{\sqrt{e^2-1}}\)とすると、以下のように計算できます。
\((e^2-1)x^2-y^2\)\(=\displaystyle\frac{c^2e^2}{e^2-1}\)
\(\displaystyle\frac{cex^2}{a}-y^2\)\(=b^2\)
\(\displaystyle\frac{b^2x^2}{a^2}-y^2\)\(=b^2\)
\(\displaystyle\frac{x^2}{a^2}-\displaystyle\frac{y^2}{b^2}\)\(=1\)
こうして、双曲線の方程式を作ることができました。
離心率を利用して計算する
準線を利用して図を作れる二次曲線は放物線だけではありません。楕円と双曲線についても、準線を利用することで図を描くことができます。
放物線の場合、離心率\(e\)の値は1です。一方、離心率が\(0<e<1\)の場合、二次曲線は楕円になります。また、離心率が\(e>1\)の場合、二次曲線は双曲線になります。準線と焦点からの距離の割合によって、図形は放物線、楕円、双曲線と変化するのです。
なお離心率を用いて図形の計算をするとき、辺の比や点と点の長さを計算することにより、軌道の方程式を得ましょう。これにより、二次曲線の方程式を計算できます。
離心率を学べば、放物線や楕円、双曲線が関連しているとわかります。離心率がどのような概念なのか学び、離心率と準線を用いて軌道を計算できるようになりましょう。






