日常生活で指数を含む計算式を利用することは多いです。例えば投資での金利計算では指数を利用します。人口の計算でも指数がひんぱんに利用されます。ニュースで利用される統計データで指数が利用されることは多いのです。
それでは、指数の計算をするためにはどうすればいいのでしょうか。指数の計算では、指数法則を学ぶ必要があります。また、累乗根の性質を理解しなければいけません。
それに加えて、指数関数の計算方法を学びましょう。指数を含む方程式を解くことにより、答えを得られるようにするのです。このときは置き換えを利用して計算することも多いです。
日々の生活で指数が利用されることは多いため、高校数学で必ず理解しなければいけない内容の一つです。そこで指数法則や累乗根の性質、指数関数の計算方法を解説していきます。
もくじ
指数法則を用いて計算する
計算するためにはルールを知らなければいけません。そのため指数法則を学ぶ必要があります。\(a^0=1\)になるのは既に知っていると思います。それ以外に指数法則については、以下のようになります
- \(a^ma^n=a^{m+n}\)
- \((a^m)^n=a^{mn}\)
- \((ab)^n=a^nb^n\)
※\(a≠0\)、\(b≠0\)であり、\(m\)と\(n\)は整数。
これらの関係は容易に理解できると思います。具体的な数字に置き換えると以下のようになります。
- \(2^22^3=2^{2+3}\)
- \((2^2)^3=2^{2×3}\)
- \((2×3)^4=2^43^4\)
なお、\(a^{-n}\)は\(\displaystyle\frac{1}{a^n}\)を意味しています。\(a^{-n}=\displaystyle\frac{1}{a^n}\)であるため、以下の関係が成り立ちます。
- \(\displaystyle\frac{a^m}{a^n}=a^{m-n}\)
- \(\left(\displaystyle\frac{a}{b}\right)^n=\displaystyle\frac{a^n}{b^n}=a^n×b^{-n}\)
※\(a≠0\)、\(b≠0\)であり、\(m\)と\(n\)は整数。
累乗根の性質と指数での表記
なお指数を学ぶとき、同時に累乗根の性質を理解しましょう。\(\sqrt{a}\)の性質は既に理解していると思います。\(\sqrt{a}\)を二乗すると、答えは\(a\)になります。
それでは、\(\sqrt[3]{a}\)は何を意味しているでしょうか。\(\sqrt[3]{a}\)とは、\(\sqrt[3]{a}\)を3乗すると答えが\(a\)になることを表しています。つまり、\((\sqrt[n]{a})^n=a\)です。そのため、累乗根を指数で表すと以下のようになります。
- \(\sqrt[n]{a}=a^{\frac{1}{n}}\)
例えば、\((\sqrt[3]{a})^3=a\)です。また、\(a^{\frac{1}{3}}\)\(×a^{\frac{1}{3}}\)\(×a^{\frac{1}{3}}\)\(=a\)です。そのため、\(\sqrt[3]{a}=a^{\frac{1}{3}}\)であることがわかります。なお\(a>0\)、\(b>0\)であり、\(m\)、\(n\)、\(p\)が正の整数であるとき、以下が累乗根の性質です。
- \(\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}\)
- \(\displaystyle\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\displaystyle\frac{a}{b}}\)
- \((\sqrt[n]{a})^m=\sqrt[n]{a^m}\)
- \(\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}\)
- \(\sqrt[n]{a^m}=\sqrt[np]{a^{mp}}\)
先ほどの説明を理解すれば、これらの性質は問題なく理解できると思います。例えば\(\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}\)であれば、以下のようになります。
\(\sqrt[n]{a}\sqrt[n]{b}\)
\(=a^{\frac{1}{n}}b^{\frac{1}{n}}\)
\(=(ab)^{\frac{1}{n}}\)
\(=\sqrt[n]{ab}\)
2乗根同士や3乗根同士など、\(n\)乗根が同じ場合はかけ算をすることができます。いずれにしても、指数法則と同時に累乗根の性質も理解しましょう。それでは、以下の値は何でしょうか。
- \(\sqrt[6]{3^3}\)
指数と累乗根の性質を利用して計算しましょう。
\(\sqrt[6]{3^3}\)
\(=3^{\frac{3}{6}}\)
\(=3^{\frac{1}{2}}\)
\(=\sqrt{3}\)
こうして、式を計算することができました。なお実際のところ、累乗根を指数で表せば累乗根の性質を覚えなくても計算できるようになります。例題として、以下の問題を解いてみましょう。
- \(\sqrt[3]{5}×25×\sqrt[3]{25}\)
計算すると以下のようになります。
\(\sqrt[3]{5}×25×\sqrt[3]{25}\)
\(=5^{\frac{1}{3}}×5^2×5^{\frac{2}{3}}\)
\(=5^{\frac{1}{3}+2+\frac{2}{3}}\)
\(=5^3\)
\(=125\)
累乗根を含む計算では、指数法則を覚えることが重要です。新しい概念ではないものの、指数や累乗根を含む式を計算できるようになりましょう。
指数を含む式のかけ算や割り算
ここまでの知識を利用して、指数や累乗根を含む式の応用問題を解けるようになりましょう。以下の問題の答えは何でしょうか。
- \(a>0\)であり、\(a^{\frac{1}{3}}+a^{-\frac{1}{3}}=\sqrt{7}\)のとき、\(a+a^{-1}\)の値は何でしょうか。
公式を利用して\(a+a^{-1}\)を変形しましょう。問題文より、\(a^{\frac{1}{3}}+a^{-\frac{1}{3}}\)を利用する必要があります。そこで\(a=(a^{\frac{1}{3}})^3\)、\(a^{-1}=(a^{-\frac{1}{3}})^3\)と考えましょう。そこで、展開公式を利用して以下のように計算します。
\(a+a^{-1}\)
\(=(a^{\frac{1}{3}})^3+(a^{-\frac{1}{3}})^3\)
\(=(a^{\frac{1}{3}}+a^{-\frac{1}{3}})^3\)\(-3a^{\frac{1}{3}}a^{-\frac{1}{3}}\)\((a^{\frac{1}{3}}+a^{-\frac{1}{3}})\)
\(=(\sqrt{7})^3-3×1×\sqrt{7}\)
\(=4\sqrt{7}\)
展開の公式より、\((a+b)^3\)\(=a^3+3a^2b+3ab^2+b^3\)です。つまり、\((a+b)^3\)\(=a^3+b^3+3ab(a+b)\)です。この公式を利用することによって、\(a+a^{-1}=4\sqrt{7}\)とわかりました。
指数関数の性質とグラフの形
指数や累乗根の計算は難しくないため、必ず行えるようになりましょう。重要なのは指数の計算をすることではなく、指数関数を学ぶことにあります。\(y=a^x\)が指数関数です。このとき、\(a>1\)と\(0<a<1\)では指数関数のグラフの形が異なります。それぞれのグラフは以下のようになります。
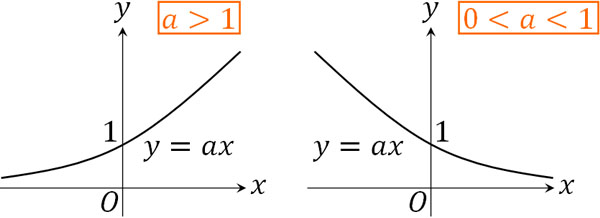
例えば\(y=2^x\)の場合、\(x\)の値が大きくなると\(y\)の値も大きくなります。一方で\(y=\left(\displaystyle\frac{1}{2}\right)^x\)の場合、\(x\)の値が大きくなると\(y\)の値は小さくなります。そのため、グラフは上図のようになります。
それでは、\(y=4-16^{\frac{x}{2}}\)のグラフを描いてみましょう。式を計算すると以下のように変形できます。
\(y=4-16^{\frac{x}{2}}\)
\(y=4-(4^2)^{\frac{x}{2}}\)
\(y=-4^x+4\)
\(y=4^x\)のグラフに対して、\(x\)軸を基準に対称移動し、\(y\)軸方向に4移動すると\(y=-4^x+4\)になります。そのため、グラフは以下のようになります。
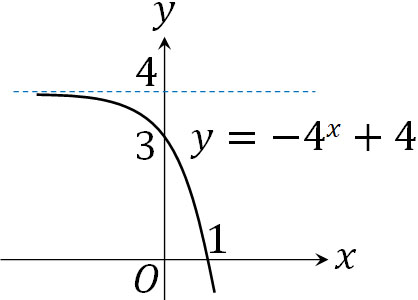
指数関数を理解するためには、グラフを描けるようになる必要があります。そこで、どのようなグラフを作ればいいのか学びましょう。
指数方程式を解く:置き換えの利用
それでは、指数方程式を解いてみましょう。式に指数を含む場合、計算が複雑になります。そこでほかの文字に置き換えることによって計算する方法が一般的です。それでは、以下の指数方程式の答えは何でしょうか。
- \(2^{2x}-12·2^x+32=0\)
このままでは計算が難しいです。そこで、\(2^x=t\)と考えて置き換えをしましょう。これにより、以下のように計算できます。
\(t^2-12t+32=0\)
\((t-4)(t-8)=0\)
\(t=4,8\)
つまり\(2^x=4,8\)です。そのため、\(x=2,3\)とわかります。次に、以下の連立方程式を解いてみましょう。
\(\begin{eqnarray} \left\{\begin{array}{l}2^x-7·3^y=1\\2^x+2·3^y=10\end{array}\right.\end{eqnarray}\)
計算しやすくするため、\(2^x=X\)、\(3^y=Y\)としましょう。そうすると、式は以下のようになります。
\(\begin{eqnarray} \left\{\begin{array}{l}X-7Y=1\\X+2Y=10\end{array}\right.\end{eqnarray}\)
連立方程式を解くと、以下のようになります。
\(-9Y=-9\)
\(Y=1\)
なお\(Y=1\)であるため、\(X=8\)です。そのため\(x=3\)、\(y=0\)とわかります。
指数不等式の解き方
次に指数不等式を解けるようになりましょう。指数方程式を解くとき、置き換えをする前に底をそろえる必要があります。指数不等式も同様であり、底をそろえた後に大小関係を比較しましょう。
なお\(y=a^x\)について、底\(a\)が1よりも値が大きいのか、それとも小さいのかによって大小関係が変化します。以下のようになります。
- \(a>1\)の場合:\(p<q\)なら、\(a^p<a^q\)
- \(0<a<1\)の場合:\(p<q\)なら、\(a^p>a^q\)
それでは、指数不等式に関する次の問題を解いてみましょう。
- \(\left(\displaystyle\frac{1}{3}\right)^{x-4}<\displaystyle\frac{1}{9}\)
以下のように計算しましょう。
\(\left(\displaystyle\frac{1}{3}\right)^{x-4}<\displaystyle\frac{1}{9}\)
\(\left(\displaystyle\frac{1}{3}\right)^{x-4}<\left(\displaystyle\frac{1}{3}\right)^2\)
底は1より小さいため、不等号は以下のようになります。
\(x-4>2\)
\(x>6\)
こうして、指数不等式の答えを得ることができました。難しい内容ではないものの、底\(a\)の値によって不等式の向きが変化することに注意しましょう。
指数関数の最大値と最小値
ここまでの内容を理解したうえで、指数関数を解けるようになりましょう。置き換えを利用すれば、指数関数は二次関数や三次関数と同じ内容になります。なお置き換えをするとき、値の取り得る範囲に注意して計算しましょう。
それでは、指数関数に関する以下の問題の答えは何でしょうか。
- \(y=2(4^x+4^{-x})-5(2^x+2^{-x})+8\)について、\(t=2^x+2^{-x}\)とするとき、最小値と最大値を求めましょう。なお、\(x≦2\)です。
まず、\(t^2\)を計算しましょう。以下のようになります。
\(t^2=(2^x)^2+2·2^x·2^{-x}+(2^{-x})^2\)
\(t^2=4^x+2+4^{-x}\)
\(4^x+4^{-x}=t^2-2\)
そこで、置き換えをすることで計算しましょう。
\(y=2(4^x+4^{-x})-5(2^x+2^{-x})+8\)
\(y=2(t^2-2)-5t+8\)
\(y=2t^2-5t+4\)
\(y=2\left(t^2-\displaystyle\frac{5}{2}t\right)+4\)
\(y=2\left(t-\displaystyle\frac{5}{4}\right)^2+\displaystyle\frac{7}{8}\)
それでは、\(t=\displaystyle\frac{5}{4}\)のとき最小値なのでしょうか。実は、最小値が\(t=\displaystyle\frac{5}{4}\)だと不正解です。\(t=\displaystyle\frac{5}{4}\)となる\(x\)の値は存在しないからです。
そこで、\(t\)の最小値を求めましょう。相加平均・相乗平均の関係より、以下のように計算しましょう。
\(2^x+2^{-x}≧2\sqrt{2^x·2^{-x}}\)
\(2^x+2^{-x}≧2\)
\(t≧2\)
こうして、最小値は\(t=2\)のときとわかります。\(t=2\)を代入すると\(y=2\)となります。また\(t=2\)となるのは\(2^x=2^{-x}\)のときです。つまり\(x=0\)のとき、最小値2となります。
なお問題文より、\(x≦2\)です。\(x=2\)のとき、 \(t=2^2+2^{-2}=\displaystyle\frac{9}{4}\)です。そこで、\(t=\displaystyle\frac{9}{4}\)を代入しましょう。
\(y=2\left(\displaystyle\frac{9}{4}\right)^2-5\left(\displaystyle\frac{9}{4}\right)+4\)
\(y=\displaystyle\frac{23}{8}\)
こうして\(t=\displaystyle\frac{9}{4}\)、つまり\(x=2\)のとき、最大値\(\displaystyle\frac{23}{8}\)とわかりました。
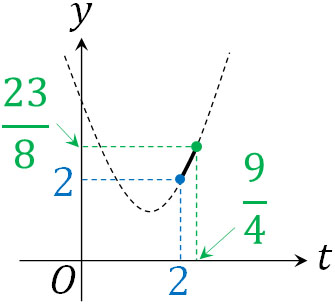
指数関数では、置き換えによって計算するケースが多いです。ただ二次関数や三次関数で得た図形を見て、答えを出してはいけません。置き換えした文字はすべての値を取れるわけではなく、範囲があります。そこで、どの範囲で動くことができるのか確認しましょう。
指数と累乗根の性質を学び、指数関数を計算する
日常生活の多くの場面で指数の計算が行われています。統計データで指数が利用されているのは普通であるため、指数を理解していないと金融や経済などのニュース内容がわかりません。そのため、指数は必須の知識といえます。
なお指数と密接に関わる内容が累乗根です。累乗根の性質を覚える必要はなく、累乗根を指数に変換すれば容易に計算できます。そこで、指数法則を覚えることで指数を計算できるようになりましょう。
指数法則を利用できるようになれば、指数方程式や指数不等式を計算できます。また、指数関数を解けるようにもなりましょう。置き換えを利用したり、範囲の確認をしたりすることで答えを得るのです。
指数に特有の性質が存在します。そこで指数法則を覚え、指数の計算方法を学び、指数関数の答えを得られるようになりましょう。






