平面で作ることのできる図形に円があります。このとき、円を空間図形で表すと球になります。そこで、球面の方程式を利用できるようになりましょう。
球面の方程式には、標準形と一般形の2つの表し方があります。どちらの方法を利用してもいいですが、式を確認することで中心座標や半径がわかるようになる必要があります。
なお空間座標を利用する場合、ベクトルを利用して計算することも多いです。そこで、球面のベクトル方程式を用いて、球面の方程式を計算できるようになりましょう。公式は円のベクトル方程式と同じであるため、公式を新たに覚える必要はありません。
それでは、どのように球面の方程式を利用すればいいのでしょうか。公式や半径の求め方、球面のベクトル方程式について解説していきます。
もくじ
空間座標での球面の方程式:標準形の公式
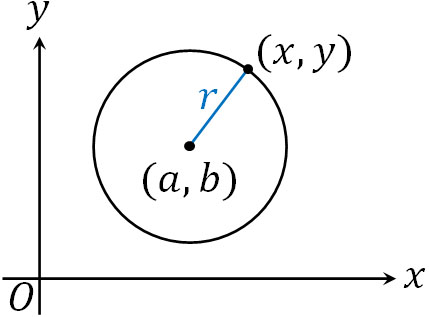
球面の方程式を学ぶ前に、円の方程式を復習しましょう。円の中心を\((a,b)\)、半径を\(r\)とするとき、円の方程式を以下のように表すことができます。
- \((x-a)^2+(y-b)^2=r^2\)
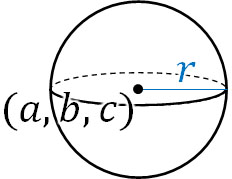
このとき、球面の方程式と円の方程式は似ています。球では立体図形になるため、\(z\)座標を加える必要があります。そこで球の中心を\((a,b,c)\)、半径を\(r\)とすると、以下のように球面の方程式を表すことができます。
- \((x-a)^2+(y-b)^2+(z-c)^2=r^2\)
 例えば球の中心が\((2,1,3)\)、半径が\(3\)の場合、球面の方程式は以下になります。
例えば球の中心が\((2,1,3)\)、半径が\(3\)の場合、球面の方程式は以下になります。
- \((x-2)^2+(y-1)^2+(z-3)^2=9\)
それでは、以下の問題を解いてみましょう。
- 点A\((2,1,1)\)を通り、3つの座標平面に接する球面の方程式を求めましょう。
3つの座標平面(\(x\)軸、\(y\)軸、\(z\)軸)に接するため、球の中心座標は\((r,r,r)\)です。
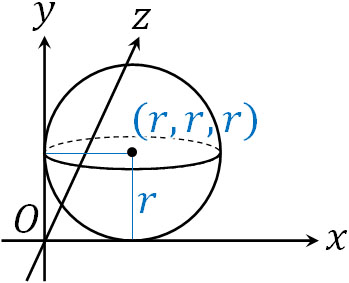
そのため、以下の式を作ることができます。
- \((x-r)^2+(y-r)^2+(z-r)^2=r^2\)
この球は点A\((2,1,1)\)を通るため、以下のように代入して計算しましょう。
\((2-r)^2+(1-r)^2+(1-r)^2=r^2\)
\(3r^2-8r+6=r^2\)
\(2r^2-8r+6=0\)
\(r^2-4r+3=0\)
\((r-1)(r-3)=0\)
こうして、\(r=1,3\)とわかりました。つまり、以下の2つが答えです。
- \((x-1)^2+(y-1)^2+(z-1)^2=1\)
- \((x-3)^2+(y-3)^2+(z-3)^2=9\)
球面の方程式を利用することにより、答えを得られるようになりましょう。
球面の方程式を一般形で表す
なお場合によっては、一般形を利用して球面の方程式を表すこともあります。円の方程式を一般形で表すと以下のようになります。
- \(x^2+y^2+ax+by+c=0\)
そこで、球面の方程式では\(z\)軸を考慮しましょう。以下が球面の方程式の一般形です。
- \(x^2+y^2+z^2+ax+by+cz+d=0\)
円の方程式を覚えていれば、球面の方程式を覚えるのは簡単です。なお4点がわかれば、公式を利用することにより、一般形での球面の方程式を得ることができます。
軸に垂直な平面と球面が交わってできる円の方程式
なお球面の方程式を学ぶとき、応用問題を解けるようになりましょう。球面と平面の交点によって作られる円の方程式を求めるのは応用問題の一つです。
まず、軸に対して垂直な平面と球面の交点を考えましょう。軸に対して垂直な平面では、\(x\)軸、\(y\)軸、\(z\)軸のうち、必ずどれかの値が固定されます。例えば\(y=2\)の場合は以下のようになります。
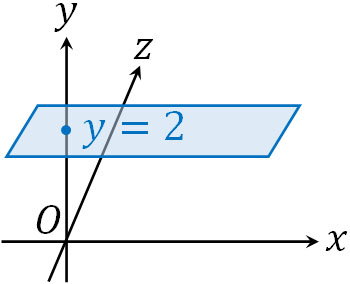
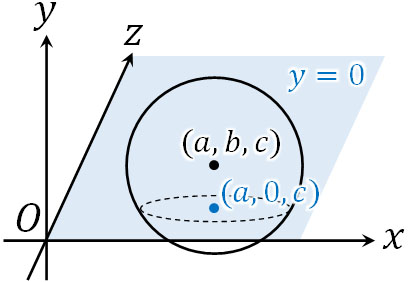
特に、軸上に平面が存在する場合は値がゼロになります。例えば\(y=0\)の場合、\(xz\)平面と呼ばれます。\(y=0\)であるため、\(x\)軸と\(z\)軸を含む平面を表すことができるのです。
例えば球が\(xz\)平面と交わるとき、どのような円が作られるでしょうか。\(xz\)平面では前述の通り\(y=0\)となるため、球面の公式に\(y=0\)を代入しましょう。そのため、球と\(xz\)平面の交点によって作られる円の方程式は以下のようになります。
\((x-a)^2+(0-b)^2+(z-c)^2=r^2\)
\((x-a)^2+(z-c)^2=r^2-b^2\)
それでは、以下の問題を解いてみましょう。
- 中心が\((-1,2,3)\)であり、半径が6の球について、\(xy\)平面との交点によって作られる円の方程式を求めましょう。
球面の方程式は以下になります。
- \((x+1)^2+(y-2)^2+(z-3)^2=36\)
\(xy\)平面と交わるというのは、\(z=0\)であることを意味します。そこで、\(z=0\)を代入しましょう。
\((x+1)^2+(y-2)^2+(0-3)^2=36\)
\((x+1)^2+(y-2)^2=27\)
こうして、球と\(xy\)平面の交点によって作られる円の方程式を得ることができました。
球面のベクトル方程式と公式
球面を学ぶとき、球面の方程式だけでなく、球面のベクトル方程式を利用できるようになりましょう。座標を用いて球面の方程式を表すだけでなく、位置ベクトルを利用することによって球の性質を表すことができます。
球面のベクトル方程式は円のベクトル方程式と公式が同じです。要は、同じ概念であると考えましょう。
中心がC(\(\overrightarrow{c}\))、半径(中心と球面の距離)が\(r\)、球面上の点をP(\(\overrightarrow{p}\))とします。\(\overrightarrow{CP}\)は中心Cから点Pまでのベクトルを表します。また、点Cから点Pまでの距離は\(r\)であるため、以下の式を作れます。
- \(|\overrightarrow{CP}|=r\)
なお\(\overrightarrow{CP}=\overrightarrow{OP}-\overrightarrow{OC}\)\(=\overrightarrow{p}-\overrightarrow{c}\)であるため、以下のように式を変形しましょう。
- \(|\overrightarrow{p}-\overrightarrow{c}|=r\)

こうして、球面のベクトル方程式を導出できました。また公式を確認すると、前述の通り円のベクトル方程式と同じであるとわかります。
また、両辺を二乗しましょう。そうすると、式は以下のようになります。
\(|\overrightarrow{p}-\overrightarrow{c}|^2=r^2\)
\((\overrightarrow{p}-\overrightarrow{c})^2=r^2\)
こうして、もう一つのベクトル方程式である\((\overrightarrow{p}-\overrightarrow{c})^2=r^2\)を作れます。
・中心を通る直径の両端がわかっているケース
円のベクトル方程式を学んでいる場合、もう一つベクトル方程式が存在することを知っていると思います。球についても概念が同じであるため、当然ながら球面のベクトル方程式にも、ほかに公式があります。
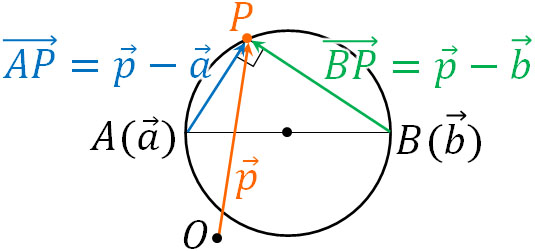
球の中心を通る直径について、両端の点をそれぞれA(\(\overrightarrow{a}\))、B(\(\overrightarrow{b}\))とします。また、球上にある任意の点をP(\(\overrightarrow{p}\))とします。
この場合、直径は中心を通るので線分APと線分BPは必ず垂直になります。つまり\(\overrightarrow{AP}·\overrightarrow{BP}=0\)となり、以下の関係が成り立ちます。
- \((\overrightarrow{p}-\overrightarrow{a})·(\overrightarrow{p}-\overrightarrow{b})=0\)
こうして、球面のベクトル方程式を得ることができました。このベクトル方程式についても、円のベクトル方程式と球面のベクトル方程式で式が同じです。
直径の両端を用いて方程式を得る
それでは、ベクトル方程式を利用して計算問題を解いてみましょう。以下の問題の答えは何でしょうか。
- 点A\((1,2,4)\)と点B\((-5,8,-2)\)を直径の両端とする球について、ベクトル方程式を用いて球面の方程式を計算しましょう。
球面のベクトル方程式を利用しなくても、球面の方程式を得ることは可能です。ただ、ここでは球面のベクトル方程式を用いて計算しましょう。球上の点をP(\(\overrightarrow{P}\))とします。\(\overrightarrow{P}=(x,y,z)\)の場合、以下のようになります。
- \(\overrightarrow{AP}=(x-1,y-2,z-4)\)
- \(\overrightarrow{BP}=(x+5,y-8,z+2)\)
そこで、以下のように計算しましょう。
\(\overrightarrow{AP}·\overrightarrow{BP}=0\)
\((x-1)(x+5)+(y-2)(y-8)\)\(+(z-4)(z+2)\)\(=0\)
\(x^2+y^2+z^2+4x-10y-2z+3\)\(=0\)
こうして、球面のベクトル方程式を利用して球面の方程式を得ることができました。
球面の方程式とベクトルを利用する
立体図形では、平面図形に対して\(z\)軸が加わります。そのため、計算で利用する公式は少し複雑になります。ただ円の方程式と球面の方程式を比べると、式の形はほぼ同じです。そのため、新たに公式を覚える必要はありません。
そこで標準形と一般形の両方にて、球面の方程式を利用できるようになりましょう。このとき、軸に垂直な平面と球面の交点によって作られる円の計算を行えるようになる必要があります。
また球の計算問題では、ベクトル方程式を活用することも重要です。円のベクトル方程式と球面のベクトル方程式は公式が同じです。そのためベクトル方程式を利用するときについても、新たに覚える内容はありません。
円の方程式を少し複雑にした内容が球面の方程式です。そこで公式の利用法を学び、球の方程式を得られるようになりましょう。






