空間ベクトルでの位置ベクトルと図形：公式や平面との交点座標

ベクトルで重要な概念に位置ベクトルがあります。原点Oを始点とするベクトルが位置ベクトルであり、空間ベクトルでひんぱんに利用されます。

平面ベクトルでも空間ベクトルでも、位置ベクトルの概念は同じです。そのため利用する公式は同じであり、平面ベクトルを理解している場合、空間ベクトルでの位置ベクトルを理解するのは難しくありません。

なお空間ベクトルに特有の条件に共面条件があります。ただこの条件についても、平面ベクトルで位置ベクトルを学んでいる場合は容易に理解できます。

それでは空間ベクトルでどのように位置ベクトルを利用し、計算問題を解けばいいのでしょうか。位置ベクトルを利用するときの公式や問題の解き方を解説していきます。

1 空間ベクトルでの内分点、外分点、重心の公式
- 1.1 共線条件・共点条件は平面ベクトルと空間ベクトルで同じ
- 1.2 共面条件では、係数を足すと1になる
2 位置ベクトルを利用して点の位置を決定する
- 2.1 直線と平面の交点による位置ベクトル
- 2.2 平面に下ろした垂線と平面との交点
3 位置ベクトルの性質を利用して空間ベクトルの問題を解く

空間ベクトルでの内分点、外分点、重心の公式

平面ベクトルに対して、\(z\)成分が加わると空間ベクトルになります。そのため平面ベクトルも空間ベクトルもほぼ同じ概念です。事実、空間ベクトルで位置ベクトルを利用するとき、内分点の公式、外分点の公式、重心の公式は平面ベクトルと同じです。

点Aの位置ベクトル\(\overrightarrow{a}\)と点Bの位置ベクトル\(\overrightarrow{b}\)について、線分ABを\(m:n\)に内分する位置ベクトル\(\overrightarrow{p}\)は以下になります。

\(\overrightarrow{p}=\displaystyle\frac{n\overrightarrow{a}+m\overrightarrow{b}}{m+n}\)

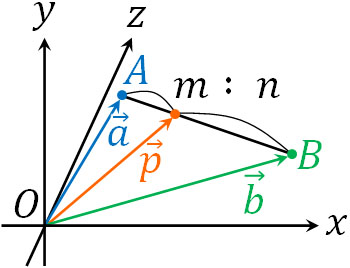
また、空間ベクトルでの外分点の公式は以下になります。

\(\overrightarrow{p}=\displaystyle\frac{-n\overrightarrow{a}+m\overrightarrow{b}}{m-n}\)

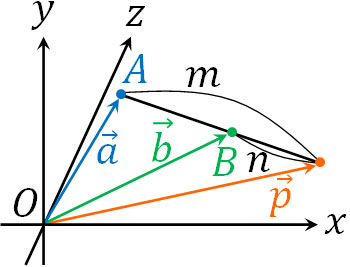
このように、平面ベクトルでの内分点・外分点の公式とまったく同じとわかります。重心Gを得る公式も同じであり、以下のようになります。

\(G=\displaystyle\frac{\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}}{3}\)

これが、平面ベクトルで位置ベクトルを理解している場合、空間ベクトルで覚えなければいけない内容がほとんどない理由です。

共線条件・共点条件は平面ベクトルと空間ベクトルで同じ

それだけでなく、共線条件・共点条件も平面ベクトルと空間ベクトルで同じです。同じ線上にベクトルが存在する場合、以下の関係が成り立ちます。

\(\overrightarrow{AP}=k\overrightarrow{AB}\)

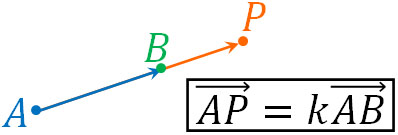
点A、点B、点Pが同じ直線上に存在するのであれば、\(\overrightarrow{AB}\)を実数倍することにより、\(\overrightarrow{AP}\)を得ることができます。

また位置ベクトルが同じ場合、同じ点であることを意味します。これを共点条件といいます。空間ベクトルで同じ点であることを表したい場合、位置ベクトルを利用しましょう。

共面条件では、係数を足すと1になる

なお、空間ベクトルでは共面条件が存在します。平面ベクトルでは線のみを考えればいいです。一方で空間ベクトルでは、立体図形で考える必要があるため、特定の面に存在する点を計算する必要があります。

平面ベクトルでは、点Aと点Bを通る直線を以下のように表すことができます。

\(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}\)
\(s+t=1\)

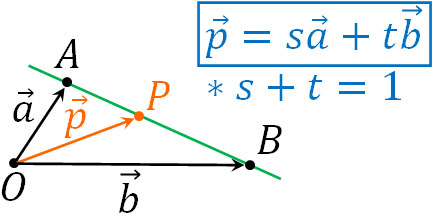
\(s+t=1\)、つまりベクトルの係数を足して1になる場合、2つの点を通る直線を表せます。言い換えると、点P（\(\overrightarrow{p}\)）は辺AB上のどこかに存在します。

「係数を足して1にする」という考え方は空間ベクトルでも重要です。それでは、空間ベクトルで係数を足して1になる場合、何を意味するのでしょうか。以下の条件を考えてみましょう。

\(\overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}+u\overrightarrow{c}\)
\(s+t+u=1\)

これは、点Pが「点A、点B、点Cを通る平面」の上に存在することを意味しています。

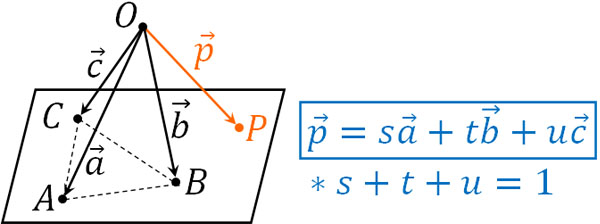
これが、空間ベクトルでの共面条件です。空間ベクトルで係数が1の場合、3つの点を通る面上に点Pが存在することになります。

位置ベクトルを利用して点の位置を決定する

それでは、ここまで解説した内容を利用して問題を解いてみましょう。公式を利用することにより、答えを得るのです。以下の問題の答えは何でしょうか。

四面体OBCDについて、\(\overrightarrow{OP}+3\overrightarrow{AP}\)\(+2\overrightarrow{BP}\)\(+6\overrightarrow{CP}\)\(=\overrightarrow{0}\)を満たす点Pはどのような点でしょうか。

まず、以下のように計算しましょう。

\(\overrightarrow{OP}+3\overrightarrow{AP}\)\(+2\overrightarrow{BP}\)\(+6\overrightarrow{CP}\)\(=\overrightarrow{0}\)

\(\overrightarrow{OP}+3(\overrightarrow{OP}-\overrightarrow{OA})\)\(+2(\overrightarrow{OP}-\overrightarrow{OB})\)\(+6(\overrightarrow{OP}-\overrightarrow{OC})\)\(=\overrightarrow{0}\)

\(12\overrightarrow{OP}-3\overrightarrow{OA}-2\overrightarrow{OB}\)\(-6\overrightarrow{OC}\)\(=\overrightarrow{0}\)

\(\overrightarrow{OP}=\displaystyle\frac{1}{12}(3\overrightarrow{OA}+2\overrightarrow{OB}\)\(+6\overrightarrow{OC})\)

ただ、ここまでの計算では点Pがどのような点なのかわかりません。そこで、以下のように変形しましょう。

\(\overrightarrow{OP}=\displaystyle\frac{1}{12}\)\(\left(5·\displaystyle\frac{3\overrightarrow{OA}+2\overrightarrow{OB}}{2+3}+6\overrightarrow{OC}\right)\)

こうして、点Pは線分ABを\(2:3\)に内分することと関係していることがわかります。次に、\(\displaystyle\frac{3\overrightarrow{OA}+2\overrightarrow{OB}}{2+3}=\overrightarrow{OD}\)としましょう。点D（\(\overrightarrow{OD}\)）は線分ABを\(2:3\)に内分する点です。そうすると、式は以下のようになります。

\(\overrightarrow{OP}=\displaystyle\frac{1}{12}\)\((5\overrightarrow{OD}+6\overrightarrow{OC})\)

\(\overrightarrow{OP}=\displaystyle\frac{11}{12}\)\(\left(\displaystyle\frac{5\overrightarrow{OD}+6\overrightarrow{OC}}{6+5}\right)\)

こうして、点Pは線分DCを\(6:5\)に内分することと関係していることがわかります。線分DCを\(6:5\)に内分する点をE（\(\overrightarrow{OE}\)）としましょう。また\(\displaystyle\frac{5\overrightarrow{OD}+6\overrightarrow{OC}}{6+5}=\overrightarrow{OE}\)であるため、以下のようになります。

\(\overrightarrow{OP}=\displaystyle\frac{11}{12}\overrightarrow{OE}\)

つまり線分ABを\(2:3\)に内分する点をD、線分DCを\(6:5\)に内分する点をEとすると、点Pは線分OEを\(11:1\)に内分する点であるとわかります。

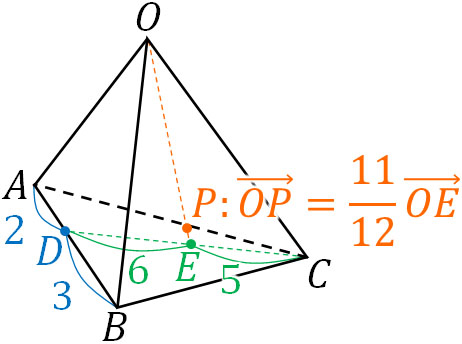
内分点の公式を利用することにより、式を変形することで点Pがどのような点なのか確認しましょう。

直線と平面の交点による位置ベクトル

空間ベクトルが関わる計算問題では、共線条件と共面条件を利用する問題がひんぱんに出題されます。特に共面条件は重要であり、係数を利用して問題を解きましょう。以下の問題の答えは何でしょうか。

四面体OABCについて、OAを\(2:1\)に内分する点をD、OBを\(2:1\)に内分する点をEとします。△ABCの重心をGとするとき、\(\overrightarrow{OG}\)と△DECとの交点をFとします。\(\overrightarrow{OA}\)、\(\overrightarrow{OB}\)、\(\overrightarrow{OC}\)を用いて\(\overrightarrow{OF}\)を表しましょう。

まず、図を作りましょう。以下のようになります。

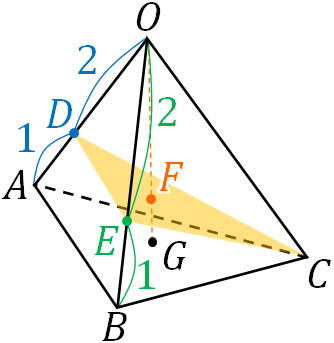
点Gは△ABCの重心であるため、位置ベクトルを利用して以下のように表せます。

\(\overrightarrow{OG}=\displaystyle\frac{\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}}{3}\)

また\(\overrightarrow{OF}\)を伸ばすと\(\overrightarrow{OG}\)になるため、\(\overrightarrow{OF}=k\overrightarrow{OG}\)です。つまり、以下のように\(\overrightarrow{OF}\)を表すことができます。

\(\overrightarrow{OF}=\displaystyle\frac{k}{3}\overrightarrow{OA}+\displaystyle\frac{k}{3}\overrightarrow{OB}+\displaystyle\frac{k}{3}\overrightarrow{OC}\)

なお、点Fは△DEC上に存在します。そこで共面条件を利用することにより、以下のように表すことができます。

\(\overrightarrow{OF}=s\overrightarrow{OD}+t\overrightarrow{OE}+u\overrightarrow{OC}\)
\(s+t+u=1\)

OAを\(2:1\)に内分する点がD、OBを\(2:1\)に内分する点がEであるため、この式を以下のように変形できます。

\(\overrightarrow{OF}=\displaystyle\frac{2s}{3}\overrightarrow{OA}+\displaystyle\frac{2t}{3}\overrightarrow{OE}+u\overrightarrow{OC}\)
\(s+t+u=1\)

同じベクトルであれば、係数は必ず同じになります。そこで、以下の2つの条件を利用して係数を確認しましょう。

\(\overrightarrow{OF}=\displaystyle\frac{k}{3}\overrightarrow{OA}+\displaystyle\frac{k}{3}\overrightarrow{OB}+\displaystyle\frac{k}{3}\overrightarrow{OC}\)
\(\overrightarrow{OF}=\displaystyle\frac{2s}{3}\overrightarrow{OA}+\displaystyle\frac{2t}{3}\overrightarrow{OE}+u\overrightarrow{OC}\)

言い換えると、以下の関係が成り立ちます。

\(\displaystyle\frac{k}{3}=\displaystyle\frac{2s}{3}\)
\(\displaystyle\frac{k}{3}=\displaystyle\frac{2t}{3}\)
\(\displaystyle\frac{k}{3}=u\)

整理すると、以下のようになります。

\(\displaystyle\frac{k}{2}=s\)
\(\displaystyle\frac{k}{s}=t\)
\(\displaystyle\frac{k}{3}=u\)

そこで、\(s+t+u=1\)へ代入しましょう。

\(s+t+u=1\)

\(\displaystyle\frac{k}{2}+\displaystyle\frac{k}{2}+\displaystyle\frac{k}{3}=1\)

\(8k=6\)

\(k=\displaystyle\frac{3}{4}\)

そこで、\(k=\displaystyle\frac{3}{4}\)を代入しましょう。

\(\overrightarrow{OF}=\displaystyle\frac{k}{3}\overrightarrow{OA}+\displaystyle\frac{k}{3}\overrightarrow{OB}+\displaystyle\frac{k}{3}\overrightarrow{OC}\)

\(\overrightarrow{OF}=\displaystyle\frac{1}{4}\overrightarrow{OA}+\displaystyle\frac{1}{4}\overrightarrow{OB}+\displaystyle\frac{1}{4}\overrightarrow{OC}\)

こうして、\(\overrightarrow{OA}\)、\(\overrightarrow{OB}\)、\(\overrightarrow{OC}\)を用いて\(\overrightarrow{OF}\)を表すことができました。

平面に下ろした垂線と平面との交点

次に、垂線を用いる場合の計算方法も学びましょう。四面体について、一つの頂点から平面に対して垂線を作る場合、以下の図になります。

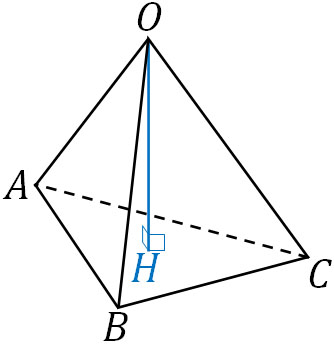
この図では、以下の関係がわかります。

\(OH⊥AB\)
\(OH⊥BC\)
\(OH⊥CA\)

垂直の場合、2つのベクトルの内積はゼロになります。また、点Hは点A、点B、点Cを含む平面上に存在します。つまり、以下の関係も成り立ちます。

\(OH⊥AH\)

平面上の点を利用してベクトルを作る場合、垂線に対して必ず垂直になります。この性質を利用することで計算しましょう。それでは、以下の問題の答えは何でしょうか。

4点O\((0,0,0)\)、A\((1,0,0)\)、B\((1,1,1)\)、C\((2,3,2)\)があります。点CからOABを含む平面に対して垂線を引き、平面との交点をHとします。点Hの座標を求めましょう。

まず、以下のように図を作りましょう。

ちなみに、空間ベクトルの問題を解くために図を作るとき、図は適当で問題ありません。正確に図を作るのは時間がかかるため、上図のような簡便な図を作りましょう。

なお点Hは平面上に存在します。平面上に存在するベクトルでは、2つのベクトルを用いて1つのベクトルを表現できます。そこで、\(\overrightarrow{OH}\)を以下のように表現しましょう。

\(\overrightarrow{OH}=s\overrightarrow{OA}+t\overrightarrow{OB}\)

\(\overrightarrow{OH}=(s+t,t,t)\)

こうして、点Hの座標は\((s+t,t,t)\)になるとわかりました。そのため、\(\overrightarrow{CH}\)は以下のようになります。

\(\overrightarrow{CH}=(s+t-2,t-3,t-2)\)

そこで、法線ベクトルを用いる場合に内積がゼロになる性質を利用して式を作りましょう。

・\(\overrightarrow{CH}·\overrightarrow{OA}=0\)より

\((s+t-2)×1+(t-3)×0\)\(+(t-2)×0\)\(=0\)

\(s=2-t\)

・\(\overrightarrow{CH}·\overrightarrow{OB}=0\)より

\((s+t-2)×1+(t-3)×1\)\(+(t-2)×1\)\(=0\)

\(s+3t-7=0\)

そこで、\(s=2-t\)を\(s+3t-7=0\)に代入しましょう。

\(s+3t-7=0\)

\((2-t)+3t-7=0\)

\(2t=5\)

\(t=\displaystyle\frac{5}{2}\)

\(t=\displaystyle\frac{5}{2}\)であるため、\(s=-\displaystyle\frac{1}{2}\)です。そのため、点Hの座標は\(\left(2,\displaystyle\frac{5}{2},\displaystyle\frac{5}{2}\right)\)です。こうして、点Hの座標を得ることができました。

参考までに、点Hの座標がわかればCHの長さ（\(|\overrightarrow{CH}|\)）を計算できます。また座標を用いて△OABの面積を計算できるため、四面体OABCの体積を計算することも可能です。CHは垂線であるため、三角錐の体積を得る公式を利用できるのです。