面積を計算する方法が積分です。そこで曲線について、定積分を用いて面積を計算できるようになりましょう。
\(x\)軸と曲線による面積を計算したい場合、\(y\)軸の値がプラスになるのか、それともマイナスになるのかによって符号を考えなければいけません。また2曲線の間の面積では、どちらの曲線で\(y\)軸の値が大きくなるのかを考えて計算する必要があります。
また積分を利用することにより、面積の最大値と最小値を計算できるようになる必要があります。ほかにも、式に絶対値を含む場合の積分についても計算方法を学びましょう。
それでは公式を利用してどのように積分し、面積を計算すればいいのでしょうか。曲線によって作られる面積の計算方法を解説していきます。
もくじ
曲線と\(x\)軸による面積を計算する
範囲を指定して積分することにより、面積を得ることができます。曲線と\(x\)軸の間に作られる面積について、範囲が\(a\)から\(b\)の場合、面積\(S\)を以下のように計算しましょう。
- \(S=\displaystyle \int_{a}^{b} f(x) dx\)
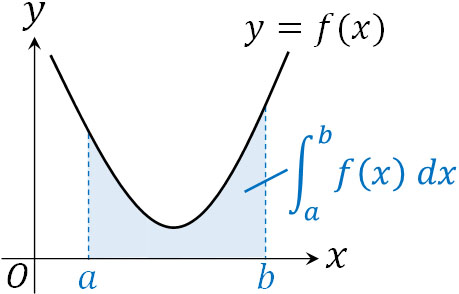
定積分を利用することにより、面積の計算が可能です。
ただ場合によっては、\(x\)軸の下側に関数が存在するケースもあります。\(a≦x≦b\)の範囲で\(y\)の値がマイナスの場合、定積分の計算をするときにマイナスを加えましょう。そのため、以下のように計算します。
- \(S=-\displaystyle \int_{a}^{b} f(x) dx\)
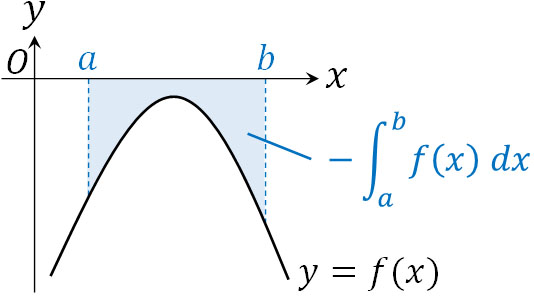
場合によっては、場所によって\(y\)軸の値がプラスになったり、マイナスになったりと変化することがあります。この場合、\(y\)軸の値がマイナスのときのみ、積分するときにマイナスを加えましょう。以下のようになります。
- \(S=\displaystyle \int_{a}^{b} f(x) dx\)\(-\displaystyle \int_{b}^{c} f(x) dx\)
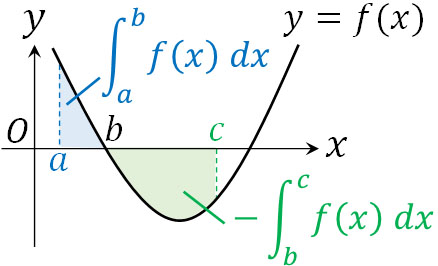
それでは以下の式について、\(-1≦x≦1\)のとき、曲線と\(x\)軸で囲まれた部分の面積を計算しましょう。
- \(y=x^2-3x\)
面積の計算では、グラフを描く必要があります。因数分解すると、\(y=x(x-3)\)となります。そのため、\(x\)軸との交点は\(0,3\)です。

それではグラフを利用して、\(y\)軸の値がプラスになるのか、それともマイナスになるのかを確認して式を作りましょう。
\(S=\displaystyle \int_{-1}^{0} (x^2-3x) dx\)\(-\displaystyle \int_{0}^{1} (x^2-3x) dx\)
\(S=\left[\displaystyle\frac{1}{3}x^3-\displaystyle\frac{3}{2}x^2\right]_{-1}^{0}\)\(-\left[\displaystyle\frac{1}{3}x^3-\displaystyle\frac{3}{2}x^2\right]_{0}^{1}\)
\(S=0-\left(-\displaystyle\frac{1}{3}-\displaystyle\frac{3}{2}\right)\)\(-\left(\displaystyle\frac{1}{3}-\displaystyle\frac{3}{2}\right)+0\)
\(S=\displaystyle\frac{11}{6}+\displaystyle\frac{7}{6}\)
\(S=3\)
こうして、面積は\(S=3\)とわかりました。
2曲線の間の面積と積分
それでは曲線と\(x\)軸によって作られる面積ではなく、2曲線の間の面積はどのように計算すればいいのでしょうか。先ほどとは異なり、\(y\)軸の符号を確認する必要はなく、2つの曲線について、引き算をして積分すればいいです。
例えば\(a\)から\(b\)の範囲で\(f(x)>g(x)\)である2つの関数があるとします。この場合、2つの関数によって作られる\(a\)から\(b\)までの面積は以下のように計算できます。
- \(S=\displaystyle \int_{a}^{b} \{f(x)-g(x)\} dx\)
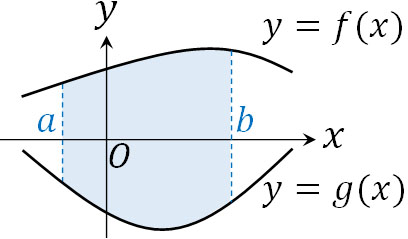
それでは、以下の問題を解いてみましょう。
- \(y=x^2\)と\(y=-x^2-x+1\)によって囲まれる面積を計算しましょう。
まず、2つの曲線の交点を計算しましょう。
\(x^2=-x^2-x+1\)
\(2x^2+x-1=0\)
\((2x-1)(x+1)=0\)
こうして\(x=-1,\displaystyle\frac{1}{2}\)のとき、2曲線は交わるとわかります。
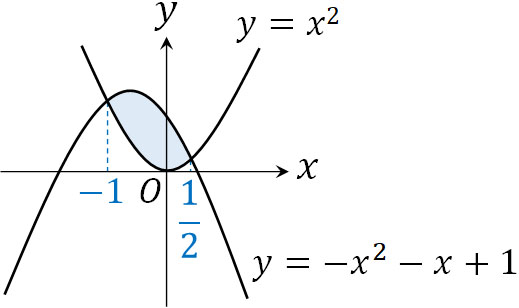
また、\(-1≦x≦\displaystyle\frac{1}{2}\)では\(y=-x^2-x+1\)が\(y=x^2\)よりも上にあります。そこで、以下のように計算しましょう。
\(S=\displaystyle \int_{-1}^{\frac{1}{2}} \{(-x^2-x+1)-(x^2)\} dx\)
\(S=\displaystyle \int_{-1}^{\frac{1}{2}} (-2x^2-x+1) dx\)
\(S=\left[-\displaystyle\frac{2}{3}x^3-\displaystyle\frac{1}{2}x^2+x\right]_{-1}^{\frac{1}{2}}\)
\(S=\left(-\displaystyle\frac{1}{12}-\displaystyle\frac{1}{8}+\displaystyle\frac{1}{2}\right)-\left(\displaystyle\frac{2}{3}-\displaystyle\frac{1}{2}-1\right)\)
\(S=\displaystyle\frac{27}{24}\)
\(S=\displaystyle\frac{9}{8}\)
こうして、2曲線の間の面積を求めることができました。2つの曲線を利用して面積を計算するとき、上から下を引いて積分しましょう。
積分による三次関数の面積の計算
積分による計算方法は三次曲線(三次関数)であっても同様です。グラフを描き、上から下を引くことによって計算しましょう。また三次曲線と\(x\)軸による面積では、\(y\)軸の値がプラスなのか、それともマイナスなのかを確認しましょう。
例題として、以下の問題を解いてみましょう。
- \(y=x^3-x\)と\(x\)軸で囲まれた面積を求めましょう。
\(x\)軸との交点を確認すると以下のようになります。
\(x^3-x=0\)
\(x(x^2-1)=0\)
\(x(x-1)(x+1)=0\)
\(x=-1,0,1\)
そのため、以下の図を作ることができます。
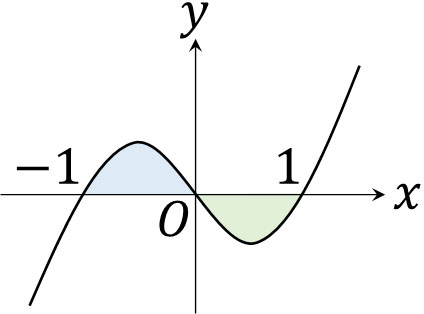
計算方法はこれまで説明したやり方と同じです。積分を利用して計算するものの、\(y\)の値がマイナスになる場合、マイナスを加えて積分をしましょう。
\(S=\displaystyle \int_{-1}^{0} (x^3-x) dx\)\(-\displaystyle \int_{0}^{1} (x^3-x) dx\)
\(S=\left[\displaystyle\frac{1}{4}x^4-\displaystyle\frac{1}{2}x^2\right]_{-1}^{0}\)\(-\left[\displaystyle\frac{1}{4}x^4-\displaystyle\frac{1}{2}x^2\right]_{0}^{1}\)
\(S=0-\left(\displaystyle\frac{1}{4}-\displaystyle\frac{1}{2}\right)\)\(-\left(\displaystyle\frac{1}{4}-\displaystyle\frac{1}{2}\right)+0\)
\(S=\displaystyle\frac{1}{2}\)
こうして、面積を計算することができました。
放物線と2つの接線によって作られる面積
なお面積の計算をするとき、微分をすることによって傾きを計算するケースがひんぱんにあります。そのため積分だけでなく、微分を利用することによって面積を計算できるようになりましょう。微分を利用して面積を計算するケースとしては、放物線と接線によって作られる面積が挙げられます。
接線の方程式を求めた後、放物線と接線によって作られるそれぞれの面積を計算することで解答できます。それでは、以下の問題を解いてみましょう。
- 点\((1,-3)\)を通る\(y=x^2\)の接線について、接線と放物線で囲まれる部分の面積を求めましょう。
傾きを得るためには微分する必要があります。そこで\(y=x^2\)を微分すると、\(y’=2x\)になります。放物線上の接点を\((t,t^2)\)とすると、接線の傾きは\(y’=2t\)です。そのため、接線の方程式は以下のようになります。
- \(y-t^2=2t(x-t)\)
なお接線は\((1,-3)\)を通るため、代入しましょう。
\(-3-t^2=2t(1-t)\)
\(t^2-2t-3=0\)
\((t+1)(t-3)=0\)
\(t=-1,3\)
\(t=-1,3\)であるため、接線の方程式は以下の2つです。
- \(y=-2x-1\)
- \(y=6x-9\)
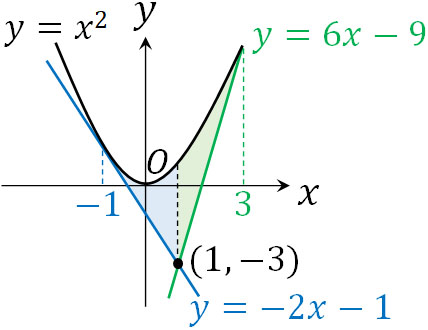
そこで、2つの面積を出して足しましょう。以下のように計算します。
\(S=\displaystyle \int_{-1}^{1} \{x^2-(-2x-1)\} dx\)\(+\displaystyle \int_{1}^{3} \{x^2-(6x-9)\} dx\)
\(S=\displaystyle \int_{-1}^{1} (x^2+2x+1) dx\)\(+\displaystyle \int_{1}^{3} (x^2-6x+9) dx\)
\(S=\left[\displaystyle\frac{1}{3}x^3+x^2+x\right]_{-1}^{1}\)\(+\left[\displaystyle\frac{1}{3}x^3-3x^2+9x\right]_{1}^{3}\)
\(S=\left(\displaystyle\frac{1}{3}+1+1\right)\)\(-\left(-\displaystyle\frac{1}{3}+1-1\right)\)\(+(9-27+27)\)\(-\left(\displaystyle\frac{1}{3}-3+9\right)\)
\(S=\displaystyle\frac{16}{3}\)
微分を利用して接線の方程式を計算し、それぞれの面積を得ることによって答えを出すことができました。
絶対値を含む積分の計算
計算問題によっては、絶対値を含むケースがあります。絶対値を利用する場合、答えは必ずプラスになります。そのため絶対値の中がマイナスの場合、プラスにするため、マイナスを加えて絶対値を外さなければいけません。
そこで絶対値の中がプラスになるのか、それともマイナスになるのか確認して絶対値を外し、それぞれ積分しましょう。以下の問題の答えは何でしょうか。
- \(\displaystyle \int_{-2}^{1} |x^2-x| dx\)
グラフを描くと以下のようになります。

そこで、以下のように計算しましょう。
\(\displaystyle \int_{-2}^{0} (x^2-x) dx\)\(+\displaystyle \int_{0}^{1} (-x^2+x) dx\)
\(=\left[\displaystyle\frac{1}{3}x^3-\displaystyle\frac{1}{2}x^2\right]_{-2}^{0}\)\(+\left[-\displaystyle\frac{1}{3}x^3+\displaystyle\frac{1}{2}x^2\right]_{0}^{1}\)
\(=0-\left(-\displaystyle\frac{8}{3}-2\right)\)\(+\left(-\displaystyle\frac{1}{3}+\displaystyle\frac{1}{2}\right)-0\)
\(=\displaystyle\frac{29}{6}\)
こうして、絶対値を含む計算問題を解くことができました。
なお、絶対値を含む定積分の計算というのは、関数と\(x\)軸によって作られる面積の計算と式が同じです。そのため\(\displaystyle \int_{-2}^{1} |x^2-x| dx\)というのは、\(-2≦x≦1\)の範囲について\(y=x^2-x\)と\(x\)軸によって作られる面積の計算と同じです。
定積分による面積の計算を学べば、絶対値を含む場合の計算を行えるようになります。
2つの交点で利用できる6分の1公式
なお定積分を利用して面積の計算をするとき、6分の1公式を利用することができます。この公式を知っている場合、計算スピードが速くなります。2つの接点を利用して面積を計算するとき、6分の1公式が役立ちます。例えば、以下のケースです。
- 直線と放物線による面積
- 放物線と放物線による面積
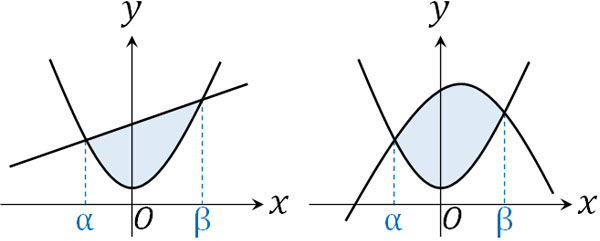
2つの方程式が交点をもつ場合、連立させることによって\(x\)軸の交点座標を得ることができます。\(x\)軸の交点座標を\(α\)、\(β\)とすると、以下の式を得ることができます。
- \((x-α)(x-β)=0\)
2つの方程式の交点(連立させた式)について、\(x\)の答えが\(α\)、\(β\)であるため、この式を作れるのは問題なく理解できると思います。
また交点と定積分を利用して面積を計算するとき、グラフの上にある式からグラフの下にある式を引きます。これはつまり、連立させて計算することにより、\(y=(x-α)(x-β)\)の式を作れることを意味しています。このとき、以下が6分の1公式になります。
- \(\displaystyle \int_{α}^{β} (x-α)(x-β) dx=-\displaystyle\frac{1}{6}(β-α)^3\)
この公式を証明すると以下のようになります(証明方法を覚える必要はありません)。
\(\displaystyle \int_{α}^{β} (x-α)(x-β) dx\)
\(=\displaystyle \int_{α}^{β} (x-α)\{(x-α)-(β-α)\} dx\)
\(=\displaystyle \int_{α}^{β} \{(x-α)^2-(β-α)(x-α)\} dx\)
\(=\left[\displaystyle\frac{1}{3}(x-α)^3-(β-α)·\displaystyle\frac{1}{2}(x-α)^2\right]_{α}^{β}\)
\(=\displaystyle\frac{1}{3}(β-α)^3-\displaystyle\frac{1}{2}(β-α)^3\)
\(=-\displaystyle\frac{1}{6}(β-α)^3\)
※この計算を理解するためには、かっこ内に変数を含む場合の積分を知っている必要があります。
それでは、実際に6分の1公式を利用して計算してみましょう。先ほど、以下の問題を解きました。
- \(y=x^2\)と\(y=-x^2-x+1\)によって囲まれる面積を計算しましょう。
先ほどの計算より、2曲線の\(x\)軸の交点は\(x=-1,\displaystyle\frac{1}{2}\)です。
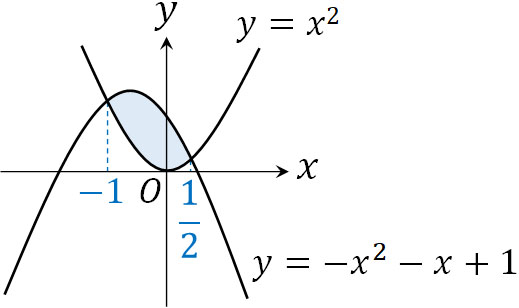
そこで6分の1公式を利用すると、以下のように計算できます。
\(S=\displaystyle \int_{-1}^{\frac{1}{2}} \{(-x^2-x+1)-(x^2)\} dx\)
\(S=\displaystyle \int_{-1}^{\frac{1}{2}} (-2x^2-x+1) dx\)
\(S=-\displaystyle \int_{-1}^{\frac{1}{2}} (2x^2+x-1) dx\)
\(S=-\displaystyle \int_{-1}^{\frac{1}{2}} (x+1)(2x-1) dx\)
\(S=-2\displaystyle \int_{-1}^{\frac{1}{2}} (x+1)(x-\displaystyle\frac{1}{2}) dx\)
\(S=2×\displaystyle\frac{1}{6}\left(\displaystyle\frac{1}{2}+1\right)^3\)
\(S=2×\displaystyle\frac{1}{6}×\displaystyle\frac{27}{8}\)
\(S=\displaystyle\frac{9}{8}\)
こうして、先ほどと同じ答えを得ることができました。注意点として、6分の1公式は積分記号内にある\(x\)の係数が1である必要があります。そのため\(-\displaystyle \int_{-1}^{\frac{1}{2}} (x+1)(2x-1) dx\)を\(-2\displaystyle \int_{-1}^{\frac{1}{2}} (x+1)(x-\displaystyle\frac{1}{2}) dx\)へ変換する必要があります。
定積分による面積の最大値・最小値
定積分を利用して面積を計算するとき、変数が含まれることにより、面積が変化することがあります。このとき、面積の最大値または最小値を計算できるようになりましょう。
定積分をした後、式を確認することで最大値または最小値となる値を得ます。それでは、以下の問題の答えは何でしょうか。
- 点\((1,2)\)を通る直線と放物線\(y=x^2\)が2点で交わるとき、直線と放物線で囲まれる面積\(S\)の最小値を計算しましょう。
点\((1,2)\)を通る直線の傾きを\(m\)とすると、以下のように直線の方程式を表すことができます。
\(y-2=m(x-1)\)
\(y=mx-m+2\)
\(y=mx-m+2\)と\(y=x^2\)の交点について、\(x\)座標はわかりません。そこで、交点の\(x\)座標を\(α\)と\(β\)にします。
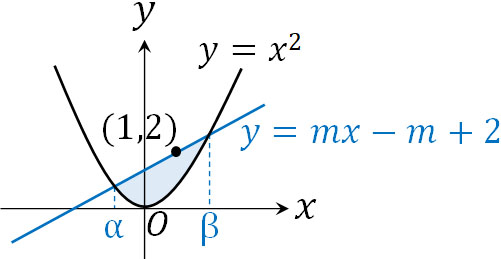
また、グラフの上にある関数からグラフの下にある関数を引きます。そのため、定積分で利用する関数は以下になります。
\(mx-m+2-(x^2)\)
\(=-x^2+mx-m+2\)
また直線と放物線による2つの接点を利用して面積を計算するため、6分の1公式を利用することができます。交点の\(x\)座標は\(α\)と\(β\)であるため、以下のように定積分を利用して計算できます。
\(S=\displaystyle \int_{α}^{β} (-x^2+mx-m+2) dx\)
\(S=-\displaystyle \int_{α}^{β} (x^2-mx+m-2) dx\)
\(S=-\displaystyle \int_{α}^{β} (x-α)(x-β) dx\)
\(S=\displaystyle\frac{1}{6}(β-α)^3\)
それでは、\(β-α\)を計算しましょう。\(x^2-mx+m-2=0\)について、判別式を\(D\)とすると、解の公式より答えは以下になります。
- \(x=\displaystyle\frac{m±\sqrt{D}}{2}\)
そのため、以下のように\(β-α\)を計算しましょう。
\(β-α=\displaystyle\frac{m+\sqrt{D}}{2}-\displaystyle\frac{m-\sqrt{D}}{2}\)
\(β-α=\sqrt{D}\)
そこで、判別式\(D\)を計算しましょう。
\(D=m^2-4(m-2)\)
\(D=m^2-4m+8\)
そのため、\(β-α=\sqrt{m^2-4m+8}\)です。この結果から、どのように最小値を計算すればいいでしょうか。\(S=\displaystyle\frac{1}{6}(β-α)^3\)が最小になるためには、\(β-α\)が最小になればいいです。
二次関数で最小値を得るためには、二乗を作ればいいです。そこで、以下のように式を変形しましょう。
\(β-α=\sqrt{m^2-4m+8}\)
\(β-α=\sqrt{(m-2)^2+4}\)
つまり、\(m=2\)のとき\(β-α=2\)となり、面積は最小値となります。また\(β-α=2\)を代入すると、\(S=\displaystyle\frac{4}{3}\)となります。こうして、定積分と6分の1公式を利用して面積の最小値を得ることができました。
積分を利用して面積を計算する
私たちが数学で積分を学ぶのは、面積を計算できるようになるためです。特に力学や土木、航空宇宙、量子力学など、物理では積分がひんぱんに利用されます。そこで、どのように面積を計算すればいいのか学びましょう。
定積分をするとき、\(y\)の値がプラスなのかマイナスなのかによって、マイナスを加えて定積分をしなければいけないのかどうかが変わります。また二つの線を用いて積分をする場合、どちらがグラフの上側になるのか確認して面積を計算しましょう。このとき、6分の1公式を覚えていると計算が速いです。
場合によっては、絶対値を含む定積分の計算が出題されます。ただ絶対値を含む場合の計算というのは、曲線と\(x\)軸によって作られる面積の計算と考え方が同じです。
面積の計算では、応用問題もひんぱんに出されます。その中でも面積の最大値と最小値は最も一般的な問題であるため、解けるようにしましょう。数学で積分は重要な分野であるため、どのように計算すればいいのか理解する必要があります。






