統計学で学ぶ分野の一つが超幾何分布です。幾何分布とはまったく異なる分布であるため、幾何分布とは異なる概念として超幾何分布を学びましょう。
数式を眺めても、超幾何分布を理解できるようになることはありません。そこで、数式が何を意味しているのか理解する必要があります。
なお超幾何分布では期待値(平均)や分散を出すことができます。超幾何分布での期待値や分散の公式を導き出せるようになる必要はないものの、二項分布で期待値や分散を得る公式との違いを理解しましょう。
それでは、どのような場面で超幾何分布が利用されるのでしょうか。また、特徴には何があるのでしょうか。超幾何分布の概念や期待値・分散の出し方、二項分布との違いを含めて解説していきます。
もくじ
超幾何分布の概念と意味
二者択一のとき、超幾何分布を利用します。つまり、「結果が2つしかないとき、超幾何分布を用いることができる」と考えましょう。
どのような場面で超幾何分布を活用するかというと、二者択一の中でも、試行を繰り返すことによって発生確率が変わる場面で利用されます。
超幾何分布では合計\(N\)、目的物の数\(M\)、取り出すサンプル数\(n\)の3つを利用します。例えば、以下のケースで利用されるのが超幾何分布です。
- 合計\(N\)個のクジがあり、そのうち\(M\)個が当たりです。この中から\(n\)個を取り出す場合、当たりを引く確率はいくらでしょうか。
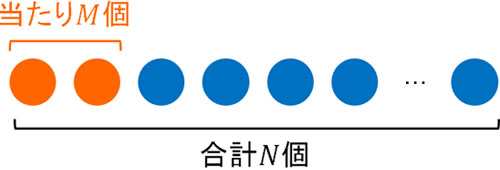
この場合、結果は当たり、またははずれの2つです。また試行回数を増やすごとに当たりを引く確率は変わります。例えばはずれクジを引いた場合、当たりを引く確率は高くなります。コインやサイコロのように、確率が同一の試行ではありません。このような確率分布が超幾何分布です。
確率質量関数の公式
それでは、超幾何分布で確率質量関数(確率を得る公式)はどのようになるのでしょうか。まずは具体例を利用して考えましょう。
先ほどの例題について、以下のケースを考えましょう。
- 合計8個のクジがあり、そのうち2個が当たりです。この中から3個を取り出し、当たりを1個引く場合、当たりを引く確率はいくらでしょうか。
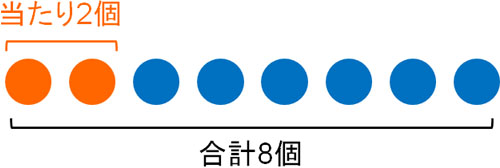
確率を計算するためには、分母に全体の数を置く必要があります。合計8個のうち、3個を取り出すため、分母は\(_8C_3\)です。
次に、当たりを1個引く場面を想定しましょう。当然、当たりを引くのが0個、1個、2個では確率はそれぞれ異なります。ここでは問題文の通り、当たりクジを1個引くというわけです。
当たり2個のうち、1個を選ぶので\(_2C_1\)です。またはずれ6個のうち、2個を選ぶので\(_6C_2\)です。そのため、以下の式によって確率を計算できます。
\(\displaystyle\frac{_2C_1×_6C_2}{_8C_3}≒0.536\)
確率の出し方を理解している人であれば、特に問題なく確率を計算できると思います。
ここまでの内容を踏まえ、超幾何分布で確率を得る公式を確認しましょう。超幾何分布の確率質量関数は以下になります。
- \(\displaystyle\frac{_MC_x×_{N-M}C_{n-x}}{_NC_n}\)
※\(x\)は当たりクジを引く数
最初にこの公式を見ると、多くの人は理解することができません。ただ今回、超幾何分布の確率質量関数を提示する前に例題を確認しました。先ほどの例題を数式に置き換えると、このような公式になります。簡単な例題を確認後、確率質量関数を学べば内容は難しくないことがわかります。
超幾何分布で期待値(平均)と分散を求める公式
次に超幾何分布の期待値(平均)を求めましょう。超幾何分布の期待値\(E(X)\)を出すとき、以下の公式を利用します。
- \(E(X)=\displaystyle\frac{nM}{N}\)
公式を出す計算過程は非常に複雑なので省きます。また分散\(V(X)\)については、以下の公式を利用して計算することができます。
- \(V(X)=\displaystyle\frac{nM}{N}\left(1-\displaystyle\frac{M}{N}\right)\)\(\left(\displaystyle\frac{N-n}{N-1}\right)\)
期待値や分散の公式を出す過程は複雑なので、興味のある人は大学の教科書を用いて学習してみてください。
二項分布と超幾何分布の関係と違い
それでは、先ほどの公式は何を意味しているのでしょうか。二者択一(結果が2つ)の分布として、二項分布が知られています。二項分布と超幾何分布は性質が似ています。そこで二項分布と超幾何分布の違いを理解し、公式の関係性を学びましょう。
超幾何分布では\(\displaystyle\frac{M}{N}\)に着目しましょう。分母が合計\(N\)であり、分子が当たりクジ\(M\)です。つまり、当たりクジを引く確率を表しています。二項分布では、\(\displaystyle\frac{M}{N}=p\)と表しました。そこで、以下のように先ほどの公式を変換してみましょう。
- \(E(X)=np\)
- \(V(X)=np(1-p)\left(\displaystyle\frac{N-n}{N-1}\right)\)
このように式を変えると、二項分布で期待値(平均)や分散を得る公式と同じ、または似ていることがわかります。二項分布で期待値\(E(X)\)と分散\(V(X)\)を得る公式は以下になります。
- \(E(X)=np\)
- \(V(X)=np(1-p)\)
つまり二項分布と超幾何分布で期待値や分散の公式を比較すると、\(\left(\displaystyle\frac{N-n}{N-1}\right)\)の部分が違うだけであるとわかります。
なお二項分布の場合、同じ試行を繰り返します。一方で超幾何分布の場合、試行を繰り返すと当たりクジを引く確率が変わります。はずれクジを何度も引くと、その分だけ当たりクジを引きやすくなるのです。
参考までに、\(N=∞\)の場合は\(\left(\displaystyle\frac{N-n}{N-1}\right)=1\)になります。例えば合計100万個のうち、当たりクジが1個含まれており、10回クジを引くとします。この場合、合計\(N\)が非常に大きいので、取り出す個数\(n\)を無視できます。
\(\left(\displaystyle\frac{N-n}{N-1}\right)=1\)の場合、超幾何分布の公式は分散を含めて二項分布と一致します。合計\(N\)が非常に大きい場合、超幾何分布を二項分布へ近似できるのです。
数億円の超高額なお金が当たる宝くじというのは、超幾何分布ではあるものの、合計\(N\)が非常に大きいので二項分布とみなすことができます。
なお一般的には、\(\displaystyle\frac{n}{N}≤0.1\)の場合は超幾何分布を二項分布へ近似できます。つまり全体の数\(N\)に対して、抜き取る数\(n\)の割合が0.1以下(10%以下)の場合、超幾何分布を二項分布とみなして計算して問題ありません。
ポアソン分布と超幾何分布の関係
なお超幾何分布が二項分布と似ていることから、場合によってはポアソン分布に近似することもできます。ポアソン分布は発生確率が非常に低いイベントに対して利用できます。
ポアソン分布を利用できる条件としては以下があります。
- \(\displaystyle\frac{x}{n}≤0.1\)
つまり抽出したサンプル\(n\)のうち、当たりクジの割合が0.1以下(10%以下)の場合はポアソン分布に近似できます。つまり超幾何分布、二項分布、ポアソン分布に対して以下の関係性があります。
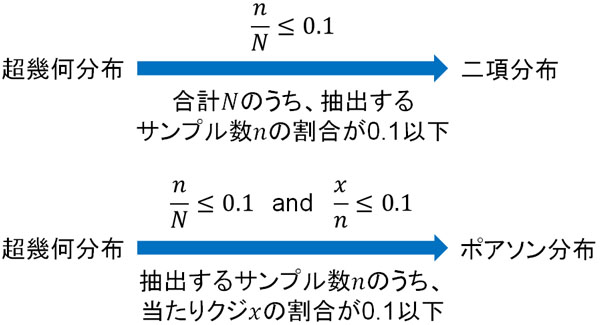
高額当選が可能な宝くじでは、多くのクジを購入したとしても当選確率は非常に低いです。そのため宝くじというのは、超幾何分布ではあるものの、ポアソン分布にも近似できるのです。
ここまでの内容を理解することは重要です。超幾何分布について、多くの場面で二項分布やポアソン分布への近似を利用できるからです。
例えば工場で商品を製造する場面であれば、一般的に不良品の発生確率は低いです。そのため、超幾何分布をポアソン分布とみなして統計処理しても問題ありません。
月の合計生成品\(N\)の中には、不良品\(M\)が含まれています。その中から任意のサンプル\(n\)を取り出すとき、不良品の個数\(x\)を確認するのです。本来は超幾何分布を利用するものの、不良品の発生確率が非常に低い場合、計算が大変な超幾何分布ではなくポアソン分布を利用できるのです。
超幾何分布の概念を学び、二項分布との違いを理解する
統計学で学ぶ超幾何分布というのは、高校数学を学んでいる人であれば簡単に概念を理解できます。公式をみても理解するのは難しいものの、例題を利用すれば公式の意味を把握できるというわけです。
なお超幾何分布で重要なのは、確率の計算ができるだけでなく、期待値や分散の意味を理解することにあります。超幾何分布と二項分布は親せきです。期待値を得る公式が同じであり、分散を得る公式は似ています。
また場合によっては、超幾何分布を二項分布やポアソン分布へ近似することも可能です。条件を満たしている場合、超幾何分布を二項分布やポアソン分布とみなして確率を計算しても問題ありません。
超幾何分布にはこれらの性質があります。母集団の中からサンプルを抽出するケースはひんぱんにあります。そうしたとき、超幾何分布を利用して確率や期待値、分散の計算をしましょう。






