相関関係を確認するとき、ピアソンの相関係数が最も一般的です。ただスピアマンの順位相関係数を利用することによって、相関関係を確認することもあります。
スピアマンの順位相関係数では、名前の通り順位を利用することで相関があるかどうかを確認します。このとき、ノンパラメトリック検定では順位を利用することで検定します。つまり、スピアマンの順位相関係数はノンパラメトリックによる手法です。
それでは、どのようにスピアマンの順位相関係数を利用すればいいのでしょうか。また、ピアソンの相関係数との違いには何があるのでしょうか。
スピアマンの順位相関係数について、順位を利用することでどのように相関関係を表すのか解説していきます。
もくじ
ピアソンの相関係数とスピアマンの順位相関係数の違い
一般的には、相関はピアソンの相関係数を指します。ピアソンの相関係数が最も一般的な手法と理解しましょう。
ただ、ピアソンの相関係数はデータが正規分布していることが前提です。母集団が正規分布している場合に利用可能な方法がパラメトリック法です。多くのデータは正規分布しているため、パラメトリック法であるピアソンの相関係数が利用されるのです。
一方で、データの中には正規分布ではないケースがあります。一つの山をもつ左右対称の形でなかったり、外れ値が含まれていたりする場合、正規分布ではありません。
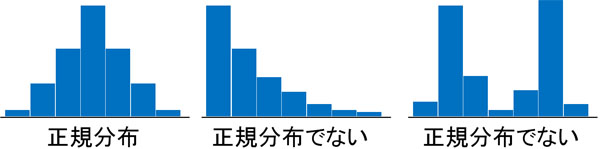
この場合、ピアソンの相関係数を利用することができません。ピアソンの相関係数はパラメトリック法だからです。
そこで統計学では、正規分布していなかったとしても利用できる統計処理法が存在します。こうした方法をノンパラメトリック法といいます。
スピアマンの順位相関係数はノンパラメトリック法になります。そのため母集団やデータが正規分布していなかったとしても、問題なく利用することができます。例えば外れ値が含まれていたとしてもスピアマンの順位相関係数は有効です。
パラメトリック法とノンパラメトリック法では、データとの相関係数が異なる
それでは相関係数を出すとき、ピアソンの相関係数(パラメトリック)とスピアマンの順位相関係数(ノンパラメトリック)では、どのような違いがあるのでしょうか。
相関係数rというのは、相関が強い場合は\(r=1\)に近づきます。一方で相関がない場合、\(r=0\)に近づきます。これは、ピアソンの相関係数でもスピアマンの順位相関係数でも同様です。
ただ、ピアソンの相関係数ではデータの場所が重要なのに対して、スピアマンの順位相関係数では順位が重要になります。そのため、データと相関係数の関係性が異なります。例えば、以下のようになります。

直線の場合、ピアソンの相関係数でもスピアマンの順位相関係数でも、相関係数rは1になります。つまり、非常に相関が強いです。
一方で直線ではない場合、ピアソンの相関係数だと、相関係数rの値は1よりも小さくなります。これについては、問題なく理解できると思います。
一方でスピアマンの順位相関係数だと、上図の場合、直線でなかったとしても相関係数rは1です。この理由として、ノンパラメトリック法では位置を考慮しないからです。そうではなく、順番を利用して判定します。以下のように、点の位置はズレているものの順番は同じです。
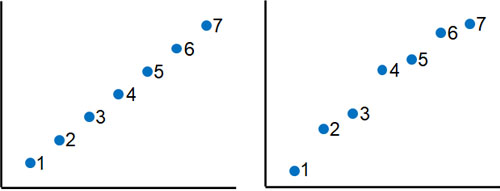
順番が変わらないため、スピアマンの順位相関係数では相関係数が1というわけです。
なお右肩上がりの場合、スピアマンの順位相関係数では相関係数rが1となります。一方で右肩下がりのグラフだと、相関係数rは-1となります。また順番がバラバラな場合、相関係数rは0です。
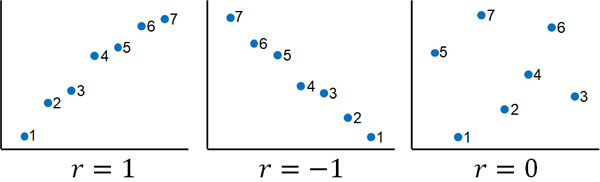
このようにスピアマンの順位相関係数では、順位による相関関係を知ることができます。
直線でなくても問題なく、外れ値があっても利用できる
先ほどの図をみればわかる通り、スピアマンの順位相関係数では直線でなくても利用できます。点の配置が右肩上がり(または右肩下がり)の場合、強い相関関係となります。ピアソンの相関係数では、直線のみ適用可能です。一方でスピアマンの順位相関係数では、曲線であっても利用できるのです。
一方、グラフの形が途中で折れ曲がる場合、強い相関関係とはなりません。曲線のグラフであっても、強い相関を得るためには右肩上がり(または右肩下がり)のグラフである必要があります。
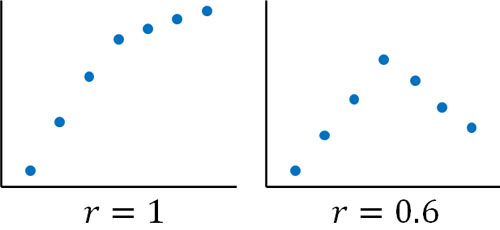
いずれにしても、直線でなくても利用できるのがスピアマンの順位相関係数の利点です。
またパラメトリック法とは異なり、ノンパラメトリック法では外れ値による影響を受けません。外れ値が含まれていると、パラメトリック法では正しい結果を得ることができません。一方でノンパラメトリック法の場合、外れ値が含まれていても問題ないのです。

ピアソンの相関係数は外れ値に弱いです。一方、スピアマンの順位相関係数は外れ値が含まれていても相関係数に影響はありません。
統計量(順位相関係数)Rsを求める概念
それでは、実際に順位相関係数Rsを求めてみましょう。このとき、どのようにして統計量Rsを計算すればいいのでしょうか。
ここまで解説した通り、スピアマンの順位相関係数では順位を利用します。そこで\(x\)と\(y\)について、順番をつけましょう。例えば広告費と売上の関係について、以下の表を得たとします。
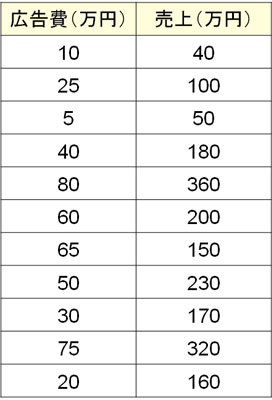
この表を利用して、スピアマンの順位相関係数で相関関係を確認しましょう。帰無仮説と対立仮説は以下のようになります。
- 帰無仮説:広告費と売上に相関はない
- 対立仮説:広告費と売上に相関がある
スピアマンの順位相関係数を利用する場合、まず以下のように順位をつけましょう。
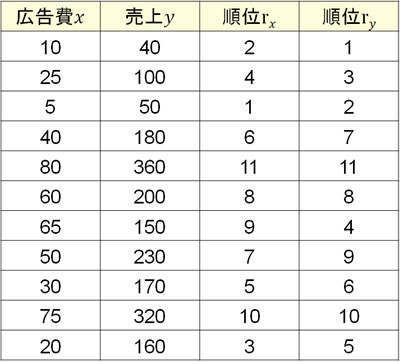
その後、\(x\)から\(y\)を引くことで順位差\(d\)を求めます。ただ順位差にはプラスとマイナスがあるため、すべてプラスにするため二乗します。
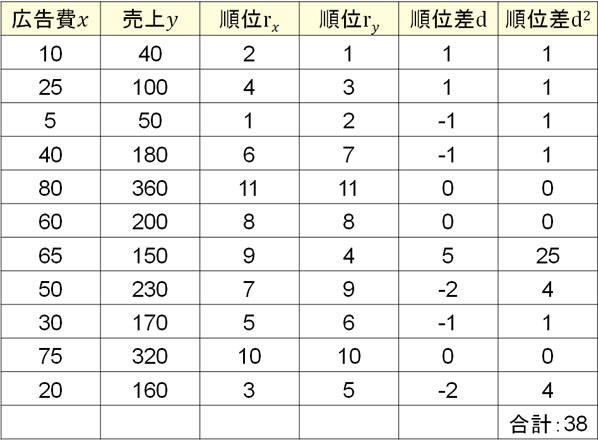
相関がある場合、\(x\)と\(y\)の順位は同じなので順位差\(d\)は0になります。一方で相関していない場合、\(x\)と\(y\)の順位差は大きく異なります。つまり、順位差\(d\)の値は大きくなります。スピアマンの順位相関係数では、順位差\(d\)を利用することで相関があるかどうかを確認するのです。
順位相関係数Rsを得る2つの計算方法と公式
次に順位相関係数を計算しましょう。スピアマンの順位相関係数では、2つの計算方法があります。どちらの方法を利用しても問題ありません。
・計算方法1
順位差の二乗d2やサンプル数\(n\)がわかったら、以下の公式に代入して統計量Rsを計算しましょう。
\(R_s=1-\displaystyle\frac{6\displaystyle\sum{d^2}}{n^3-n}\)
先ほど、順位差を二乗してすべて足すと38になると計算しました。また、サンプル数\(n\)は11です。そのため、以下の計算になります。
\(R_s=1-\displaystyle\frac{6×38}{11^3-11}≒0.83\)
こうして、相関係数は0.83であるとわかります。
・計算方法2
スピアマンの順位相関係数では、もう一つの計算方法があります。特に「同順位(同じ値)が多い標本」だと、先ほど解説した公式では誤差が大きくなるため、今回の計算方法を利用します。
この方法では偏差平方和(Sxx,Syy)と偏差積和(Sxy)を計算します。それぞれの偏差平方和と偏差積和は以下の公式によって計算できます。
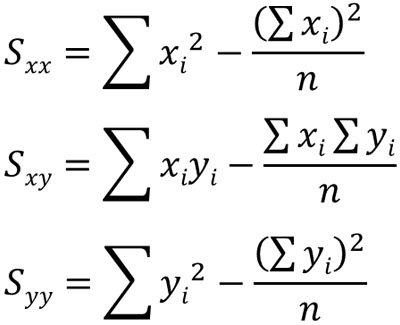
そこで以下の表を作り、偏差平方和と偏差積和を計算しましょう。
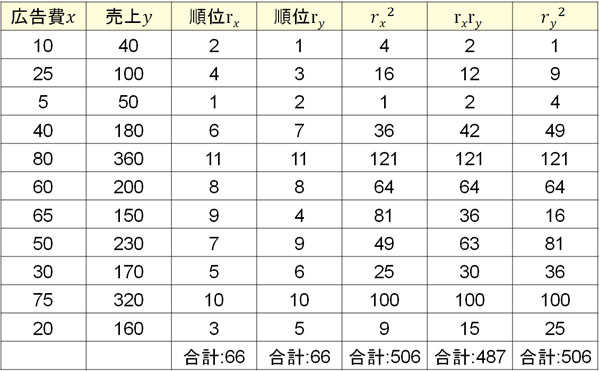
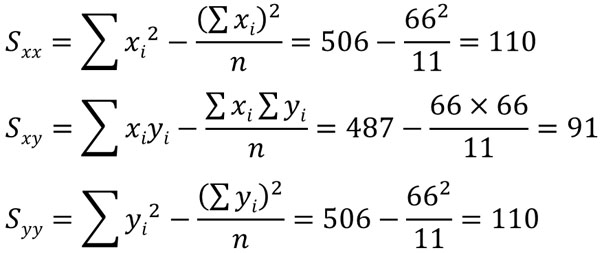
次に、以下の公式を利用して順位相関係数Rsを計算します。
- \(R_s=\displaystyle\frac{S_{xy}}{\sqrt{S_{xx}×S_{yy}}}\)
数字を代入すると、順位相関係数Rsは0.83になります。
\(R_s=\displaystyle\frac{91}{\sqrt{110×110}}≒0.83\)
こうして、計算方法1と同じ答えを得ることができました。
スピアマン検定表またはt分布表を利用して有意差を判断する
次に行うこととして、得られた順位相関係数Rsが有効かどうかを検定しましょう。すべてのデータについて、相関係数を計算することができます。ただ得られた相関係数について、意味のある相関係数かどうか判断できるようになりましょう。
そこで検定によって有意差を判断し、相関が有効かどうかを判断しましょう。なおスピアマンの順位相関係数では、サンプル数に応じて検定方法が異なります。
・サンプル数\(n\)が30以下の場合
標本のサンプル数が30以下の場合、スピアマン検定表を利用して判断しましょう。統計学の教科書にスピアマン検定表が掲載されているはずなので、有意水準0.05(または0.01)と比較するのです。
有意水準0.05となるRs値に比べて、計算したRs値が大きい場合、5%以下で起こる稀なイベントが生じていることになります。その場合は帰無仮説を棄却し、対立仮説を採用します。
・サンプル数\(n\)が30より多い場合
一方、サンプル数が30より多い場合はt分布を利用して判定しましょう。計算した順位相関係数Rsとサンプル数\(n\)を利用し、以下の公式に代入することで統計量Tを計算するといいです。
- \(T=r_s\sqrt{\displaystyle\frac{n-2}{1-(r_s)^2}}\)
スピアマンの順位相関係数では、統計量Tは自由度\(n-2\)のt分布に従います。そこで自由度を計算し、統計学の教科書に記載されているt分布表を確認しましょう。その後、有意水準とp値を比較することで相関があるかどうかを判定します。
相関関係があるかどうかを判断する
それでは、先ほどの例題について相関があるかどうかを判断しましょう。ここまで計算した結果をまとめると以下のようになります。
- サンプル数\(n\):11
- 順位相関係数Rs:0.83
サンプル数は30以下であるため、t分布ではなくスピアマン検定表を利用します。有意水準を0.05(5%)とすると、サンプル数11のとき、スピアマン検定表に記載されている数字は0.618です。
計算した順位相関係数Rsは0.83であるため、0.618よりも相関は強いです。つまり、5%以下で発生する稀なイベントが発生していると判断できます。そこで帰無仮説を棄却し、対立仮説を採用しましょう。つまり、広告費と売上に相関関係があると判断できます。
今回はスピアマン検定表を利用しましたが、サンプル数が多い場合はt分布を利用して判定します。この場合、先ほど解説した公式や自由度を利用し、t分布表を活用して有意水準とp値を比較しましょう。
スピアマンの順位相関係数を利用し、相関関係を確認する
ピアソンの相関係数はパラメトリック法であり、線形の関係があるかどうかを確認することができます。一方でノンパラメトリック法であり、\(x\)と\(y\)が連動して変化するかどうかを確認できるのがスピアマンの順位相関係数です。
線形かどうかに関係なく利用できるため、スピアマンの順位相関係数では曲線のグラフであっても問題ありません。また外れ値が含まれていても利用可能です。
なお順位相関係数Rsを得た後、有意差を判断しましょう。相関があるかどうかについて、検定することによって確かめるのです。検定するときは2つの方法があるため、最適な方法を選択しましょう。
ノンパラメトリック法により、順番を利用して相関関係を確認するのがスピアマンの順位相関係数です。スピアマンの順位相関係数を利用する場合、特徴や概念、計算方法を理解しましょう。






