図形の問題で重要な概念が三角比です。三角比を習うことによって、辺の長さを計算することができます。また、角度がわかるようになります。
三角比を理解していない場合、数学の問題を解けないだけでなく、物理の問題を解くこともできません。多くの場面で利用されるのが三角比です。
それでは、三角比とは何なのでしょうか。三角比の基本を学ぶとき、どのような公式があるのでしょうか。また、なぜ三角比は重要なのでしょうか。
一つの角度と辺の長さがわかれば、三角比を利用することによって、直角三角形のすべての角度と辺の長さを計算することができます。そこで、どのようにして三角比を利用し、図形の辺の長さを計算すればいいのか解説していきます。
三角比の定義:sin、cos、tanの覚え方
まず、三角比とは何でしょうか。この定義を理解しましょう。三角比では、必ず直角三角形を利用します。直角をもたない三角形では、三角比を利用することができません。
例えば、以下のような直角三角形があるとします。
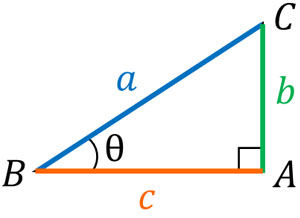
角度をθとするとき、sine(正弦:sin)・cosine(余弦:cos)・tangent(正接:tan)を以下のように表します。

θは角度であるため、θの値は異なります。θの角度が10°のときがあれば、70°のときもあります。いずれにしても、θは角度であると理解しましょう。このとき、直角三角形の斜辺とその他の辺の関係を表すのがsin、cos、tanです。
例えば、以下のときsinθ、cosθ、tanθの値は何でしょうか。

sin、cos、tanの定義を利用すると、以下のように値を得ることができます。
- \(sinθ=\displaystyle\frac{3}{5}\)
- \(cosθ=\displaystyle\frac{4}{5}\)
- \(tanθ=\displaystyle\frac{3}{4}\)
「一つの角度がわかっている直角三角形について、辺の長さの関係を表すのが三角比」と理解しましょう。
・sin、cos、tanの覚え方
なお、sin・cos・tanには覚え方があります。sinについて、sを筆記体を表すアルファベットを使います。またcosについて、cを利用しましょう。tanについてはtを使いましょう。そうすると、以下のようになります。
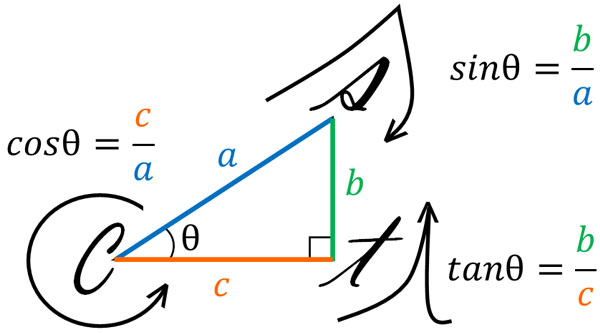
sin(正弦)については、sの筆記体を思い浮かべましょう。sの筆記体の書き順を理解して、\(a\)(斜辺)と\(b\)を分数で表します。sの筆記体を書くとき、斜辺\(a\)からスタートして、右の辺\(b\)に到着します。そのため、\(sinθ=\displaystyle\frac{b}{a}\)です。
cos(余弦)についても、cの書き順を思い浮かべましょう。cを書くとき、斜辺\(a\)からスタートして、下の辺\(c\)に到着します。そのため、\(cosθ=\displaystyle\frac{c}{a}\)です。
tan(正接)の覚え方も同じです。tを筆記体で書くとき、下の辺\(c\)からスタートして、右の辺\(b\)に到着します。そのため、\(tanθ=\displaystyle\frac{b}{c}\)です。
30°、45°、60°での三角比の値
なお、角度が違うとsinやcos、tanの値が変わります。ただ角度がわかれば、sinやcos、tanの値がわかります。三角比というのは、3つの辺の比を指します。角度が同じ場合、3つの辺の比は同じです。例えば、以下のように辺の長さが違っていたとしても、3つの辺の比は同じです。
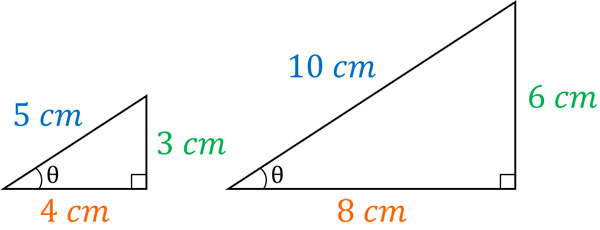
相似の図形では、辺の比が同じです。そのため、相似の図形ではsinθ、cosθ、tanθの値が同じになります。これが、角度がわかると三角比の値を決めることができる理由です。
ここまでの内容を理解した後、角度が30°や45°、60°のときの三角比を出せるようにしましょう。例えば角度が10°のとき、sin10°やcos10°の値は決まっているものの、これらの値を覚えている人はいません。一方で角度が30°や45°、60°の場合は例外的に三角比の値を出すことができます。
三平方の定理を学ぶとき、直角三角形の一つの角度が30°や45°になる場合、辺の比が以下のようになると教わっています。
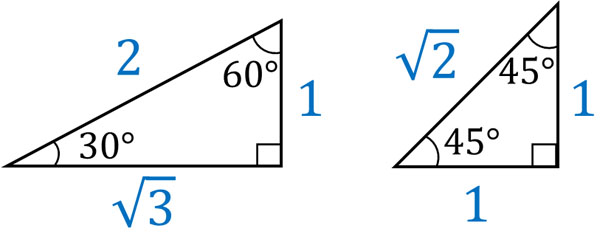
先ほど解説した通り、角度がわかれば三角比の値は一定です。このとき、角度が30°や45°、60°の場合に三角比は以下のようになります。
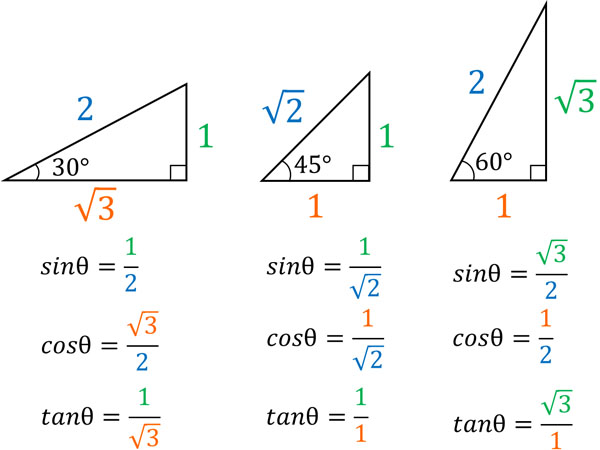
三角比の値を覚える必要はありません。つまり、例えばsin60°やtan45°の値を覚えるのは意味がないです。その代わり、図を描きましょう。角度が30°や45°、60°となる直角三角形を描くのです。その後、sinやcos、tanの値を出すのが正しいやり方です。
なぜ三角比を学ぶのが重要なのか
それでは、なぜ私たちは三角比を学ぶのでしょうか。この理由として、一つの角度と一つの辺の長さがわかれば、すべての角度と辺の長さを計算することができるからです。
例えば、以下の直角三角形で\(b\)の長さは何でしょうか。
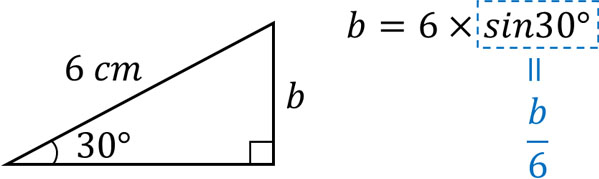
sin30°の値は同じです。直角三角形によって辺の長さは違うものの、辺の比は同じなのです。このとき、sin30°では分母が斜辺の長さになり、分子が右の辺の長さになります。そのため、\(sin30°=\displaystyle\frac{b}{6}\)と表すことができます。
言い換えると、\(sin30°\)と斜辺の長さをかけると、\(b\)の長さを求めることができます。参考までに、斜辺の長さにsinθをかけると必ず直角三角形のたての長さを出すことができます。sinθの分母は斜辺の長さであるため、sinθに斜辺の長さをかけることで、分子にあるたての長さのみ残ります。
また先ほど説明した通り、\(sin30°=\displaystyle\frac{1}{2}\)です。そのため、\(b\)の長さは以下のように計算できます。
\(b=6×sin30°\)
\(b=6×\displaystyle\frac{1}{2}\)
\(b=3\)
このように、斜辺を利用することによってほかの辺の長さを計算することができます。
物理で頻繁に三角比が利用される理由として、角度を利用して辺の長さを求めることができるからです。例えば建築設計をするとき、三角比を利用すればたてや横の長さがわかります。また辺の長さがわかれば、三角形の面積を出すことができます。
三角比を学ぶ理由としては、単純に便利だからです。角度を利用することによって、知りたい辺の長さを求めることができるのです。
三角比の相互関係を表す公式
なおsinθやcosθ、tanθには相互関係を表す公式があります。より詳しくいうと、例えばsinθの値がわかる場合、cosθとtanθの値を得ることができます。三角比には以下の公式があります。
- \(sin^2θ+cos^2θ=1\)
- \(tanθ=\displaystyle\frac{sinθ}{cosθ}\)
- \(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)
この公式のうち、\(sin^2θ+cos^2θ=1\)と\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)は覚えるようにしましょう。一方、\(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)は覚えてもいいし、覚えなくてもいいです。公式を簡単に得ることができるからです。
\(sin^2θ+cos^2θ=1\)の公式
この公式が成り立つ理由を理解するため、以下の直角三角形を考えましょう。
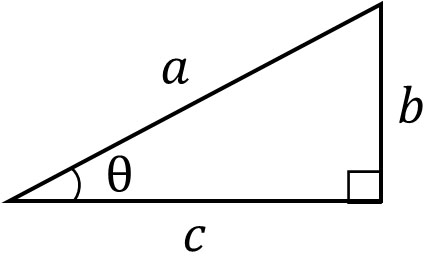
三平方の定理(ピタゴラスの定理)より、\(b^2+c^2=a^2\)です。また先ほど解説した方法によって、sinθがわかれば\(b\)の長さを計算できます。以下のようになります。
- \(b=a×sinθ\)
またcosθを利用すれば、\(c\)の長さを計算できます。\(cosθ=\displaystyle\frac{c}{a}\)であるため、cosθと\(a\)をかけると\(c\)を得ることができます。
- \(c=a×cosθ\)
そこで、\(b=a×sinθ\)と\(c=a×cosθ\)を\(b^2+c^2=a^2\)に代入しましょう。すると、以下のようになります。
\(b^2+c^2=a^2\)
代入すると
\(a^2×sin^2θ+a^2×cos^2θ=a^2\)
両辺を\(a^2\)でわる。
\(sin^2θ+cos^2θ=1\)
こうして、\(sin^2θ+cos^2θ=1\)の公式を証明することができます。
\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)の公式
なお、\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)については簡単に理解できると思います。以下の直角三角形について、\(sinθ=\displaystyle\frac{b}{a}\)です。また、\(cosθ=\displaystyle\frac{c}{a}\)です。

そのため、\(\displaystyle\frac{sinθ}{cosθ}\)は以下のようになります。

\(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)の公式
\(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)の公式については、\(sin^2θ+cos^2θ=1\)と\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)を利用することによって得ることができます。まず、\(sin^2θ+cos^2θ=1\)の両辺を\(cos^2θ\)でわりましょう。
\(sin^2θ+cos^2θ=1\)
\(\displaystyle\frac{sin^2θ}{cos^2θ}+1=\displaystyle\frac{1}{cos^2θ}\)
先に説明した通り、\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)です。つまり\(tan^2θ=\displaystyle\frac{sin^2θ}{cos^2θ}\)となります。そこで、この式を代入しましょう。
\(\color{red}{\displaystyle\frac{sin^2θ}{cos^2θ}}+1=\displaystyle\frac{1}{cos^2θ}\)
代入すると
\(tan^2θ+1=\displaystyle\frac{1}{cos^2θ}\)
こうして、\(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)の公式を得ることができます。\(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)は簡単な計算によって得ることができるため、前述の通りこの公式を覚えてもいいし、覚えなくてもいいです。
三角比の公式を利用し、ほかの三角比を得る
先ほどの公式を利用すれば、一つの三角比を得ることによって、ほかの三角比を求めることができます。
sinθまたはcosθがわかっている場合、\(sin^2θ+cos^2θ=1\)を利用することによってsinθ(またはcosθ)の値を出すことができます。その後、\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)を利用することでtanθの値を得られいます。
一方でtanθがわかっている場合はどうでしょうか。この場合、\(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)を利用することによってcosθの値を出すことができます。その後、\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)を利用することでsinθの値が得られます。
sinθ(またはcosθ)を利用し、三角比を求める
それでは、実際に計算してみましょう。sinθ(またはcosθ)がわかっている場合、公式を利用することによってほかの三角比を出せます。例えば、以下はどのような答えになるでしょうか。
- \(sinθ=\displaystyle\frac{2}{3}\)のとき、cosθとtanθの値は?(ただし、sinθ、cosθ、tanθはすべて正の値)
\(sin^2θ+cos^2θ=1\)より、以下のようにcosθの値を出すことができます。
\(\left(\displaystyle\frac{2}{3}\right)^2+cos^2θ=1\)
\(\displaystyle\frac{4}{9}+cos^2θ=1\)
\(cos^2θ=1-\displaystyle\frac{4}{9}\)
\(cos^2θ=\displaystyle\frac{5}{9}\)
cosθ>0のため、
\(cosθ=\displaystyle\frac{\sqrt{5}}{3}\)
こうして、\(cosθ=\displaystyle\frac{\sqrt{5}}{3}\)とわかります。また\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)を利用することによってtanθを出しましょう。以下のようになります。
\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)
\(tanθ=sinθ÷cosθ\)
\(tanθ=\displaystyle\frac{2}{3}÷\displaystyle\frac{\sqrt{5}}{3}\)
\(tanθ=\displaystyle\frac{2}{3}×\displaystyle\frac{3}{\sqrt{5}}\)
\(tanθ=\displaystyle\frac{2}{\sqrt{5}}\)
このように、sinθを利用してcosθとtanθの値を出せます。
tanθを利用し、sinθとcosθを得る
一方でtanθがわかっている場合、\(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)を利用しましょう。例えば、以下の答えは何でしょうか。
- \(tanθ=3\)のとき、sinθとcosθの値は?(ただし、sinθ、cosθ、tanθはすべて正の値)
\(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)に\(tanθ=3\)を代入しましょう。以下のようになります。
\(1+3^2=\displaystyle\frac{1}{cos^2θ}\)
\(10=\displaystyle\frac{1}{cos^2θ}\)
\(cos^2θ=\displaystyle\frac{1}{10}\)
cosθ>0のため、
\(cosθ=\displaystyle\frac{1}{\sqrt{10}}\)
次に\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)を利用してsinθの値を出しましょう。以下のようになります。
\(tanθ=\displaystyle\frac{sinθ}{cosθ}\)
\(tanθ×cosθ=sinθ\)
\(3×\displaystyle\frac{1}{\sqrt{10}}=sinθ\)
\(sinθ=\displaystyle\frac{3}{\sqrt{10}}\)
このように、公式を利用することによってすべての三角比を計算できます。
三角比の概念を理解し、sinθ・cosθ・tanθを計算する
図形を学ぶとき、最も重要な概念の一つが三角比です。三角比を利用することによって、すべての辺の長さと角度がわかります。三角比は非常に便利なため、建築や機械工学、電気、情報技術など、多くの物理分野で利用されています。
三角比で最も基本となるのがsine(正弦:sin)・cosine(余弦:cos)・tangent(正接:tan)です。sinやcos、tanが何を意味するのか理解しましょう。
また一つの角度がわかれば、sinθやcosθ、tanθの値もわかりますが、値を覚える必要はありません。ただ例外として角度が30°や45°、60°の場合では、すべての人がsinθやcosθ、tanθの値を計算によって得ることができます。
三角比を利用すれば、その他の辺の長さや角度がわかり、結果として高さや面積を計算することもできます。図形の計算や物理で頻繁に三角比が利用されるため、三角比の基本となる概念を理解しておきましょう。






