数学で直線上の点を考えるとき、最も重要な要素が距離です。2つの点を利用すれば、線分の距離を求めることができます。また、距離以外に重要な概念が内分点と外分点です。公式を利用することにより、内分点と外分点を計算できるようになりましょう。
なお点は直線上ではなく、平面上に存在することも多いです。そこで、平面上で2点間の距離を出せるようになりましょう。三平方の定理を利用すれば、2点間の距離を得ることができます。また公式を利用することにより、内分点と外分点を出すこともできます。
それに加えて、三角形の重心や対称な点を得られるようになりましょう。重心の計算では公式を利用します。対称な点では、2つの点を足して2で割れば対称な点の座標を計算できます。
直線上の点と平面上の点について、明確な座標を計算できるようになる必要があります。そこで、どのように公式を利用して計算すればいいのか解説していきます。
もくじ
直線上の線分の内分点と外分点:座標と公式
線分の長さを計算するのは容易です。点\(a\)と点\(b\)の距離は\(|b-a|\)です。点\(a\)と点\(b\)について、どちらの値が大きいのかわかりません。そこで、絶対値を加えることで必ず正の値に変換します。
それでは、内分点はどのように計算すればいいのでしょうか。線分を内側で分ける点を内分点といいます。例えば点Oが原点であり、OAの長さが3のとき、OAを1:2に内分する点Bはどこにあるでしょうか。点BがOAを1:2に内分する場合、以下のようになります。
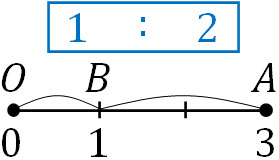
こうして、点Bの座標がわかります。\(OB:BA=1:2\)となっています。
一方でOAの長さが3のとき、OAを1:2に外分する点Bはどこにあるでしょうか。点BがOAを1:2に外分する場合、以下のようになります。

この場合であっても、\(OB:BA=1:2\)です。ただ先ほどとは異なり、点Bは線分OAの外側にあります。こうした点が外分点です。
・内分点と外分点の公式
なお実際には、原点Oを利用せず、2つの点(点Aと点B)を内分する点を求めることが多いです。点Aの座標を\(a\)、点Bの座標を\(b\)、線分ABの内分点を点P(座標\(x\))とすると、以下の図を作ることができます。
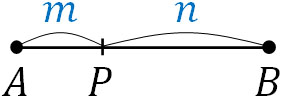
点Pが線分ABを\(m:n\)に内分する場合、以下のように計算できます。
\(AP:PB=x-a:b-x=m:n\)
\(n(x-a)=m(b-x)\)
\(x(n+m)=na+mb\)
\(x=\displaystyle\frac{na+mb}{m+n}\)
こうして、線分を内分する公式を得ることができました。なお、線分ABを\(m:n\)に外分する点Pを得る公式は以下になります。
- \(x=\displaystyle\frac{-na+mb}{m-n}\)

外分点Pの座標を計算するとき、\(m:(-n)\)に内分すると考えましょう。そのため内分点を得る公式を変形することにより、外分点を得る公式を作ることができます。
平面上の線分の内分点と外分点
なお内分点と外分点を計算するとき、直線上に点が存在するのではなく、平面上に点が存在するケースがひんぱんにあります。その場合、\(x\)軸と\(y\)軸に分けて内分点(または外分点)を計算しましょう。
例えば、点A\((x_a,y_a)\)と点B\((x_b,y_b)\)を\(m:n\)に内分する点Pの座標は以下のようになります。
- \(x\)座標:\(\displaystyle\frac{nx_a+mx_b}{m+n}\)
- \(y\)座標:\(\displaystyle\frac{ny_a+my_b}{m+n}\)
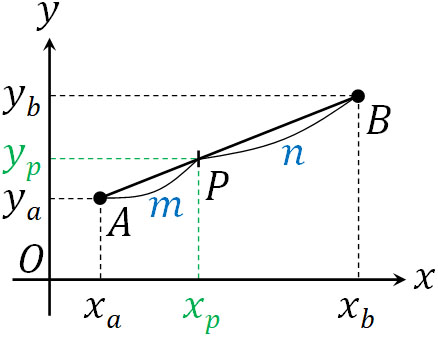
また、外分点Pの座標は以下のようになります。
- \(x\)座標:\(\displaystyle\frac{-nx_a+mx_b}{m-n}\)
- \(y\)座標:\(\displaystyle\frac{-ny_a+my_b}{m-n}\)
\(x\)軸と\(y\)軸をそれぞれ分けて計算することを理解すれば、平面上の線分に対する内分点と外分点を計算することができます。
平面上の2点間の距離
それでは、平面上の2点間の距離はどのように計算すればいいのでしょうか。計算方法は簡単であり、三平方の定理を利用しましょう。
平面上の点A\((x_a,y_a)\)と点B\((x_b,y_b)\)について、距離を計算しましょう。三平方の定理を利用すると、以下のように計算できます。
- \(AB=\sqrt{(x_b-x_a)^2+(y_b-y_a)^2}\)
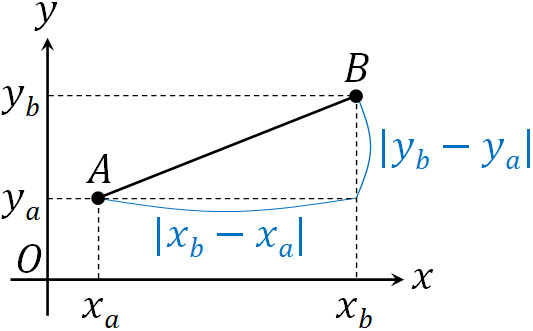
既に知っている事実であるため、この公式は何も問題なく理解できると思います。それでは、以下の問題の答えは何でしょうか。
- 点A\((1,2)\)と点B\((4,-1)\)から等距離にある\(x\)軸上の点Pの座標を求めましょう。
\(x\)軸上の点Pの座標を\((x,0)\)としましょう。\(AP=BP\)なので、以下の式を作ることができます。
\(AP^2=BP^2\)
\((1-x)^2+2^2=(4-x)^2+(-1)^2\)
\(x^2-2x+5=x^2-8x+17\)
\(6x=12\)
\(x=2\)
こうして、点Pの座標は\((2,0)\)とわかりました。
三角形の重心と公式
平面上の点でほかに重要な公式として、三角形の重心を求める公式があります。以下の△ABCについて、3辺AB、BC、CAの中点とそれぞれの頂点を結ぶ場合、交わる点Gを重心といいます。
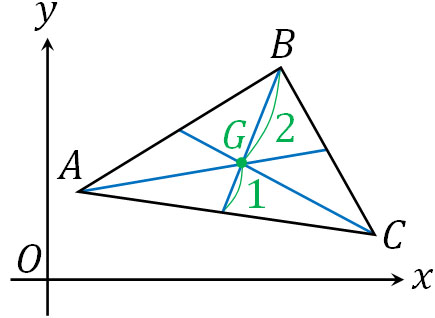
重心Gは「頂点と中点を結ぶ線を2:1で内分する点」です。
それでは、重心Gの座標はどのように計算すればいいのでしょうか。頂点の座標をA\((x_a,y_a)\)、B\((x_b,y_b)\)、C\((x_c,y_c)\)とすると、重心Gの座標は以下のようになります。
- \(x\)座標:\(\displaystyle\frac{x_a+x_b+x_c}{3}\)
- \(y\)座標:\(\displaystyle\frac{y_a+y_b+y_c}{3}\)
三角形の重心を得る公式は覚えてしまいましょう。
座標を利用して証明する
それでは、座標を利用することで証明問題を解いてみましょう。△ABCの重心をGとするとき、以下が成り立つことを証明しましょう。
- \(AB^2+BC^2+CA^2\)\(=3(GA^2+GB^2+GC^2)\)
座標を利用することで証明しましょう。どの場所を原点Oに設定してもいいですが、計算を楽にするため、\(x\)軸と\(y\)軸で0となる箇所が多くなるように原点Oを設定しましょう。そこで、以下のようにABの中点を原点Oにします。
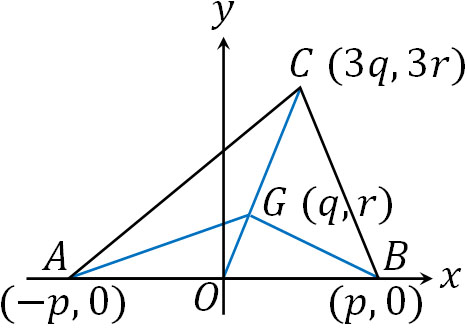
ここまで解説した内容を利用すると、それぞれの座標を以下のように表すことができます。
- A\((-p,0)\)
- B\((p,0)\)
- C\((3q,3r)\)
- G\((q,r)\)
原点OはABの中点であるため、点Aの座標を\((-p,0)\)とすると、点Bの座標は\((p,0)\)です。また重心Gの座標を\((q,r)\)とすると、点GはCOを2:1に内分するため、点Cの座標は\((3q,3r)\)となります。そこで、以下のように計算しましょう。
\(AB^2+BC^2+CA^2\)
\(=4p^2+(3q-p)^2+9r^2+(3q+p)^2\)\(+9r^2\)
\(=4p^2+(9q^2-6qp+p^2)\)\(+(9q^2+6qp+p^2)\)\(+18r^2\)
\(=6p^2+18q^2+18r^2\)
次に、以下の計算をしましょう。
\(3(GA^2+GB^2+GC^2)\)
\(=3(q+p)^2+3r^2+3(q-p)^2+3r^2\)\(+12q^2\)\(+12r^2\)
\(=3(q^2+2qp+p^2)\)\(+3(q^2-2qp+p^2)\)\(+12q^2\)\(+18r^2\)
\(=6p^2+18q^2+18r^2\)
こうして同じ式を作ることができたため、\(AB^2+BC^2+CA^2\)\(=3(GA^2+GB^2+GC^2)\)が成り立つと証明できました。
点に対して対称な点の求め方
平面上の点では、特定の点に対して対称な点を求めなければいけないこともあります。例えば点A\((1,2)\)を基準にするとき、\((4,5)\)と対称な点はどこでしょうか。
対称な点を\((x,y)\)としましょう。点Aを基準に対称というのは、点Aが\((4,5)\)と\((x,y)\)の中点であることを意味しています。そのため\(x\)軸に着目すると、以下の式を作ることができます。
\(1=\displaystyle\frac{4+x}{2}\)
\(x=-2\)
また\(y\)軸に着目すると、以下の式を作ることができます。
\(2=\displaystyle\frac{5+y}{2}\)
\(y=-1\)
こうして、対称な点の座標は\((-2,-1)\)とわかります。
特定の点に対して対称な点を求めるというのは、中点の性質を利用して計算するのと意味が同じです。そのため点A\((a,b)\)に対して、2点P\((x_p,y_p)\)とQ\((x_q,y_q)\)が対称のとき、以下の関係が成り立ちます。
- \(a=\displaystyle\frac{x_p+x_q}{2}\)
- \(b=\displaystyle\frac{y_p+y_q}{2}\)
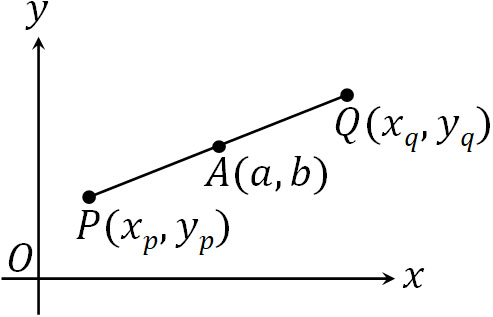
点に対して対称な点を計算するとき、中点の性質を利用しましょう。
直線上の点と平面上の点での座標を計算する
特定の点を計算できるようになることは重要です。例えば測量をしたり、建物図形の計算をしたりするとき、座標を求められるようにならなければいけません。
そこで直線上の点と平面上の点について、座標を計算できるようになりましょう。線の長さを計算したり、内分点・外分点を得たりするのです。内分点と外分点を計算するとき、公式を利用しましょう。
なお平面上の点を学ぶとき、三角形の重心を計算できるようになる必要があります。頂点と中点を結ぶとき、2:1に内分する点が重心です。また、重心の位置を計算するときは公式を利用しましょう。
図形において、点の座標を計算するのは最も基本的な内容の一つです。そこで公式を利用して、座標を得られるようになりましょう。






