三角方程式の解き方：不等式や置き換え、公式の利用法

三角関数を含む方程式を三角方程式といいます。式にsinθやcosθ、tanθを含むとき、弧度法を利用して値や角度を計算できるようになりましょう。このとき、不等式を含む問題が出されることもあります。

三角方程式では複数の解が存在するケースがひんぱんにあります。また不等式を含む方程式では、図を描かないと不正解になりやすいです。

また置き換えや公式を利用することによって三角方程式を解かなければいけないことも多いです。この場合、三角方程式を含む問題であっても、二次方程式や判別式など、その他の分野で学ぶ数学の知識を利用することになります。

それでは、どのように考えて三角方程式を解けばいいのでしょうか。三角方程式の計算方法を解説していきます。

三角方程式の解：sinθ、cosθ、tanθ

度数法を利用して三角比の問題を解くことができる場合、弧度法を利用する三角方程式についても問題を解くことができます。

三角方程式を解くとき、必ず図形を利用しましょう。図を利用しない場合、高確率で計算ミスをします。それでは$0≦θ<2π$のとき、以下の方程式の答えは何でしょうか。

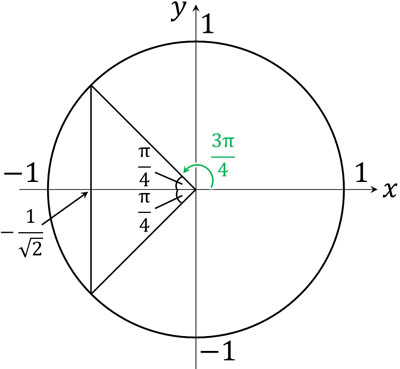
• $cosθ=-\displaystyle\frac{1}{\sqrt{2}}$

図を作ると、以下のように$\displaystyle\frac{3π}{4}$（135°）と$\displaystyle\frac{5π}{4}$（225°）で$cosθ=-\displaystyle\frac{1}{\sqrt{2}}$になるとわかります。

それでは$0≦θ<2π$のとき、以下の問題の答えは何でしょうか。

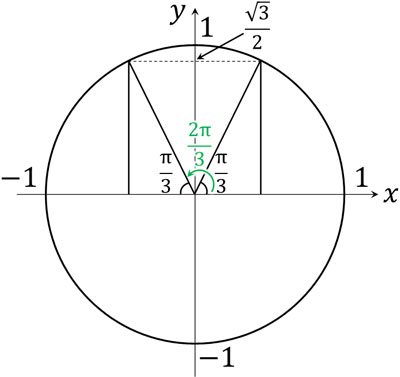
• $sinθ=\displaystyle\frac{\sqrt{3}}{2}$

先ほどと同様に図を作ると、$\displaystyle\frac{π}{3}$（60°）と$\displaystyle\frac{2π}{3}$（120°）で$sinθ=\displaystyle\frac{\sqrt{3}}{2}$になるとわかります。

図を利用することにより、最も基本的な三角方程式を解けるようになります。

三角不等式と不等式での範囲

次に、三角関数に不等式が利用されている場合の問題を解きましょう。三角不等式を解くときには、まず三角方程式を解きましょう。その後、図を利用することによって不等式を満たすθの範囲を確認するのです。

それでは$0≦θ<2π$のとき、以下の問題の答えは何でしょうか。

• $sinθ<-\displaystyle\frac{1}{2}$

まず、$sinθ=-\displaystyle\frac{1}{2}$を解くと$θ=\displaystyle\frac{7}{6}π,\displaystyle\frac{11}{6}π$となります。そこで$-\displaystyle\frac{1}{2}$よりも値が小さくなる$sinθ$の角度を確認しましょう。

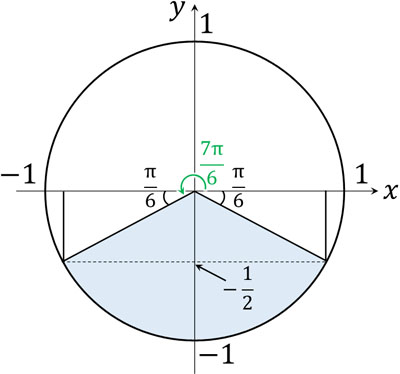
そうすると、$\displaystyle\frac{7}{6}π<θ<\displaystyle\frac{11}{6}π$が答えとわかります。次に、$0≦θ<2π$のとき、以下の問題を解いてみましょう。

• $tanθ≧\displaystyle\frac{1}{\sqrt{3}}$

$tanθ=\displaystyle\frac{1}{\sqrt{3}}$を満たすθの値は$θ=\displaystyle\frac{π}{6},\displaystyle\frac{7π}{6}$です。そこで図を作り、答えを確認しましょう。

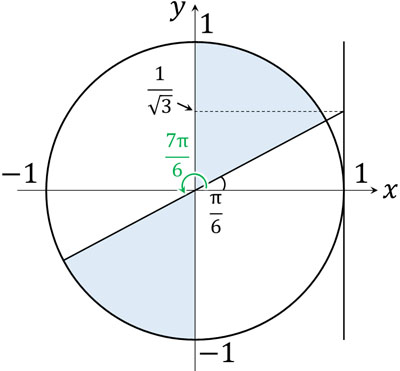
こうして、$\displaystyle\frac{π}{6}≦θ<\displaystyle\frac{π}{2}$、$\displaystyle\frac{7π}{6}≦θ<\displaystyle\frac{3π}{2}$が答えであるとわかりました。なおtanθでは、$θ≠\displaystyle\frac{π}{2},\displaystyle\frac{3π}{2}$であることに注意しましょう。

置き換えを用いて三角方程式、不等式を解く

それでは、少し複雑な三角方程式を解いてみましょう。三角方程式を解くとき、最も一般的な方法として置き換えがあります。特定の変数を$t$などの文字に置き換えることにより、答えを得るのです。それでは$0≦θ<2π$のとき、以下の答えは何でしょうか。

• $\sqrt{2}cos\left(θ+\displaystyle\frac{π}{3}\right)=1$

$\sqrt{2}cos\left(θ+\displaystyle\frac{π}{3}\right)=1$は$cos\left(θ+\displaystyle\frac{π}{3}\right)=\displaystyle\frac{1}{\sqrt{2}}$です。それでは、θがどのような値のときに$\displaystyle\frac{1}{\sqrt{2}}$になるのでしょうか。

$θ+\displaystyle\frac{π}{3}=t$としましょう。そうすると、式は$cost=\displaystyle\frac{1}{\sqrt{2}}$になります。この式を解くと、$t=\displaystyle\frac{π}{4},\displaystyle\frac{7π}{4}$です。

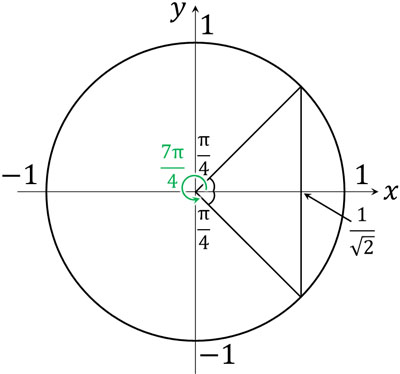
なお$θ+\displaystyle\frac{π}{3}=t$であるため、$t=\displaystyle\frac{π}{4},\displaystyle\frac{7π}{4}$に代入しましょう。つまり、以下の式を解きます。

• $θ+\displaystyle\frac{π}{3}=\displaystyle\frac{π}{4}$
• $θ+\displaystyle\frac{π}{3}=\displaystyle\frac{7π}{4}$

これらの式を解くと、$θ=-\displaystyle\frac{π}{12},\displaystyle\frac{17π}{12}$となります。なお$0≦θ<2π$であるため、$-\displaystyle\frac{π}{12}$の代わりに$\displaystyle\frac{23π}{12}$を利用しましょう。そのため、答えは$θ=\displaystyle\frac{17π}{12},\displaystyle\frac{23π}{12}$です。

公式を用いて三角方程式を変形する

次に、公式を利用することで解くことのできる問題を確認しましょう。sinθやcosθ、tanθを含む問題では、以下の公式を利用することで一種類の三角関数で表すようにしましょう。

• $sin^2θ+cos^2θ=1$
• $tanθ=\displaystyle\frac{sinθ}{cosθ}$
• $1+tan^2θ=\displaystyle\frac{1}{cos^2θ}$

それに加えて、置き換えを利用することによって二次方程式や三次方程式の問題に変形できます。それでは$0≦θ<2π$のとき、以下の問題の答えは何でしょうか。

• $2cos^2θ+sinθ-1=0$

$sin^2θ+cos^2θ=1$であるため、以下のように式を変形しましょう。

$2cos^2θ+sinθ-1=0$

$2(1-sin^2θ)+sinθ-1=0$

$2sin^2θ-sinθ-1=0$

$sinθ=t$としましょう。そうすると、$2t^2-t-1=0$となります。そこで、この式を解きます。

$2t^2-t-1=0$

$(2t+1)(t-1)=0$

$t=-\displaystyle\frac{1}{2},1$

sinθが$-\displaystyle\frac{1}{2},1$となるとき、$θ=\displaystyle\frac{π}{2},\displaystyle\frac{7π}{6},\displaystyle\frac{11π}{6}$です。こうして、答えを得ることができました。

三角関数の最大値と最小値

三角関数が関わる計算では、最大値と最小値を求めなければいけないこともあります。このとき、三角関数が含まれているものの、二次方程式や三次方程式の問題を解くときと考え方は同じです。それでは$0≦θ<2π$のとき、以下の問題の答えは何でしょうか。

• $y=2cos^2θ+sinθ-1$の最大値と最小値を求めましょう。

先ほど解説した通り、$sin^2θ+cos^2θ=1$を利用し、$sinθ=t$とすると式は$y=2t^2-t-1$となります。そこで、この式を以下のように変形しましょう。

$y=2t^2-t-1$

$y=2\left(t^2-\displaystyle\frac{t}{2}\right)-1$

$y=2\left(t-\displaystyle\frac{1}{4}\right)^2-\displaystyle\frac{9}{8}$

こうして、軸が$t=\displaystyle\frac{1}{4}$となる二次関数であるとわかります。なお、$-1≦sinθ≦1$です。そのため、$-1≦t≦1$の範囲で最大値と最小値を確認しましょう。

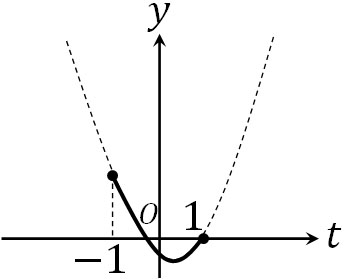
図より、最小値は頂点となるため、$t=sinθ=\displaystyle\frac{1}{4}$のとき、$y=-\displaystyle\frac{9}{8}$が最小値です。また$t=sinθ=-1$のとき、$y=2$が最大値になります。こうして、最大値と最小値を計算することができました。

三角方程式の解の存在範囲を計算する

三角関数の性質を利用するものの、先ほどの問題のように、三角方程式の問題は一般的な数学の計算と同じです。それでは、次は以下の問題を解いてみましょう。

• $cos^2θ+2αsinθ-α-1=0$を満たすθが存在するとき、定数$α$の値の範囲を求めましょう。

公式を利用し、以下のように式を変形しましょう。

$cos^2θ+2αsinθ-α-1=0$

$(1-sin^2θ)+2αsinθ-α-1=0$

$sin^2θ-2αsinθ+α=0$

$sinθ=t$とすると、$t^2-2αt+α=0$となります。$-1≦sinθ≦1$であるため、$-1≦t≦1$です。つまり、$-1≦t≦1$の範囲に少なくとも一つの解をもつことができればいいです。そこで、以下のように場合分けをしましょう。

① $-1≦t≦1$に2つの実数解をもつ（重解を含む）

2つの実数解（または重解）をもつ場合、以下の条件をすべて満たせばいいです。

• 判別式：$D≧0$
• $f(1)≧0$
• $f(-1)≧0$

・判別式：$D≧0$の計算

$4α^2-4α≧0$

$α(α-1)≧0$

$α≦0,1≦α$

・$f(1)≧0$の計算

$1-2α+α≧0$

$α≦1$

・$f(-1)≧0$の計算

$1+2α+α≧0$

$α≧-\displaystyle\frac{1}{3}$

3つの条件を満たす範囲は$-\displaystyle\frac{1}{3}≦α≦0$、$α=1$です。

② $-1≦t≦1$に一つの実数解があり、その他の場所に一つの実数解がある

$-1≦t≦1$の範囲に二つの実数解があるのではなく、「$-1≦t≦1$の範囲に一つの実数解があり、その他の場所にもう一つの実数解をもつケース」を考えましょう。$-1≦t≦1$の範囲に一つの実数解があれば、$cos^2θ+2αsinθ-α-1=0$を満たすθが存在することになります。

この条件を満たす式は以下になります。

• $f(1)×f(-1)≦0$

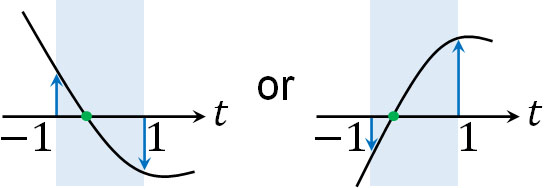
そこで、以下の計算をしましょう。

$f(1)×f(-1)≦0$

$(1-α)(1+3α)≦0$

$(α-1)(3α+1)≧0$

$α≦-\displaystyle\frac{1}{3},1≦α$

そこで①と②の条件を組み合わせると、$α≦0,1≦α$が正解とわかります。

三角関数を用いる方程式を解く

三角関数を解くとき、弧度法を用いて角度を計算できるようになりましょう。また、三角不等式を解けることも重要です。これらは図を用いて答えを得ましょう。

なお三角方程式によっては、置き換えをすると計算しやすくなるケースがあります。そこで、$t$などの文字を利用して置き換えをしましょう。場合によっては、公式を利用することで式を整理しなければいけないこともあります。

応用問題では三角関数の性質を活用し、ほかの分野の数学知識も用いて問題を解くことになります。二次方程式や三次方程式の性質を利用して答えを得るようにしましょう。

三角関数が関わる式では問題の解き方があります。そこで、どのようにsinθやcosθ、tanθの性質を活用すればいいのか理解しましょう。