指数と対数は親せきであり、指数を対数へ変換できます。また指数関数が存在するため、対数関数も存在します。そこで、対数関数のグラフや計算方法を学びましょう。
なお、対数には条件があります。どのような数字であっても底や真数になれるわけではないのです。そのため対数関数では、底や真数の値が取り得る範囲を確認しなければいけません。
対数の性質を理解したら、対数方程式や対数不等式に関する問題を解けるようになりましょう。このとき、真数条件に注意する必要があります。また対数関数を利用し、最大値と最小値を計算しましょう。置き換えを利用することにより、二次関数や三次関数のグラフを得て計算するのです。
それでは、どのように考えて対数関数に関する問題を解けばいいのでしょうか。対数の性質を利用して、対数関数を解けるようになりましょう。
もくじ
対数関数のグラフと形
指数を対数へ変換するとき、グラフの形が変化します。指数関数と対数関数でどのようにグラフが変わるのか確認しましょう。
指数関数\(y=a^x\)のグラフに対して、\(y=x\)のグラフを基準に対称移動させると\(y=log_ax\)のグラフになります。以下が指数関数と対数関数のグラフです。
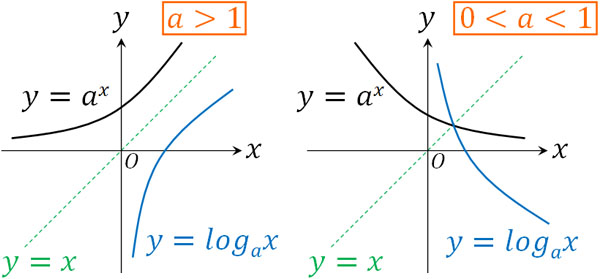
なお指数関数では、\(a>1\)なのか、それとも\(0<a<1\)なのかによってグラフの形が変化します。そのため対数関数でも同様に、底の値によってグラフの形が変化します。
底の条件と真数条件
指数の計算では、\(M=a^x\)とするとき\(a>0\)という条件があります。底\(a\)がマイナスの値だと、\(x\)の値によって答えがプラスになったり、マイナスになったりを繰り返します。これを防ぐため、\(a>0\)とするのです。
また\(a=1\)の場合、指数関数では常に答えが1です。そのため計算する意味がなく、指数関数では\(a≠1\)となります。つまり、\(a>0\)かつ\(a≠1\)です。
指数と対数はほぼ同じ数式であるため、底の条件は対数にも適用されます。つまり対数を利用するとき、底の条件は\(a>0\)かつ\(a≠1\)です。
また\(a>0\)であるため、指数の計算をするとき必ず\(M>0\)になります。そのため対数を利用するとき、真数\(M\)の値は必ず\(M>0\)になります。これを真数条件といいます。対数関数では真数条件を利用して範囲を求めることが多いため、必ず理解しなければいけない概念です。
対数方程式の計算:真数条件の利用
それでは、実際に対数に関する問題を解いてみましょう。対数方程式の計算では、得られた答えのうち、どちらか一方のみが答えであるケースは多いです。これは、底の条件や真数条件を満たす必要があるからです。
例題として以下の問題を解きましょう。
- \(log_2x+log_2(x-2)=3\)
計算すると以下のようになります。
\(log_2x+log_2(x-2)=3\)
\(log_2x(x-2)=3log_22\)
\(log_2x(x-2)=log_22^3\)
\(log_2x(x-2)=log_28\)
\(x(x-2)=8\)
\(x^2-2x-8=0\)
\((x-4)(x+2)=0\)
\(x=-2,4\)
ただ、答えは\(x=-2,4\)ではありません。理由としては、真数条件を考慮していないからです。問題の式を確認すると、\(log_2x+log_2(x-2)=3\)です。そのため真数条件より、以下の2つの条件を満たす必要があります。
- \(x>0\)
- \(x-2>0\)
2つの条件を同時に満たすためには、\(x>2\)である必要があります。また\(x=-2\)と\(x=4\)について、真数条件を満たすのは\(x=4\)です。そのため、答えは\(x=4\)です。
置き換えにより、対数方程式を解く
次に、置き換えを利用することによって対数方程式を解きましょう。指数関数の計算では置き換えをひんぱんに利用します。これは、対数関数でも同様です。特に対数を利用して二乗や三乗の計算をする場合、置き換えによって問題を解きましょう。
それでは、以下の問題の答えは何でしょうか。
- \(log_x2=log_2x^2+1\)
まず、底の条件と真数条件を確認しましょう。
\(log_x2\)を確認すると、底の条件より\(x>0\)かつ\(x≠1\)です。また\(log_2x^2\)を確認すると、真数条件より\(x^2>0\)、つまり\(x≠0\)です。対数方程式の答えを得るとき、この2つの条件を満たす必要があります。それでは、以下のように計算しましょう。
\(log_x2=log_2x^2+1\)
\(\displaystyle\frac{log_22}{log_2x}=2log_2x+1\)
\(\displaystyle\frac{1}{log_2x}=2log_2x+1\)
次に、\(t=log_2x\)と考えて置き換えましょう。
\(\displaystyle\frac{1}{t}=2t+1\)
\(1=2t^2+t\)
\(2t^2+t-1=0\)
\((2t-1)(t+1)=0\)
\(t=-1,\displaystyle\frac{1}{2}\)
そこで、\(log_2x=-1\)と\(log_2x=\displaystyle\frac{1}{2}\)を解きましょう。
・\(log_2x=-1\)の計算
\(log_2x=-1\)
\(log_2x=-1log_22\)
\(log_2x=log_22^{-1}\)
\(log_2x=log_2\displaystyle\frac{1}{2}\)
\(x=\displaystyle\frac{1}{2}\)
・\(log_2x=\displaystyle\frac{1}{2}\)の計算
\(log_2x=\displaystyle\frac{1}{2}\)
\(log_2x=\displaystyle\frac{1}{2}log_22\)
\(log_2x=log_22^{\frac{1}{2}}\)
\(log_2x=log_2\sqrt{2}\)
\(x=\sqrt{2}\)
こうして、\(x=\displaystyle\frac{1}{2},\sqrt{2}\)になるとわかります。なお、\(x=\displaystyle\frac{1}{2},\sqrt{2}\)は底の条件と真数条件を満たします。そのため、答えは\(x=\displaystyle\frac{1}{2},\sqrt{2}\)です。
対数不等式と真数条件の利用
真数条件がより重要になるのが対数不等式です。対数不等式の範囲を計算するとき、真数条件を利用する必要があります。
なお対数不等式では、底\(a\)の値に注意しましょう。指数不等式では、\(a>1\)なのか、それとも\(0<a<1\)なのかによって大小関係が変化します。これは対数不等式でも同様であり、以下のように不等式の向きが変化します。
- \(a>1\)の場合:\(log_aA>log_aB\)なら、\(A>B\)
- \(0<a<1\)の場合:\(log_aA>log_aB\)なら、\(A<B\)
グラフを確認すれば、なぜこの関係になるのかわかります。
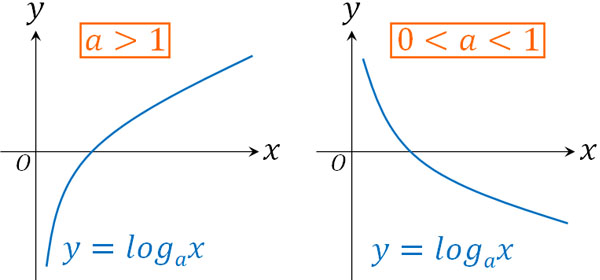
\(0<a<1\)の場合、\(x\)の値が大きくなるほど、\(y\)の値は小さくなります。そのため、\(0<a<1\)の場合は大小関係が反対になります。この性質を理解して対数不等式の問題を解かなければいけません。
また対数不等式の問題を解くとき、必ず以下の2つを確認しましょう。
- 底が異なる場合、公式を利用して底をそろえる
- 真数条件(\(M>0\))と底の条件(\(a>0,a≠1\))を確認する
対数不等式に限らず、対数が関わるほかの計算でも必須となる手順ではありますが、必ずこれらの作業を行いましょう。それでは、以下の問題の答えは何でしょうか。
- \(log_22x<log_327\)
底が異なるため、同じ底にしましょう。以下のように式を変形します。
\(log_22x<log_327\)
\(log_22x<log_33^3\)
\(log_22x<3\)
\(log_22x<3log_22\)
\(log_22x<log_28\)
底は2であり、1より大きいため、対数を外すときに不等号の大小関係は同じです。不等号の向きは同じになるため、不等号を外すときは以下のようになります。
\(2x<8\)
\(x<4\)
底をそろえることにより、\(x<4\)を得ることができました。それでは、真数条件と底の条件を確認しましょう。
問題の式を確認すると、底の条件は満たしています。また真数条件より、\(2x>0\)です。つまり、\(x>0\)です。そこで真数条件と合わせて、\(0<x<4\)が答えとわかりました。
対数関数での最大値と最小値
指数関数の計算で置き換えを利用したのと同じように、対数関数でも置き換えを利用することによって計算することができます。置き換えによって二次関数や三次関数を計算できるのです。
以下の例題を利用して、対数関数での最大値と最小値を計算してみましょう。
- \(\displaystyle\frac{1}{4}≦x≦2\)のとき、\(y=(log_24x)(log_2x)\)について最大値と最小値を計算しましょう。
以下のように計算します。
\(y=(log_24x)(log_2x)\)
\(y=(log_24+log_2x)(log_2x)\)
\(y=(log_22^2+log_2x)(log_2x)\)
\(y=(2+log_2x)(log_2x)\)
ここで、\(log_2x=t\)としましょう。これにより、以下のように二次方程式の計算が可能です。
\(y=(2+t)t\)
\(y=t^2+2t\)
\(y=(t+1)^2-1\)
こうして、\(t=-1\)を軸とする二次方程式とわかります。なお問題文より、\(x\)の範囲は\(\displaystyle\frac{1}{4}≦x≦2\)であり、これは真数条件を満たしています。また\(log_2x=t\)であるため、\(t\)の範囲は以下のようになります。
\(\displaystyle\frac{1}{4}≦x≦2\)
\(log_2\displaystyle\frac{1}{4}≦log_2x≦log_22\)
\(-2≦t≦1\)
底は2であるため、対数を外すときに不等号の向きは変わりません。また\(t\)の範囲と二次方程式のグラフを確認すると、最大値と最小値を得ることができます。
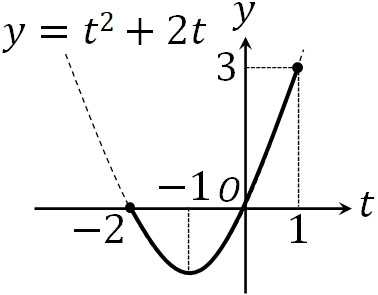
図より、\(t=-1\)のとき、つまり\(x=2^{-1}=\displaystyle\frac{1}{2}\)のとき、最小値-1になります。また\(t=1\)のとき、つまり\(x=2\)のとき、最大値3となります。こうして、置き換えを利用することによって答えを得ることができました。
対数関数に関する問題の解き方を学ぶ
対数を利用して計算することは多く、指数関数に対する対数関数のグラフの形を学びましょう。また対数関数の計算では、真数条件と底の条件をひんぱんに利用します。計算するとき、真数条件と底の条件を満たす必要があるのです。
そこで、対数の性質を利用して対数方程式や対数不等式を解けるようになりましょう。このとき、底が\(a>1\)なのか、それとも\(0<a<1\)なのかによって、対数を外すときに不等式の向きが異なることに注意しましょう。
これらの内容を理解すれば、置き換えを利用することによって対数関数の最大値と最小値を得られるようになります。置き換えをした後、二次方程式や三次方程式を計算しましょう。
真数条件や底の条件など、対数に特有の条件があります。これらを認識して、対数関数の問題を解きましょう。






