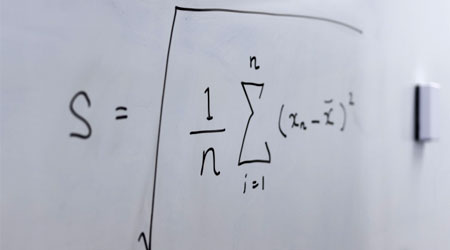統計学で最も重要であり、すべての人が学ぶ概念として正規分布(ガウス分布)があります。データが正規分布でない場合、統計処理できないケースは多いです。正規分布でない場合はデータの取り方に誤りがあり、データ収集をやり直さなければいけないこともあります。
データが正規分布になっていることは非常に重要です。そのため統計学を学ぶとき、正規分布が何を意味しているのか理解するようにしましょう。
正規分布を利用すれば、発生確率がどれくらいになるのか判断できます。また正規分布を理解することにより、なぜ統計学で標準偏差が頻繁に利用されるのかわかります。
正規分布について学ぶとき、その詳細を理解している人は少ないです。そこで難しい公式なしに、正規分布がもつ意味を解説していきます。
もくじ
正規分布(ガウス分布)ではヒストグラムの形が重要になる
統計学での正規分布(ガウス分布)とは、要は「山のような形になっているデータ」と理解しましょう。以下のようなデータが正規分布です。
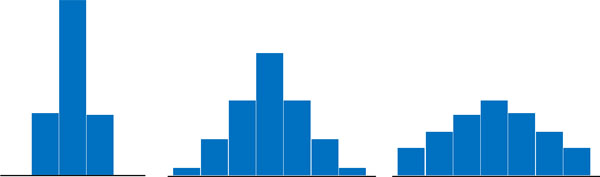
統計データを得るとき、正規分布になるケースがほとんどです。場合によっては正規分布にならないケースはあるものの、ほとんどのケースで正規分布になるというわけです。
例えば以下のようなデータを取るとき、正規分布になります。
- 全国模試の点数分布
- 国民の男性の身長分布
- コインを何度も投げ、表が出た回数の合計
統計データによって、縦長の正規分布なのか、それとも横長の正規分布なのかは異なります。いずれにしても、山のような形になる場合は正規分布というわけです。
一方、山のような形でない場合、正規分布ではありません。以下のように判断します。
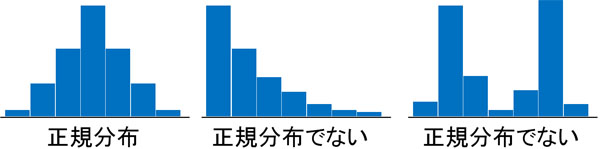
正規分布なのかそうでないのかは、グラフの形を見れば容易に判断できます。
正規分布していないデータは統計処理が難しい
それでは、なぜ正規分布(ガウス分布)しているかどうかが重要なのでしょうか。この理由として、正規分布していないデータは統計処理が難しいからです。
通常のデータであれば、ピークが一つあり、左右対称のグラフになります。ただピークが二つあったり、左右対称でなかったりするグラフの場合、ほとんどのケースで「何かしらの原因により、データの取得方法に誤りがある」といえます。
例えば身長の分布を調べるとき、以下のようなグラフになる場合、明らかに変であるとわかります。
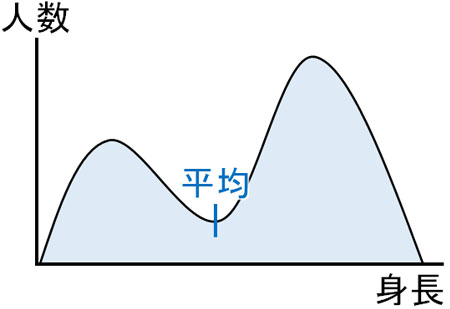
またこのデータの平均値(Average)や中央値(Median)を確認すると、平均値や中央値はグラフの中央に現われます。ただこのグラフはピークが二つあるため、平均値を得ることができても、「平均値として利用できない」ということは直感的にわかると思います。
統計データを取るとき、例えば「小学生の身長」と「20歳以上の大人の身長」のデータを組み合わせると、先ほどのデータが完成されます。ただこの場合、データの取り方がダメなので統計データの取得をやり直さなければいけません。
正規分布でない場合、何かしらの異常値が入っており、統計処理しても正しい結果を得られない場合がほとんどです。また統計データの解析では、正規分布していることが前提となっているケースが多いです。
このようなさまざまな理由により、正規分布していない場合は「統計データの集め方が間違っていないか」を確認しなければいけません。
正規分布(ガウス分布)の近似と4つの性質
なお前述の通り、ヒストグラムが山のような形になっている場合、正規分布となります。ただヒストグラムでは縦長の棒を利用したグラフであるため、曲線ではありません。そこでヒストグラムについて、正規分布(確率分布)となるよう、以下のように近似します。
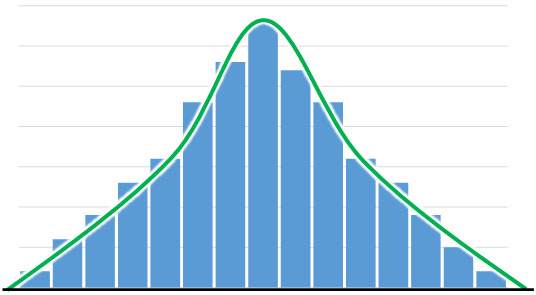
棒グラフのデータを正規分布へ近似することによって、曲線のカーブに変換することができます。参考までに、統計データを正規分布へ近似するための式として以下があります。
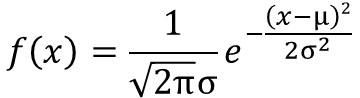
ただ、この公式を覚える必要はありません。ほとんどの人は意味を理解できないと思うので、むしろこの公式を忘れてしまって問題ないです。重要なのは、「公式を利用することで正規分布へ近似し、曲線のカーブを得ることができる」ことを理解しましょう。
それでは、正規分布にはどのような性質があるのでしょうか。正規分布には以下の4つの性質があることを理解しましょう。
- 1つのピークが表れる
- グラフの形は左右対称
- 端へ行くとゼロに近づく
- 面積は必ず1になる
「1つのピークが表れる」「グラフの形は左右対称」「端へ行くとゼロに近づく」については、特に問題なく理解できるはずです。正規分布は英語でNormal Distributionとなり、よくある一般的な分布のことを指します。通常、統計データを集めると正規分布になります。
また面積が必ず1になる理由としては、正規分布は確率分布だからです。例えば全国模試の分布を調べるとき、模試を受けたすべての人を足すと100%(1)になります。確率分布であるため、すべての正規分布では面積が1になります。
なお数学では、面積を計算するときに積分を利用します。そのため「正規分布の面積が1になる」ことを難しい数式で表すと以下のようになります。
- \(\displaystyle \int_{α}^{β} f(x) dx=1\)
ただ、この公式についても意味は難しくなく、先ほど説明した通り、「正規分布のすべての面積を足すと1になる」ことを表しています。統計学を学ぶとき、難しい公式が出されることはあるものの、意味を理解すれば内容は難しくありません。
連続型確率分布(確率密度関数)での確率:離散型確率分布との違い
ここまでの内容を理解したうえで、「正規分布が何を意味しているのか」について、より詳細に学びましょう。正規分布で利用するグラフというのは、別名で連続型確率分布(確率密度関数)と呼ばれます。
確率の計算をするときの確率変数には、主に2種類あります。以下のようになります。
- 離散型確率変数:コインやサイコロなど、決まった値を出せる
- 連続型確率変数:身長や体重など、小数点以下の値を出せる
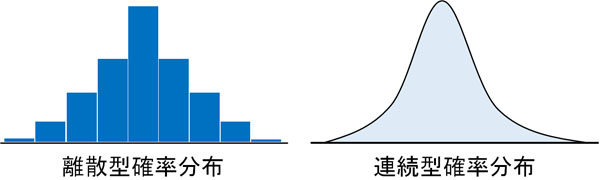
例えばサイコロを投げるとき、目の数は1や2、3など明確に決まった数字になります。つまり数字と数字に間があり、統計データを取るときは連続していない値になります。デコボコしたデータになる場合は離散型確率変数と呼び、このデータを利用することによって離散型確率分布のグラフとなります。
一方で連続型確率変数はどのようなデータになるのでしょうか。例えば体重を測定するとき、64kgピッタリということはなく、実際には64.38kgなどのように小数点を利用して表すことができます。場合によっては、より小さい値を利用することによって表記することも可能です。
そのためデータはデコボコしておらず、一つの曲線のように連続したデータとなります。こうした統計データを連続型確率変数といいます。
正規分布については、先ほど解説した通りヒストグラムを曲線へと近似します。たとえ元データが離散型確率分布に従っていたとしても、連続型確率分布として曲線のデータとみなします。そのため「正規分布では、連続型確率分布を調べる」と考えましょう。
また連続型確率分布の場合、離散型確率分布とは異なり、特定の確率関数を定義することができません。データは連続しているため、特定の値の確率を出すことができないのです。
そこで離散型確率変数について、特定区間の面積(積分値)を計算することによって確率を定義するのが確率密度関数です。確率密度関数とは、「特定の範囲について、どれくらいの確率で起こるのかを表す関数」と理解しましょう。
確率密度関数では、面積を計算することによって確率を得ることができます。正規分布ではすべての面積を足すと1になるため、確率密度関数を利用することによって確率を計算できるというわけです。
要は、正規分布は曲線のグラフであるため、「連続したデータを利用する連続型確率分布(確率密度関数)で考える」と理解すればいいです。
正規分布と標準偏差の関係性
次に正規分布(ガウス分布)と標準偏差の関係を学びましょう。なぜ統計学で標準偏差を頻繁に利用するかというと、正規分布のグラフを描くとき、平均値からどれだけズレているのか容易に判断できるからです。
グラフが正規分布に従う場合、標準偏差を利用することによって以下のようにデータが分布します。
- 平均値から「標準偏差×1」の範囲:データ全体の68.3%
- 平均値から「標準偏差×2」の範囲:データ全体の95.5%
- 平均値から「標準偏差×3」の範囲:データ全体の99.7%
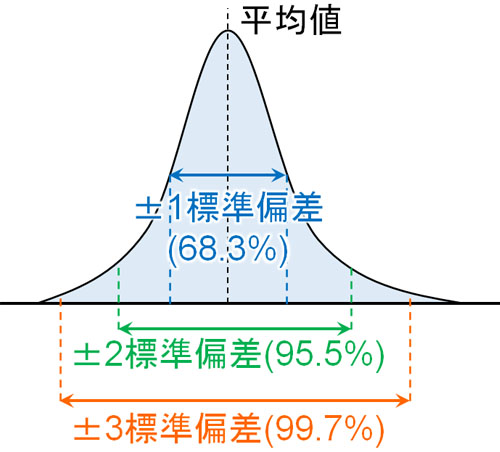
例えば全国模試のテストを受け、標準偏差の2倍以上の得点を取っていることがわかった場合、圧倒的に優れた点数を取っていることがわかります。トップ4.5%に入っているからです。平均値と標準偏差を利用することによって、データがどれだけ平均値からズレているのか判断できるのです。
また統計学では平均値を\(μ\)(ミュー)、標準偏差を\(σ\)(シグマ)と表します。そのため正規分布について、\(μ\)と\(σ\)を利用して表すと以下のようになります。
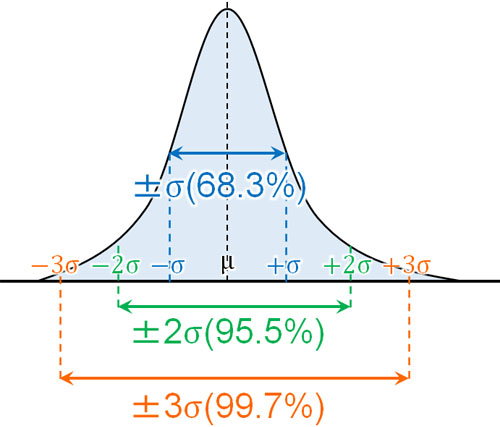
統計学を学ぶとき、記号を利用して記されることが頻繁にあります。そこで\(μ\)や\(σ\)を利用しているグラフを提示されたとき、何を意味しているのか理解できるようにしましょう。
確率変数の変換により、正規分布を標準正規分布に変換する
ただ統計データによって正規分布(ガウス分布)の形が異なります。当然ながら、標準偏差の値も違います。そこですべての正規分布について、横軸を同じにしましょう。つまりグラフの形について、伸び縮みさせたり、平行移動させたりするのです。
まず、グラフを平行移動させましょう。具体的には、平均値の部分を0にします。確率変数\(X\)(元データ)について、平均値\(μ\)を引けば、平行移動によって平均値だった部分は0になります。
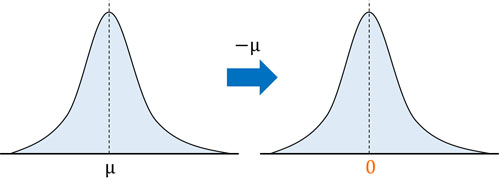
次にグラフの横軸の長さを変えましょう。具体的には、確率変数\(X\)(元データ)について標準偏差\(σ\)で割ります。\(σ\)で割るため、元の正規分布について、\(σ\)だった値は1になります。また、\(2σ\)だった場所は2になります。
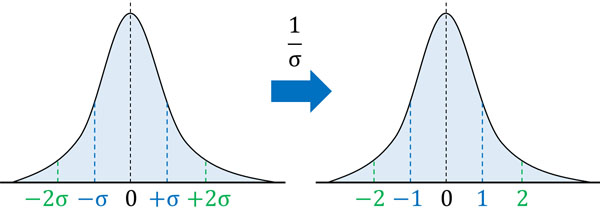
こうして確率変数\(X\)に対して平均値\(μ\)を引き、標準偏差\(σ\)で割ることによって、「真ん中がゼロ、標準偏差の幅が1のグラフ」を描くことができます。このような分布を標準正規分布といいます。
標準偏差\(σ\)で割るため、どのようなグラフであったとしても、中心は0であり、標準偏差の幅は1になります。そのため標準正規分布へ変換することによって、すべての正規分布について確率を計算しやすくなります。
なお確率変数\(X\)(元データ)に対して平均値\(μ\)を引き、標準偏差\(σ\)で割るとき、新たに得られる確率変数\(Z\)(標準正規分布で利用できるデータ)は以下の式によって表されます。
- \(Z=\displaystyle\frac{X-μ}{σ}\)
統計学で正規分布を学ぶとき、必ずこの式が出てきます。この式を暗記しても意味がなく、公式が何を意味しているのか理解しましょう。
ここまでの話を理解すれば、確率変数\(X\)に対して平均値\(μ\)を引く必要があるため、\(μ\)を利用して引き算をすればいいとわかります。また標準偏差\(σ\)で割ることによって、中心と標準偏差の幅を1に変換します。こうして得られる新たな確率変数\(Z\)が標準正規分布で利用可能なデータとなります。
確率変数と標準正規分布表から確率を求める
それでは確率変数と標準正規分布を利用することによって、実際に確率を求めてみましょう。標準正規分布に変換することによって、すべてのデータについて標準正規分布表を利用できるようになります。
標準正規分布を利用すると何が便利かというと、以下の面積を調べることによって発生する確率を得ることができるからです。
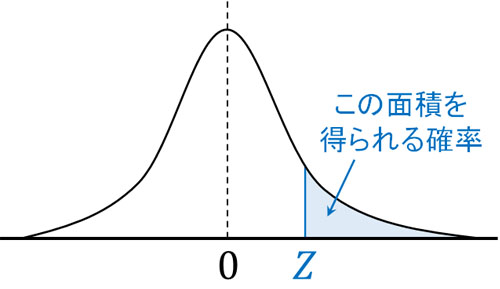
標準正規分布表には、さまざまな確率変数\(Z\)に対する面積がまとめられています。このとき、\(Z\)値よりも大きい値(または小さい値)が発生する確率を求めることができます(\(Z\)値での確率ではないことに注意しましょう)。
・標準正規分布表を利用し、確率を計算する
それでは、実際に標準正規分布表を利用して確率を求めてみましょう。例えば、以下の問題の答えは何でしょうか。
- Aさんのテストの点数は80点でした。平均点が55点、標準偏差が15の場合、Aさんは上位何パーセントでしょうか。
まず確率変数\(X\)を標準化しましょう。Aさんのテストの点数\(X\)は80です。そのため平均点55を引き、標準偏差15で割ることによって、新たな確率変数\(Z\)を得ることができます。
\(Z=\displaystyle\frac{80-55}{15}≒1.67\)
こうして、標準正規分布で利用できる確率変数として1.67を得ることができました。次に、標準正規分布表を確認しましょう。前述の通り、標準正規分布表では「あらゆるデータに対応する面積と確率の値」が既に計算されています。一部を記すと、以下が標準正規分布表になります。
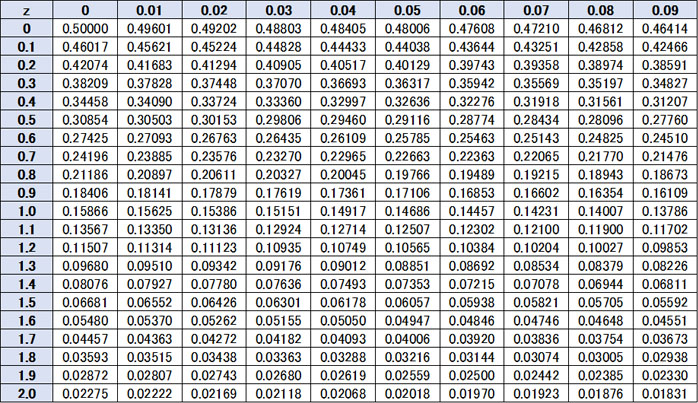
要は、「この標準正規分布表を利用して確率を出す」と理解すればいいです。
先ほど、Aさんが取ったテストの点数80点について、確率変数\(Z\)が1.67であると計算しました。そこで以下のように、1.67に対応する部分を確認しましょう。
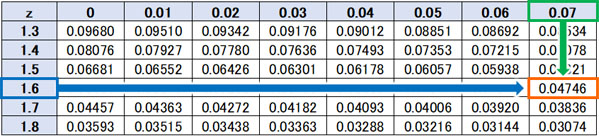
標準正規分布表を確認すると、確率変数\(Z\)が1.67のとき、起こる確率は0.04746(約4.7%)であるとわかります。つまり、Aさんはトップ4.7%の優れた成績であるとわかります。
なぜ標準正規分布へ変換するかというと、標準正規分布表を利用できるようになるからです。確率変数\(Z\)を得た後、標準正規分布表を利用すれば、特定の事象が起こる確率を調べることができます。
\(Z\)値がマイナスのときも標準正規分布表の考え方は同じ
なお確率変数\(Z\)がマイナスになることもあります。平均値よりも値が低い場合、標準正規分布を利用するときの確率変数\(Z\)はマイナスになるのです。
この場合も考え方は確率変数\(Z\)がプラスのときと同じであり、標準正規分布表を利用することによって、以下の部分の面積を出しましょう。
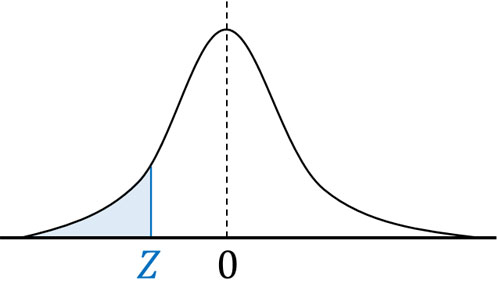
例えば、以下の問題の答えは何でしょうか。
- Bさんのテストの点数は40点でした。平均点が50点、標準偏差が15の場合、Bさんは上位何パーセントでしょうか。
先ほどと同じように、確率変数\(Z\)を計算しましょう。
\(Z=\displaystyle\frac{40-50}{15}≒-0.67\)
こうして、確率変数\(Z\)が-0.67とわかりました。なお正規分布は左右対称です。そのため-0.67というのは、0.67と意味が同じです。そこで以下のように、標準正規分布表を利用して確率を出しましょう。
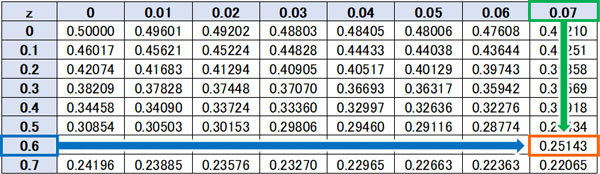
こうして、確率変数\(Z\)が0.67のとき、起こる確率は0.25143(約25.1%)とわかります。つまり、Bさんは下位25.1%にいます。
また上位何パーセントにいるかを計算するためには、100%から引けばいいです。\(100-25.1=74.9\)なので、Bさんは上位74.9%にいるとわかります。
正規分布について、左右両方の面積が含まれるかどうかを確認する
なお場合によっては、標準正規分布の左右両方の面積が含まれているケースがあります。この場合、問題文に注意しましょう。
例えば、以下の問題の答えは何でしょうか。
- 1歳6か月の子供の体重を測定するとき、平均値が10kg、標準偏差が1kgとします。子供の体重に異常が疑われる10%の親に通知を送る場合、どの範囲の体重が正常でしょうか。
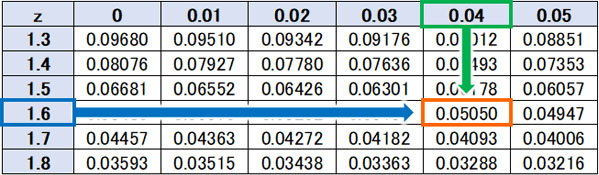
体重が異常というのは、体重が重いケースと軽いケースの2パターンあります。つまり上位5%と下位5%に含まれている子供について、体重に異常があると判断します。正規分布について左右の面積が含まれた状態で10%となるため、標準正規分布表では片方の面積が5%(0.05)となる部分を調べるようにしましょう。
そうすると確率変数\(Z\)が1.64のとき、片方の面積が約5%になるとわかります。
そのため、正常と判断される体重の範囲は以下のようになります。
\(±1.64=\displaystyle\frac{X-10}{1}\)
\(X=10±1.64\)
こうして8.36~11.64kgの体重の場合は正常であり、そうでない場合は異常な体重と判断します。いずれにしても、正規分布の左右の面積が含まれているかどうかを確認しなければいけないケースがあることを理解しましょう。
統計学で重要な正規分布を学ぶ
統計学を学ぶとき、最も重要な要素であり、すべての人が学ぶ内容に正規分布(ガウス分布)があります。ただ実際のところ、正規分布が何を意味しているのか理解している人は少ないです。
特殊な公式を利用し、ヒストグラムを近似することによって正規分布を得ることができます。このとき正規分布は連続型確率分布(確率密度関数)であるため、曲線のグラフを描きます。
また正規分布に対して平均値\(μ\)を引き、標準偏差\(σ\)で割ることによって、標準正規分布で利用できる確率変数\(Z\)を得ることができます。この値を利用することによって、いくらの確率で特定の値を得られるのか計算できます。
正規分布を利用することによって、多くの統計処理が可能になります。そこで、こうした正規分布(ガウス分布)の基本を理解しましょう。