統計学では同時確率分布と周辺確率分布を学びます。概念は難しくないものの、それぞれの言葉が何を意味しているのか理解する必要があります。
なお同時確率分布と周辺確率分布を理解するとき、事前に離散型確率分布と連続型確率分布を学ぶ必要があります。離散型確率分布のケースにおいて同時確率分布と周辺確率分布を学べば、内容を理解しやすいです。その後、2変数の連続型確率分布を学びましょう。
なお同時確率分布や周辺確率分布では、同時に独立性を学ぶことが多いです。そこで、確率の独立性と独立同一分布の概念を理解しましょう。
確率分布には種類があります。また、確率分布はそれぞれ異なる性質をもちます。そこで統計学を学ぶとき、確率分布の特徴を理解しましょう。
もくじ
確率分布には離散型確率分布と連続型確率分布がある
まず、確率分布には大きく2つの種類があります。確率分布には離散型確率分布と連続型確率分布があるのです。違いとしては以下のように考えましょう。
- 離散型確率分布:デコボコしている確率分布
- 連続型確率分布:なめらかな曲線の確率分布
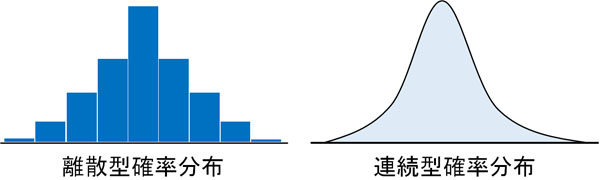
なぜ、このような違いを生じるのでしょうか。
グラフに確率を記すとき、決まった値を出せる場合は離散型確率分布となります。例えばコインやサイコロの場合、特定の値を出すことができます。そのため確率をグラフに記すとき、必ずデコボコの形になります。
一方で体重や身長をグラフに記す場合はどうでしょうか。例えば体重の場合、60.00kgピッタリのケースは少なく、59.92kgや60.06kgであることはよくあります。また、より小さい単位を使えば、さらに細かく分けることができます。
そのため確率のグラフを作るとき、曲線のグラフになります。こうした曲線グラフを連続型確率分布といいます。
離散型確率分布での同時確率分布と周辺確率分布
同時確率分布と周辺確率分布を学ぶとき、離散型確率分布を利用して理解しましょう。連続型確率分布を利用する場合、概念が難しくなるからです。
例えば以下の場面を考えてみましょう。
- 袋X(白玉、青玉、赤玉が含まれる)から一つ玉を取り出した後、袋Y(黒玉、黄玉、緑玉が含まれる)から一つ玉を取り出す。
色玉を取り出す確率がそれぞれ以下のような場合、確率分布の表を作りましょう。

このとき、すべてのペアの確率を表すのが同時確率です。また、XまたはYのみの確率を抽出すると周辺確率になります。
つまり、以下の部分が同時確率分布と周辺確率分布になります。
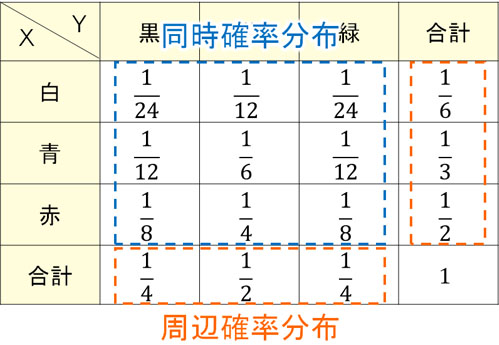
周辺確率分布では、特定の確率のみ表すことになります。Xの確率のみ、またはYの確率のみ表す場合、周辺確率分布となります。一方ですべての確率を表す場合、同時確率分布になります。
条件付き確率分布は同時確率分布の一部を表す
参考までに、確率分布には条件付き確率分布もあります。どのような確率分布になるのでしょうか。
条件付き確率分布とは、特定の条件のときに起こる確率を表します。先ほどの表であれば、例えば「袋Xから白玉を取り出すときの確率分布」となります。つまり、以下の部分が条件付き確率分布になります。
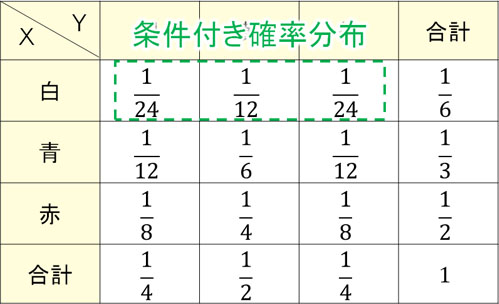
統計学の教科書を含め、多くの人は数式と共に同時確率分布や周辺確率分布、条件付き確率分布を学びます。ただ、数式を用いても理解するのは難しいです。そこで表を使えば、誰でも簡単に同時確率分布や周辺確率分布、条件付き確率分布を理解できるようになります。
- 同時確率分布:すべてのペアの確率分布
- 周辺確率分布:XまたはYの確率分布
- 条件付き確率分布:特定の条件下での確率分布
離散型確率分布での確率分布には、こうした種類が存在します。
2変数の連続型確率分布はどう考えるのか
ここまで、離散型確率分布を前提にして解説してきました。離散型確率分布の場合、起こる確率を明確な値で表すことができます。
一方で連続型確率分布の場合、特定の値を出すことができません。身長が170.00cmぴったりの人はほとんどおらず、例えば170.05cmなどのようになります。
この場合、特定の値ではなく範囲を利用します。例えば身長\(170cm≦X≦175cm\)、体重\(60kg≦Y≦65kg\)などのように範囲を規定します。その後、決めた範囲の面積を計算しましょう。
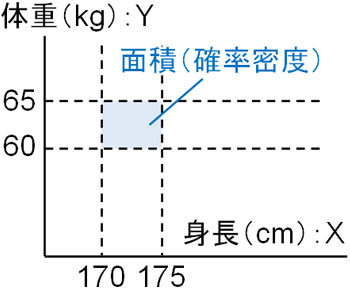
連続型確率分布では、範囲内の面積を確率として表します。これを確率密度といいます。要は、面積が確率を表すというわけです。
連続型確率分布では、同時密度関数\(h(x,y)\)と積分記号を利用し、以下のように表されます。
- \(\displaystyle \int_{-∞}^∞ \displaystyle \int_{-∞}^∞h(x,y) dxdy=1\)
ただ、おそらくこうした数式を見ても理解できないと思います。そこで、数式が何を意味しているのか学びましょう。
積分というのは面積を表します。また範囲内の面積をすべて足す場合、確率は1(100%)になります。そのため\(h(x,y)\)の面積をすべて足すと1なります。先ほどの数式には、こうした意味があります。
前述の通り、連続型確率分布では確率密度(範囲内の面積)を利用して確率を出します。そのため範囲内の面積を出す必要があります。これを数式で表すと、積分記号を利用することになるというわけです。
確率変数の独立性とは何か
なお同時確率分布や周辺確率分布を学ぶとき、独立性の検証についても同時に学ぶことが多いです。周辺確率の確率変数Xと確率変数Yについて、独立かどうか確認するのです。確率変数での独立とは、「一つの事象が起こっている場合であっても、ほかの事象に影響を与えないこと」を指します。
2つの事象が独立である場合、互いの確率に影響を及ぼすことはありません。そのため独立の場合、Aが起こる確率P(A)とBが起こる確率P(B)は以下の関係になります。
- \(P(A∩B)=P(A)×P(B)\)
なお、事象が3つや4つに増えたとしても考え方は同じです。例えば事象が3つの場合、独立な場合は以下の関係になります。
- \(P(A∩B∩C)=P(A)×P(B)×P(C)\)
独立かどうかの判定をするとき、考え方は難しくありません。例えばコインとサイコロを投げる場面を考えましょう。コインを投げた結果が表であっても裏であっても、サイコロの確率は変化しません。
例えば、「コインが表&サイコロの目が1になる場面」を考えてみましょう。コインを投げて表になる確率P(A)は\(\displaystyle\frac{1}{2}\)です。また、サイコロの目が1になる確率P(B)は\(\displaystyle\frac{1}{6}\)です。コインとサイコロは独立しているため、私たちはかけ算によって確率を計算します。
\(P(A∩B)=P(A)×P(B)\)\(=\displaystyle\frac{1}{2}×\displaystyle\frac{1}{6}\)\(=\displaystyle\frac{1}{12}\)
コインが表&サイコロの目が1になる確率\(P(A∩B)\)というのは、コインが表になる確率P(A)とサイコロの目が1になる確率P(B)を利用することで計算できます。
確率変数X(コイン)と確率変数Y(サイコロ)が独立な場合、互いに無関係です。そのため独立な場合、XとYの周辺確率をかけ算することによって同時確率を計算できます。
先ほど、袋Xと袋Yを利用して同時確率分布と周辺確率分布の表を提示しました。例えば袋Xから赤玉を取り出し、袋Yから緑玉を取り出すとします。このときXの周辺確率(赤玉を取り出す確率)とYの周辺確率(緑玉を取り出す確率)をかけることで、両方の条件を満たす同時確率を得ることができます。
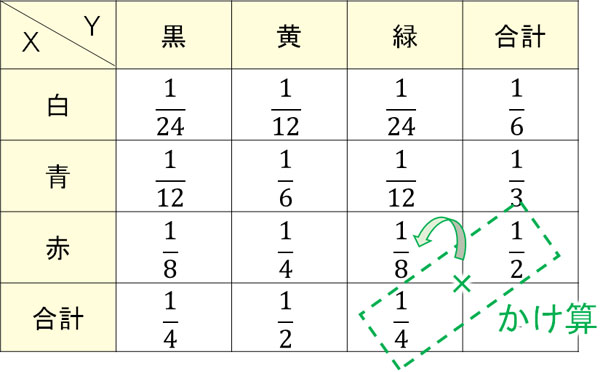
また、表を確認するとすべての同時確率について、周辺確率を利用して計算できることがわかります。
周辺確率というのは、確率変数Xまたは確率変数Yについて、特定の場面での確率を指します。また互いに独立の場合、かけ算をすることによって同時確率を計算できます。
コインとサイコロの例からわかる通り、独立性の意味は難しくありません。ただ同時確率分布や周辺確率分布を学ぶとき、難しい数式と共に独立性の説明をする教科書が多いです。
そこで難しく考えず、「独立な場合、Aが出る確率(Xの周辺確率)とBが出る確率(Yの周辺確率)のかけ算をすると、AとBを同時に得られる確率(同時確率)を得られる」と理解しましょう。
一方で独立でない場合だと、2つの周辺確率をかけても同時確率を得ることはできません。いずれにしても独立かどうかというのは、同時確率と周辺確率を確認することによって判断できます。
同じ確率分布で独立な場合、独立同一分布に従う
なお独立性について理解したら、次は独立同一分布を理解しましょう。離散型確率分布または連続型確率分布において、互いに独立で同じ確率分布の場合、「独立同一分布に従う」と判断します。
例えばサイコロを投げるとき、1回目の結果が何であったとしても、2回目の結果に影響を与えません。1回目の結果に関係なく、2回目に1の目がでる確率は\(\displaystyle\frac{1}{6}\)です。イカサマがない場合、確率分布に影響はありません。
このようにサイコロを投げるときには、以下の2つの性質があります。
- 独立性:互いに独立している
- 同一分布:確率分布(周辺確率)がどれも同じ(確率はすべて\(\displaystyle\frac{1}{6}\))
このように独立性と同一分布の両方を満たす場合、「確率変数は独立同一分布に従う」と表現します。
確率分布の理解は統計学で重要
統計学では必ず確率分布を学びます。確率分布には種類があり、最初に理解しなければいけないのが離散型確率分布と連続型確率分布です。これら2つの確率分布の性質は異なるため、どのように確率を計算するのか理解しましょう。
また離散型確率分布を学んだら、同時確率分布と周辺確率分布が何を意味しているのか理解しましょう。難しい概念ではないため、表を利用すれば誰でも簡単に内容を把握できます。なお連続型確率分布については、面積を用いて確率密度を計算します。
なお、同時確率分布や周辺確率分布を学ぶとき、同時に独立性や独立同一分布を習うことが多いです。そこで、確率の独立性や独立同一分布の意味を理解しましょう。
確率分布の種類や性質への理解は統計学を学ぶときに必須です。そこで、それぞれの確率分布が何を意味しているのか学びましょう。






