統計学では累積分布関数を学びます。確率を足すだけであるため、概念は非常に簡単です。難しい数式を利用する必要はなく、本来はシグマ\(Σ\)や積分を利用しなくても累積分布関数が何か理解できます。
なぜ累積分布関数を学ぶのが重要かというと、私たちの身の周りでひんぱんに利用されるからです。また、統計処理をすることで有意差の判定をするとき、累積分布関数が利用されます。二項検定やZ検定(標準正規分布を利用する検定)など、多くの場面で累積分布関数は重要です。
それでは、累積分布関数にはどのような意味があるのでしょうか。また、確率密度関数や正規分布との違いは何なのでしょうか。
累積分布関数は統計学で重要な概念であるものの、多くの教科書ではシグマや積分の記号を利用しているため理解しにくいです。そこで、こうした数学の記号を利用しなくても理解できるように解説していきます。
もくじ
確率を足すのが累積分布関数:離散型確率分布での例
統計を学ぶとき、最初に理解しなければいけないのが確率です。ただ、確率の計算については中学や高校で既に学んでいると思います。
累積分布関数を学ぶとき、離散型確率分布を利用しましょう。離散型確率分布とは、コインやサイコロのように、明確な確率を出せるケースを指します。
例えばコインを投げて表が出る確率は\(\displaystyle\frac{1}{2}\)であり、サイコロを投げて1の目が出る確率は\(\displaystyle\frac{1}{6}\)です。このように明確な確率の計算が可能な場合、離散型確率分布となります。要は、一般的な確率の計算と考えましょう。
それでは、コインを投げる場面を考えましょう。前述の通り、コインを投げて表が出る確率は\(\displaystyle\frac{1}{2}\)です。それでは、コインを3回投げて表が出る確率はいくらでしょうか。この場合、それぞれ以下のようになります。
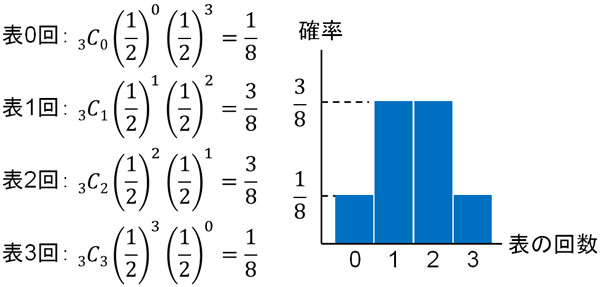
一方、累積分布関数では確率を足していきます。上に記した結果を利用すると、以下のようになります。

このように確率を計算する場合、累積分布関数を\(F(x)\)で表します。
計算方法は簡単であり、確率を足すだけ
このように考えると、累積分布関数は非常に概念が簡単であるとわかります。確率をすべて足すことによって確率を計算するだけです。
例えばサイコロを投げるとき、出る目の確率はすべて\(\displaystyle\frac{1}{6}\)です。そのため、一般的な確率分布と累積分布関数(確率分布の足し算)を比べると以下のようになります。
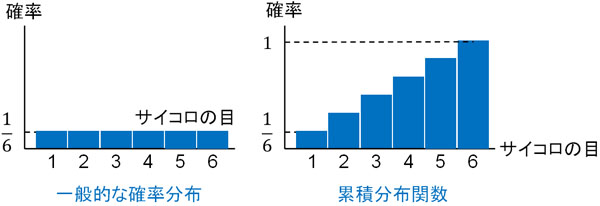
サイコロではすべての確率が\(\displaystyle\frac{1}{6}\)であるため、一般的な確率分布ではたて軸の値がすべて\(\displaystyle\frac{1}{6}\)になります。一方で累積分布関数では、すべての確率を足していきます。そのため、最終的に必ず確率は1になります。
例えば、以下のような確率変数Xと確率P(X)となる場合、累積分布関数はどのように計算すればいいでしょうか。
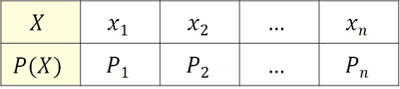
先ほど解説した通り、累積分布関数ではすべて足しましょう。累積分布関数を\(F(x)\)とすると、以下のようになります。
- \(F(x)=P_1+P_2+…+P_n\)
- \(F(x)=\displaystyle\sum{P(X)}\)
すべて足すことを数学ではシグマ\(Σ\)を利用して表します。要は、これまで説明した通り、すべての確率を足せばいいと理解すれば問題ありません。
例えばサイコロを投げるとき、2以下(サイコロの目が1または2)になる確率は何でしょうか。サイコロではすべての確率が\(\displaystyle\frac{1}{6}\)であるため、以下のようになります。
\(F(2)=\displaystyle\frac{1}{6}+\displaystyle\frac{1}{6}=\displaystyle\frac{1}{3}\)
一方、サイコロを投げて5以下になる確率は以下のようになります。
\(F(2)=\displaystyle\frac{1}{6}\)\(+\displaystyle\frac{1}{6}\)\(+\displaystyle\frac{1}{6}\)\(+\displaystyle\frac{1}{6}\)\(+\displaystyle\frac{1}{6}\)\(=\displaystyle\frac{5}{6}\)
統計学の教科書を利用して累積分布関数を学ぶとき、シグマを含む難しい数式が出てきます。ただ足し算であることを理解すれば、累積分布関数は特に難しい概念ではありません。
有意差の判定で確率の足し算がひんぱんに利用される
なお累積分布関数は統計学でひんぱんに利用されます。統計学を私たちが学ぶ理由として、有意差(差があるかどうか)を客観的に判断できるようにするためです。
例えばサイコロを6回投げ、1の目が4回出たとき、このサイコロには細工があるでしょうか。人によってはイカサマと考えるかもしれませんし、人によっては偶然と考えるかもしれません。ただ統計処理をすれば、差があるかどうか(イカサマがあるかどうか)を判断できます。
このとき利用するのが累積分布関数です。統計処理をするとき、特定の確率を計算することはありません。基準点よりも極端なケースを含めて確率を計算します。
例えば先ほどの例であれば、「サイコロを6回投げ、1の目が4回出る確率」で有意差を判断してはいけません。より極端な結果を含めて確率を合計するのです。つまり、以下の確率をすべて足します。
- サイコロを6回投げ、1の目が4回出る確率
- サイコロを6回投げ、1の目が5回出る確率
- サイコロを6回投げ、1の目が6回出る確率
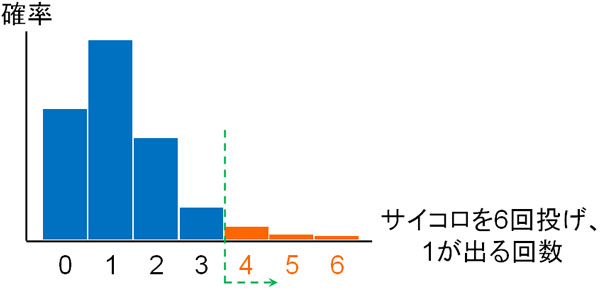
このように極端なケースを含めて確率を計算し、有意差(差があるかどうか)を判断するのが統計で重要になります。つまり累積分布関数というのは、統計学ですべての人が利用することになるのです。
参考までに、「サイコロを6回投げ、1の目が4回または5回、または6回出る確率」を合計すると約0.00866(0.87%)になります。
統計では0.05(5%)を基準とします。つまり基準となる確率(有意水準)を0.05とするとき、これよりも低い確率のイベントが起こっているのであれば、「5%以下で起こる稀なイベントが発生しており、差があると判断できる」と考えます。
サイコロを6回投げ、1の目が4回出る確率(またはより極端なケースの確率)は0.00866(0.87%)です。そのため5%以下の確率で発生するイベントであり、こうした稀なイベントが偶然発生するのはおかしいと考えます。こうして、有意差がある(サイコロにイカサマがある)と判断します。
連続型確率分布(確率密度関数)と累積分布関数の関係
ここまで、離散型確率分布を利用して累積分布関数を解説してきました。「確率を足すだけ」と理解すれば、誰でも累積分布関数の概念を理解できます。
次に連続型確率分布での累積分布関数を学びましょう。連続型確率分布とは、確率分布のグラフを描くときに曲線になるケースを指します。
例えば体重を測定するとき、60.0000kgぴったりの人は稀です。体重は60.0012kgとなるかもしれません。つまりコインやサイコロとは異なり、明確な値を出すことができません。そのため体重や身長など、こうしたケースでは連続型確率分布を利用します。
連続型確率分布の場合、離散型確率分布とは異なり明確な確率を得ることができません。そのため連続型確率分布では、面積を計算することによって確率を出します。これを確率密度といいます。
数学では、面積を計算する方法として積分を利用します。連続型確率分布で積分の公式が出るのは、面積を計算することによって確率を出すからなのです。そこで、連続型確率分布の確率密度(確率密度関数の値)を足していきましょう。そうすると、以下のグラフ(累積分布関数)になります。
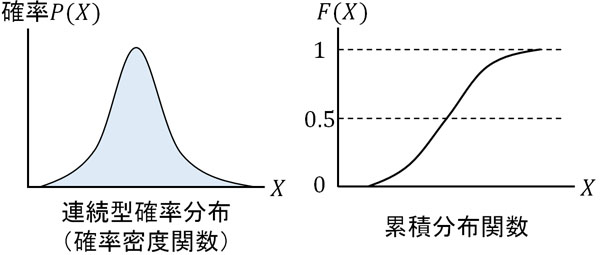
累積分布関数では確率を足すため、グラフの右側では確率が高くなります。またグラフの右端では、すべての確率を足すことによって1(100%)となります。これが連続型確率分布での累積分布関数です。
なお連続型確率分布で累積分布関数を考えるとき、統計学の教科書では以下の公式が出てきます。
- \(F(a)=\displaystyle \int_{-∞}^a p(x) dx\)
ただ、この公式を見ても意味を理解できないと思います。これは何を意味しているのでしょうか。\(F(a)\)というのは、連続型確率分布\(F(x)\)に対して、\(a\)を代入することを意味します。つまり、\(x=a\)のとき、\(a\)以下の確率密度(\(a\)以下の確率をすべて合計した値)を指します。
そこで、\(-∞\)(極限まで小さい値)から\(a\)までの面積を足しましょう。これを意味するのが\(\displaystyle \int_{-∞}^a\)です。図にすると、連続型確率分布では以下の部分の面積(確率)を指します。
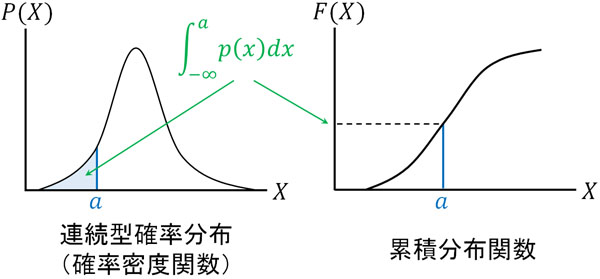
また累積分布関数では、すべての確率(面積)を足した値がたて軸となります。そのため\(x=a\)のときのたて軸を確認することによって、\(F(a)\)の値(すべての確率を足した値)を確認できます。
なお先ほどのグラフの関係より、確率密度関数(連続型確率分布での確率を計算する関数)を積分すると、累積分布関数になります。一方、累積分布関数を微分すると確率密度関数になります。
確率密度関数と累積分布関数の違いと正規分布との関係
ここまでの違いを理解すれば、確率密度関数と累積分布関数の違いが何か理解できるはずです。連続型確率分布での確率密度関数というのは、特定範囲の確率密度(起こる確率)を指します。一方で累積分布関数では、それまでの確率をすべて足すときの値を得られます。
また確率密度関数はほとんどの場合、正規分布となります。一つの山の形をした左右対称のグラフとなるのが連続型確率分布(確率密度関数)です。
一方で累積分布関数の場合、正規分布となることは確実にありません。確率を足すため、必ずグラフの形は右肩上がりになります。
ただ前述の通り、有意性の判定(差があるかどうかの判定)では累積分布関数を利用します。二項検定やz検定(標準正規分布を利用する検定)、t検定などを利用するとき、累積分布関数が重要になるのです。
正規分布に対する累積分布関数を利用し、0.05(5%)の確率で発生するイベントと比較することによって、差があるかどうかを確認するのが統計処理です。正規分布の確率密度関数と累積分布関数には、こうした関係があるのです。
累積分布関数の概念を学び、統計処理できるようにする
統計学で累積分布関数を学びます。私たちが統計学を学べば、有意差があるかどうか(差があるかどうか)を客観的に判断できるようになります。
有意差の判定では累積分布関数を利用します。特定のイベントが起こる確率だけでなく、より極端なイベントが起こる確率を含めて、すべての確率を足すのです。その後、0.05(5%)などの有意水準(差があるかどうか判定するポイント)と比較し、有意差の判定をします。そのため、累積分布関数は重要です。
累積分布関数は確率密度関数と異なります。確率密度関数を利用すると、多くの場合で正規分布となります。一方で累積分布関数では、正規分布となりません。また確率密度関数の面積を計算する(積分する)ことによって、累積分布関数を得ることができます。
累積分布関数の本質は「確率をすべて足すこと」です。この概念を学べば、累積分布関数への理解は完ぺきです。






