不定積分・定積分：公式や計算方法、微分との関係

微分の反対が積分になります。そのため積分を学ぶとき、事前に微分を理解しておく必要があります。そこで微分の反対を公式として覚えることにより、積分を行えるようになりましょう。

なお、特定の範囲を指定せずに積分をする場合、不定積分をすることになります。一方で特定の範囲について面積を知りたい場合、定積分をしましょう。積分によって、面積を得るための関数を得ることができます。具体的な面積を計算するとき、定積分を利用するのです。

このとき、不定積分や定積分の性質を覚えなければいけません。積分同士で足し算や引き算をするとき、どのように計算すればいいのか学ぶのです。

それでは、積分の公式には何があるのでしょうか。また、どのように積分をすればいいのでしょうか。公式を利用して積分を行う基本を解説していきます。

1 微分の逆により、不定積分を行う：不定積分の公式
- 1.1 不定積分の性質：定数倍と足し算・引き算のルール
2 特定の範囲を計算する定積分
3 積分の公式を覚え、答えを得られるようにする

微分の逆により、不定積分を行う：不定積分の公式

面積を得る関数を得たいとき、積分を利用します。微分と積分は親せきの関係にあり、微分の反対が積分に該当します。

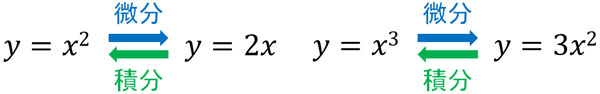
例えば\(f(x)=x^n\)を微分するとき、以下のようになります。

\(f'(x)=nx^{n-1}\)

そこで積分では、この反対を公式にすればいいとわかります。例えば\(f(x)=x^n\)を積分するとき、公式は以下です。

\(\displaystyle \int f(x) dx=\displaystyle\frac{1}{n+1}x^{n+1}+C\)

参考までに、\(\displaystyle\frac{1}{n+1}x^{n+1}+C\)を微分すると\(x^n\)を得られます。積分の公式を暗記するのではなく、微分と積分の関係を学ぶことで公式を利用できるようになりましょう。

積分の公式で\(+C\)が存在するのは、微分することによって0になるからです。具体的にどのような値が\(C\)に該当するのかについて、積分だけでは判断できません。\(C\)の値を知りたい場合、ほかの条件と比較する必要があります。

不定積分の性質：定数倍と足し算・引き算のルール

なお関数\(F(x)\)を微分することで関数\(f(x)\)を得られるとします。言い換えると、関数\(f(x)\)を積分すると関数\(F(x)\)を得られます。この場合、関数\(F(x)\)は\(f(x)\)の不定積分です。

それでは、実際に積分をすることによって不定積分の計算をしてみましょう。以下の問題の答えは何でしょうか。

\(\displaystyle \int (x-2)(x-3) dx\)

以下のように計算しましょう。

\(\displaystyle \int (x-2)(x-3) dx\)

\(=\displaystyle \int (x^2-5x+6) dx\)

\(=\displaystyle\frac{1}{3}x^3-\displaystyle\frac{5}{2}x^2+6x+C\)

こうして、公式を利用することによって積分することができました。

・定数倍するとき、数字を積分記号の中を入れられる（または外へ出せる）

なおかけ算や割り算（分数のかけ算）を式に含む場合、積分記号の中へ数字を入れることができます。例として、以下の問題を解きましょう。

\(2\displaystyle \int (x-2)(x-3) dx\)

以下のように計算します。

\(2\displaystyle \int (x-2)(x-3) dx\)

\(=\displaystyle \int 2(x-2)(x-3) dx\)

\(=\displaystyle \int 2(x^2-5x+6) dx\)

\(=\displaystyle \int (2x^2-10x+12) dx\)

\(=\displaystyle\frac{2}{3}x^3-5x^2+12x+C\)

このように計算することができます。なお、不定積分の定数倍を数式で表すと以下のようになります。

\(k\displaystyle \int f(x) dx=\displaystyle \int k·f(x) dx\)

定数倍に関する積分では、積分記号の中に数字を入れたり、反対に数字を積分記号の外に出したりすることができます。

・足し算や引き算では、不定積分を合体できる

それでは、不定積分の足し算・引き算はどのように考えればいいのでしょうか。足し算や引き算をする場合、積分記号を付けたまま関数同士の足し算・引き算をすることができます。例題として、以下の問題を解きましょう。

\(\displaystyle \int (x+2) dx+\displaystyle \int (x+4) dx\)

この式について、以下のように\(x+2\)と\(x+4\)を足し、そのあとに積分をしましょう。

\(\displaystyle \int (x+2) dx+\displaystyle \int (x+4) dx\)

\(=\displaystyle \int (x+2+x+4) dx\)

\(=\displaystyle \int (2x+6) dx\)

\(=x^2+6x+C\)

関数同士の足し算や引き算をすることができるため、計算は難しくありません。なお、数式で表すと以下のようになります。

\(\displaystyle \int f(x) dx+\displaystyle \int g(x) dx\)\(=\displaystyle \int \{f(x)+g(x)\} dx\)
\(m\displaystyle \int f(x) dx+n\displaystyle \int g(x) dx\)\(=\displaystyle \int \{m·f(x)+n·g(x)\} dx\)

公式を覚えるのではなく、計算方法を学びましょう。

特定の範囲を計算する定積分

なお不定積分として関数を得たとしても、面積を得ることはできません。面積を計算するためには、範囲を決める必要があります。例えば\(f(x)=2x\)について、積分をすると\(F(x)=x^2\)を得ることができます。

ただ不定積分\(F(x)=x^2\)について、\(x\)の範囲が\(0≦x≦1\)の場合と\(0≦x≦2\)の場合を比べると、得られる答え（面積）は異なると容易に理解できます。そこで、範囲を指定するのです。例えば以下の式というのは、関数\(f(x)=2x\)を積分し、\(0≦x≦1\)での面積を求めることを意味します。

\(\displaystyle \int_{0}^{1} (2x) dx\)

定積分の計算では、\(f(x)\)に対して積分をした後、\(x\)の範囲を用いて引き算をします。例えば\(f(x)\)を積分することにより、\(F(x)\)を得たとします。\(x\)の範囲が\(0≦x≦1\)なのであれば、\(F(1)\)から\(F(0)\)を引くことにより、面積を得ることができます。

定積分の計算をするとき、先ほどの式を以下のように表します。

\(\displaystyle \int_{0}^{1} (2x) dx=\left[x^2\right]_0^1\)

かっこの中に積分後の結果を記します。また、かっこの右に範囲を記載しましょう。その後、積分後の関数に値を代入することで引き算をします。先ほどの式（積分後の式）に値を代入し、\(F(1)\)から\(F(0)\)を引くと以下のようになります。

\(\left[x^2\right]_0^1\)

\(=1-0\)

\(=1\)

こうして\(y=2x\)について、\(x\)の範囲が\(0≦x≦1\)の場合、面積は1になるとわかりました。なお図を確認すると、たての長さが2、横の長さが1の直角三角形であるため、積分をしなくても答えは1とわかります。いずれにしても、積分をする場合と答えが一致するとわかります。

そこで、ここまでの計算を一般化しましょう。関数\(f(x)\)を積分することで\(F(x)\)を得ることができ、定積分の範囲が\(a\)から\(b\)までの場合、式は以下のように表されます。

\(\displaystyle \int_{a}^{b} f(x) dx\)\(=\left[F(x)\right]_a^b\)\(=F(b)-F(a)\)

知識なしに公式を見ても理解しにくいです。そこで、具体例を確認した後に公式の意味を学びましょう。

なお定積分の計算では、積分計算するときに\(+C\)を省略します。理由としては、引き算をするときに消去できるからです。例として、\(\displaystyle \int_{0}^{1} (2x) dx\)の計算をしてみましょう。

\(\displaystyle \int_{0}^{1} (2x) dx\)

\(\left[x^2+C\right]_0^1\)

\(=(1+C)-(0+C)\)

\(=1\)

こうして、先ほどと同じ答えになります。これが、定積分で\(+C\)を省略できる理由です。

定積分の性質と計算方法

定積分の性質は不定積分と同じです。そのため定数倍をするとき、積分記号の中に数字を入れることができます。

\(k\displaystyle \int_{a}^{b} f(x) dx\)\(=\displaystyle \int_{a}^{b} k·f(x) dx\)

また範囲が同じ場合、足し算や引き算をすることができます。

\(\displaystyle \int_{a}^{b} f(x) dx+\displaystyle \int_{a}^{b} g(x) dx\)\(=\displaystyle \int_{a}^{b} \{f(x)+g(x)\} dx\)
\(m\displaystyle \int_{a}^{b} f(x) dx+n\displaystyle \int_{a}^{b} g(x) dx\)\(=\displaystyle \int_{a}^{b} \{m·f(x)+n·g(x)\} dx\)

それでは、定積分に特有の性質には何があるのでしょうか。範囲が0の場合、面積は0です。そのため、以下の公式が成り立ちます。

\(\displaystyle \int_{a}^{a} f(x) dx=0\)

範囲が\(a\)から\(a\)であるため、答え（面積）がゼロになるのは当然です。また範囲が逆になる場合、マイナスを加えましょう。積分後の引き算の順番が逆になるため、等号でつなぐためにはマイナスを加える必要があるのです。

\(\displaystyle \int_{a}^{b} f(x) dx=-\displaystyle \int_{b}^{a} f(x) dx\)

なお面積を計算する方法が積分であるため、途中で範囲を区切ることができます。この場合、区切った場所を用いて足し算をしましょう。

\(\displaystyle \int_{a}^{b} f(x) dx\)\(=\displaystyle \int_{a}^{c} f(x) dx\)\(+\displaystyle \int_{c}^{b} f(x) dx\)

それでは、以下の式の答えを計算しましょう。

\(\displaystyle \int_{1}^{2} \left(x^3+\displaystyle\frac{1}{\sqrt{x}}\right) dx\)

公式を利用して計算すると、以下のようになります。

\(\displaystyle \int_{1}^{2} \left(x^3+\displaystyle\frac{1}{\sqrt{x}}\right) dx\)

\(=\displaystyle \int_{1}^{2} x^3 dx\)\(+\displaystyle \int_{1}^{2} x^{-\frac{1}{2}} dx\)

\(=\left[\displaystyle\frac{1}{3+1}x^{3+1}\right]_1^2\)\(+\left[\displaystyle\frac{1}{-\displaystyle\frac{1}{2}+1}x^{-\frac{1}{2}+1}\right]_1^2\)

\(=\left[\displaystyle\frac{1}{4}x^{4}\right]_1^2\)\(+\left[2x^{\frac{1}{2}}\right]_1^2\)

\(=\left[\displaystyle\frac{1}{4}x^{4}\right]_1^2\)\(+[2\sqrt{x}]_1^2\)

\(=\displaystyle\frac{1}{4}(2^4-1^4)+2(\sqrt{2}-1)\)

\(=\displaystyle\frac{7}{4}+2\sqrt{2}\)

こうして、定積分の計算を行うことができました。

定積分で表された関数の計算

それでは、定積分で表された関数を解けるようになりましょう。言い換えると、関数の中に積分を含む式の計算を行います。実際に例題を利用することで計算方法を学びましょう。

それでは、次の式を満たす\(f(x)\)は何でしょうか。

\(f(x)=x^2+2\displaystyle \int_{0}^{1} f(x) dx\)

積分の公式を利用するにしても、\(f(x)\)はこれから求めなければいけない式であるため、積分の公式を利用して直接計算することができません。

そこで、\(\displaystyle \int_{0}^{1} f(x) dx\)に着目しましょう。\(\displaystyle \int_{0}^{1} f(x) dx\)は特定の範囲の面積を示します。つまり、\(\displaystyle \int_{0}^{1} f(x) dx\)は定数です。

\(\displaystyle \int_{0}^{1} f(x) dx\)は明確な値であるため、\(\displaystyle \int_{0}^{1} f(x) dx=a\)としましょう。そうすると、以下のように表すことができます。

\(f(x)=x^2+2a\)

こうして、式は二次関数であるとわかりました。また\(f(x)=x^2+2a\)であるため、\(\displaystyle \int_{0}^{1} f(x) dx=a\)に代入することで計算しましょう。

\(\displaystyle \int_{0}^{1} f(x) dx=a\)

\(\displaystyle \int_{0}^{1} (x^2+2a) dx=a\)

\(\left[\displaystyle\frac{1}{3}x^3+2ax\right]_0^1=a\)

\(\left(\displaystyle\frac{1}{3}+2a\right)-0=a\)

\(a=-\displaystyle\frac{1}{3}\)

\(a=-\displaystyle\frac{1}{3}\)とわかったため、\(f(x)=x^2-\displaystyle\frac{2}{3}\)と計算できました。

範囲に変数を含む積分と関数：微分の利用

定積分の計算では、定積分と微分の関係を利用した問題もひんぱんに出題されます。定積分の範囲に変数を含む場合、微分することで関数を計算しましょう。

前述の通り、微分と積分は親せき関係にあります。積分した関数を微分すると、関数は元に戻ります。それでは、「定積分を微分する場合」はどうなるでしょうか。先ほどの問題で確認した通り、定積分は定数です。定数を微分すると0になります。例として、\(\displaystyle \int_{1}^{0} (2x+1) dx\)を計算しましょう。

\(\displaystyle \int_{1}^{0} (2x+1) dx\)

\(=\left[x^2+x\right]_0^1\)

\(=(1+1)-0\)

\(=2\)

2に対して\(x\)で微分すると0になります。それでは、\(\displaystyle \int_{1}^{x} (2t+1) dt\)を微分する場合はどうでしょうか。先ほどとは異なり、定積分の範囲に変数\(x\)を含みます。この場合、微分をすることで\(2x+1\)になります。

実際に計算をして確認しましょう。

\(\displaystyle \int_{1}^{x} (2t+1) dt\)

\(=\left[t^2+t\right]_0^x\)

\(=(x^2+x)-0\)

\(=x^2+x\)

\(x^2+x\)を微分すると\(2x+1\)になります。このように、定積分の計算で範囲に変数を含む場合、微分することによって積分記号を取り去ることができるとわかります。そのため\(\displaystyle \int_{a}^{x} f(t) dt\)や\(\displaystyle \int_{x}^{a} f(t) dt\)のように、範囲に変数\(x\)を含む場合は微分を利用して計算しましょう。

それでは、以下の等式を満たす関数\(f(x)\)と定数\(a\)の値を求めましょう。