数学で必ず理解しなければいけない内容に弧度法(ラジアン)と三角関数があります。物理では三角関数を利用して計算する場面がひんぱんにあります。そのため数学だけでなく、物理でも三角関数は重要な学習内容です。
また角度を利用するとき、物理で度数法を利用することはほとんどありません。度数法の代わりとして、弧度法を用いて計算します。そのため数学で弧度法を理解していない場合、物理の問題も解けません。
数学で三角関数が重要な理由は、ほかの学習分野でもひんぱんに利用されるからです。そこで弧度法に慣れ、三角関数を用いて計算できるようになりましょう。
それでは、どのように弧度法を用いて角度を計算すればいいのでしょうか。また、三角関数の性質やグラフはどのようになるのでしょうか。弧度法と三角関数について、考え方や計算方法を解説していきます。
もくじ
度数法と弧度法(ラジアン)の変換
私たちが小学校で角度を学ぶとき、30°や90°などの度数法を利用して角度を表します。円の中心の一周は360°であり、直角は90°です。
ただ角度を利用して計算問題を解くとき、数学や物理では度数法ではなく、弧度法を利用する場面が多いです。弧度法では、\(360°=2π\)と考えます。そのため、以下のようになります。
- \(30°=\displaystyle\frac{π}{6}\)
- \(45°=\displaystyle\frac{π}{4}\)
- \(60°=\displaystyle\frac{π}{3}\)
- \(90°=\displaystyle\frac{π}{2}\)
- \(180°=π\)
弧度法では、\(180°=π\)となることを覚えましょう。また度数法での角度が減少すると、弧度法でも同じ割合で値が減少します。例えば\(180°÷6=30°\)です。そのため、30°を弧度法で表すと\(\displaystyle\frac{π}{6}\)になります。
このように、度数法を弧度法へ変換できるようになりましょう。反対に、弧度法を度数法へ変換できるようになりましょう。
扇形の弧の長さと面積の計算
それでは、なぜ弧度法を利用して角度を表す必要があるのでしょうか。度数法ではなく、弧度法を利用すると、扇形や円を利用して計算するときに便利です。扇形の弧の長さと半径による比に着目して角度を表す方法が弧度法です。
半径\(r\)の円では、円周の長さは\(2πr\)です。そこで、前述の通り\(360°=2π\)と設定しましょう。このとき、円周の長さは弧度法での角度の大きさによって変化します。以下のようになります。
- \(30°:\displaystyle\frac{π}{6}r\)
- \(45°:\displaystyle\frac{π}{4}r\)
- \(60°:\displaystyle\frac{π}{3}r\)
- \(90°:\displaystyle\frac{π}{2}r\)
- \(180°:πr\)
- \(360°:2πr\)
扇形の弧の長さは角度の大きさに比例するため、この関係が成り立ちます。そこで扇形の弧の長さを\(l\)、弧度法での角度を\(θ\)とすると、以下の公式が成り立ちます。
- \(l=rθ\)
当たり前の内容を表している公式ですが、このように弧度法を利用すると、弧の長さの計算が楽です。弧度法での角度というのは、弧の長さと密接な関係があるのです。
・弧度法を利用して扇形の面積を得る
次に、弧度法を用いて扇形の面積を計算できるようになりましょう。円周と同じように、面積も角度に比例します。そのため扇形の面積を\(S\)、角度を\(θ\)とすると、円の面積は\(r^2π\)であるため、以下の関係が成り立ちます。
- \(r^2π:S=2π:θ\)
そこで、以下のようにこの式を計算しましょう。
\(2πS=r^2πθ\)
\(S=\displaystyle\frac{1}{2}r^2θ\)
こうして、公式として\(S=\displaystyle\frac{1}{2}r^2θ\)を得ることができました。また\(l=rθ\)であるため、公式を以下のように変形することもできます。
- \(S=\displaystyle\frac{1}{2}rl\)
扇形の面積を得る公式を覚える必要はありません。ここに記した通り、簡単な計算によって公式を導出できるからです。
弧度法を利用して三角関数を表す
弧度法による角度の意味を理解したら、弧度法を利用して三角関数を表せるようになりましょう。例えば\(30°=\displaystyle\frac{π}{6}\)をsinθやcosθ、tanθで表すと以下のようになります。
- \(sin\displaystyle\frac{π}{6}=\displaystyle\frac{1}{2}\)
- \(cos\displaystyle\frac{π}{6}=\displaystyle\frac{\sqrt{3}}{2}\)
- \(tan\displaystyle\frac{π}{6}=\displaystyle\frac{1}{\sqrt{3}}\)
三角比を学んでおり、度数法での計算を行える場合、この計算については問題なく行えると思います。sinθ、cosθ、tanθの値を得るとき、弧度法を度数法に直すと計算しやすいです。
また弧度法では、三角比で学んだ以下の公式を利用できます。
- \(sin^2θ+cos^2θ=1\)
- \(tanθ=\displaystyle\frac{sinθ}{cosθ}\)
- \(1+tan^2θ=\displaystyle\frac{1}{cos^2θ}\)
度数法も弧度法も概念は同じであり、角度の表記法が違うだけです。そのため、利用する公式は同じです。
角度の変化による三角関数の変化
それでは、角度の変化によってどのように三角関数が変わるのか確認しましょう。角度を足したり引いたりすることにより、三角比が変化することを既に学んでいると思います。例えば、以下の図があるとします。
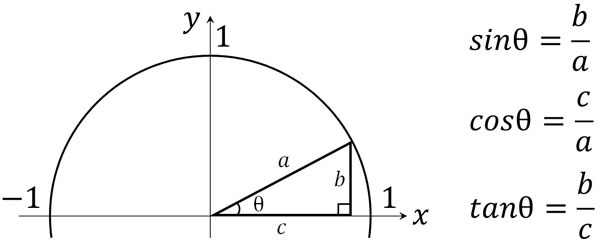
この図について、三角比では以下の関係が成り立ちます。
- \(sin(90°-θ)=cosθ\)
- \(cos(90°-θ)=sinθ\)
- \(tan(90°-θ)=\displaystyle\frac{1}{tanθ}\)
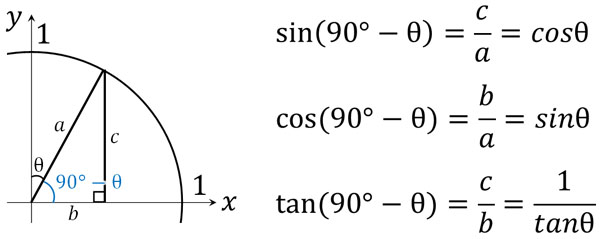
弧度法であっても、同じように角度を足したり引いたりすることによって値が変化します。図を利用すれば、どのように値が変化するのかわかります。
・\(θ+2πn\)の三角関数:\(n\)は整数
前述の通り、\(360°=2π\)です。そのため、例えば\(3π=π\)であり、\(\displaystyle\frac{9}{2}π=\displaystyle\frac{1}{2}π\)です。角度が\(θ+2πn\)(\(n\)は整数)のとき、角度を\(θ\)と考えて計算することができます。
・\(-θ\)の三角関数
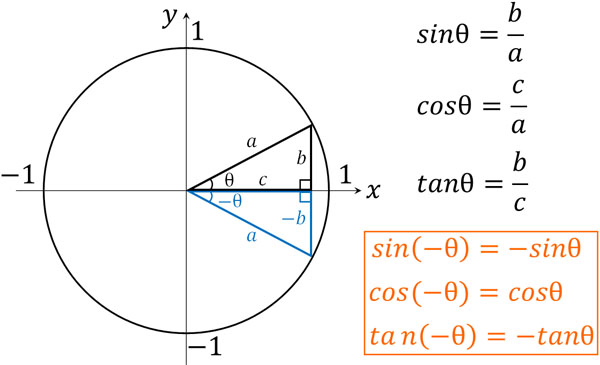
\(-θ\)となる場合、\(θ\)に比べて\(x\)軸の座標は変化しません。一方、\(y\)座標の符号はプラスからマイナス(またはマイナスからプラス)へと変化します。そのため、以下のように変化します。
- \(sin(-θ)=-sinθ\)
- \(cos(-θ)=cosθ\)
- \(tan(-θ)=-tanθ\)
・\(θ+π\)の三角関数
角度に対して\(π\)を足すというのは、180°が加わることを意味しています。θに対して180°を足すとき、三角関数は以下のように変化します。
- \(sin(θ+π)=-sinθ\)
- \(cos(θ+π)=-cosθ\)
- \(tan(θ+π)=tanθ\)
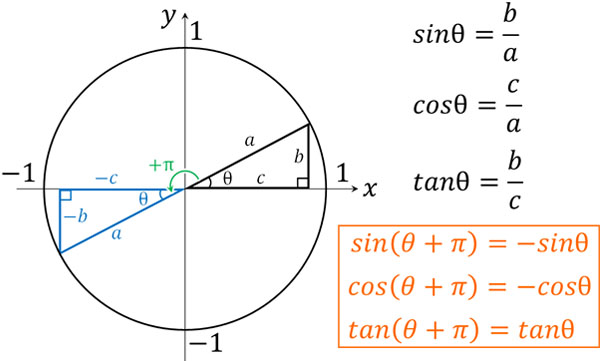
図を確認すれば、なぜこのように変化するのか理解できます。図を描かないとわからないため、毎回図を利用することで三角関数を変換できるようになりましょう。
・\(θ+\displaystyle\frac{π}{2}\)の三角関数
角度が\(\displaystyle\frac{π}{2}\)加わるというのは、90°を足すことを意味しています。角度が90°変化するとき、三角関数は以下のように変わります。
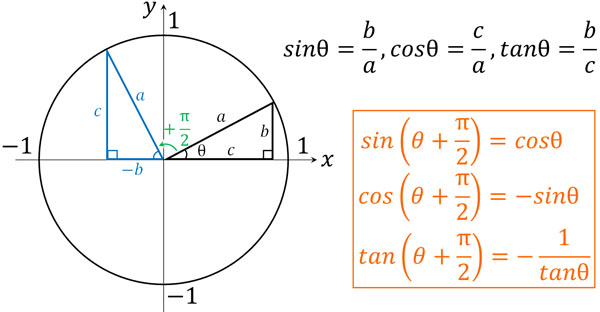
公式を覚えるのではなく、図を利用することによって三角関数を変換できるようになりましょう。
三角関数のグラフ:sinθ、cosθ、tanθ
三角関数で重要な内容の一つにグラフがあります。特に物理では、前述の通り三角関数を利用して問題を解くことがひんぱんにあります。三角関数でグラフを理解していない場合、数学だけでなく、物理の問題を解くこともできません。そこで、三角関数による角度の変化と図形の様子を学びましょう。
・sinθの図形
sinθの範囲は\(-1≦sinθ≦1\)です。また角度とsinθの値を確認すると以下のようになります。
- \(sin0=0\)
- \(sin\displaystyle\frac{π}{2}=1\)
- \(sinπ=0\)
- \(sin\displaystyle\frac{3π}{2}=-1\)
そこで、角度とsinθの値をグラフにしましょう。以下のようになります。
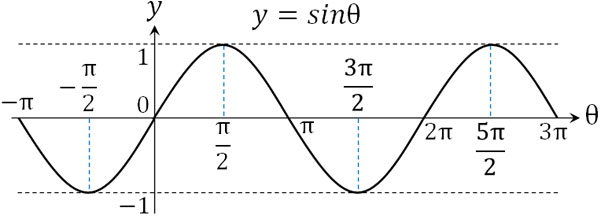
・cosθの図形
cosθの範囲は\(-1≦cosθ≦1\)です。角度とcosθの値は以下のようになります。
- \(cos0=1\)
- \(cos\displaystyle\frac{π}{2}=0\)
- \(cosπ=-1\)
- \(cos\displaystyle\frac{3π}{2}=0\)
sinθとは異なり、\(θ=0\)のとき、\(y\)の値は1です。角度の変化による\(y\)の値を図示すると以下のようになります。
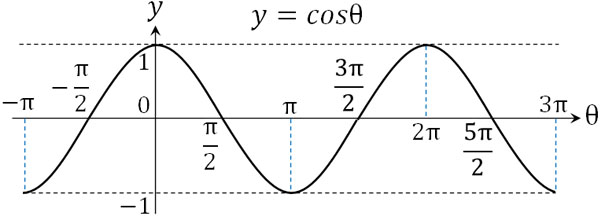
・tanθの図形
sinθやcosθとは異なり、tanθでは1よりも大きい値(または1よりも小さい値)となるケースがひんぱんにあります。またtanθでは、\(θ=90°=\displaystyle\frac{π}{2}\)のとき、値が無限大になります。同様に\(θ=-90°=-\displaystyle\frac{π}{2}\)のとき、tanθの値はマイナスに無限大となります。
つまり、tanθは\(-\displaystyle\frac{π}{2}<θ<\displaystyle\frac{π}{2}\)で一つの区切りです。以下がtanθの図形です。
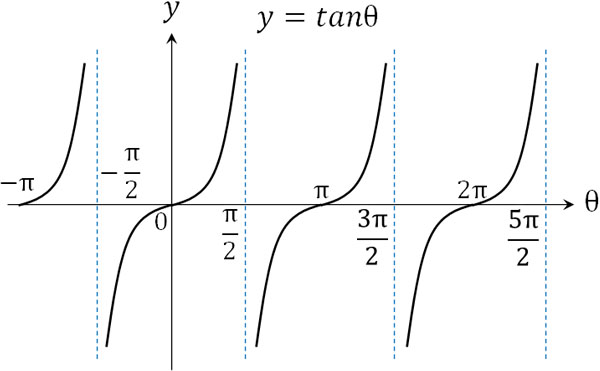
三角関数のグラフの平行移動と拡大・縮小
三角関数のグラフでは、角度の変化による平行移動やグラフの拡大・縮小を学びましょう。物理では円運動や波動、電磁気でひんぱんに三角関数のグラフが利用されるため、必ず理解しなければいけない内容です。
・角度の変化とグラフの平行移動
まず、グラフの平行移動を確認しましょう。例えば、以下のグラフはどのように描けばいいでしょうか。
- \(y=sin\left(θ-\displaystyle\frac{π}{2}\right)\)
\(θ=\displaystyle\frac{π}{2}\)の場合、\(y=sin\left(θ-\displaystyle\frac{π}{2}\right)\)の値は0になります。つまり\(sinθ\)のグラフに対して、θ方向に\(\displaystyle\frac{π}{2}\)平行移動した図が\(y=sin\left(θ-\displaystyle\frac{π}{2}\right)\)です。
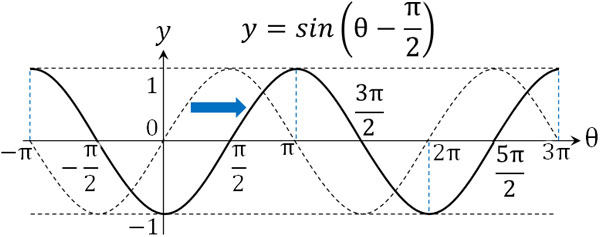
図を確認すると、\(y=sin\left(θ-\displaystyle\frac{π}{2}\right)\)は\(y=-cosθ\)と同じとわかります。角度が\(\displaystyle\frac{π}{2}\)ずれる場合、sinθをcosθへ変えることができます。また条件によっては、cosθをsinθへ変換することも可能です。
・グラフの拡大・縮小
\(y=asinθ\)のグラフでは、\(y=sinθ\)のグラフに対して大きさが\(a\)倍となります。例えば\(y=2sinθ\)の場合、大きさは\(y=sinθ\)の2倍となります。具体的には、\(-2≦y≦2\)となります。一方で\(y=\displaystyle\frac{1}{2}sinθ\)の場合、大きさは\(y=sinθ\)の\(\displaystyle\frac{1}{2}\)倍となります。
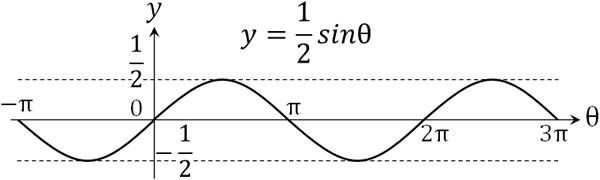
・周期の変化
sinθとcosθでは、同じ運動が繰り返されます。このとき、元の場所に戻るまでの期間を周期といいます。例えばsinθの周期は\(2π\)です。\(2π\)が経過すると、元の場所に戻るからです。
それでは、\(sinkθ\)の周期はどうなるでしょうか。例えば\(sin2θ\)では、\(θ=π\)のとき、\(2π\)進むことになります。つまり周期は\(π\)であり、\(2π\)のときに比べて周期はθ軸方向に\(\displaystyle\frac{1}{2}\)となります。
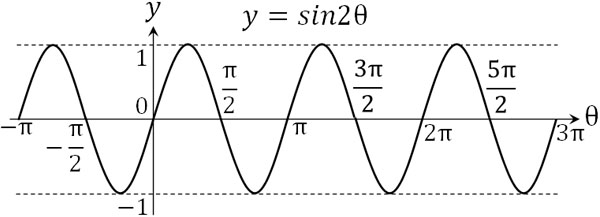
一方で\(sin\displaystyle\frac{θ}{2}\)では、\(θ=4π\)のとき、\(2π\)進むことになります。つまり周期は\(4π\)であり、周期が\(2π\)のときに比べて、周期はθ軸方向に2倍となります。
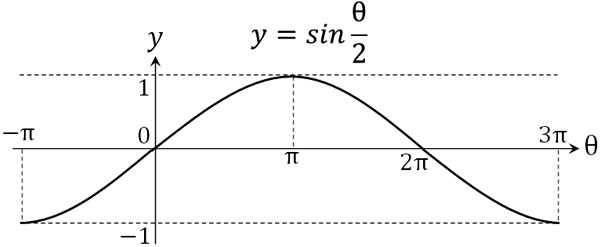
\(sinkθ\)では、\(\displaystyle\frac{1}{k}\)倍に周期が拡大または縮小することになります。\(k\)倍ではないことに注意しましょう。三角関数のグラフについて、平行移動や拡大・縮小は基本的な内容の一つであるため、必ず理解できるようになりましょう。
三角関数の基本と弧度法を学ぶ
私たちにとって度数法のほうが身近です。ただ数学や物理では、度数法ではなく弧度法を利用するケースが多いです。特に物理では、弧度法を理解していないと計算問題を解くことができません。そこで、度数法と弧度法の両方を利用できるようになりましょう。
扇形の弧の長さに着目して角度を表す方法が弧度法です。そのため弧度法を利用すれば、扇形の弧の長さや面積を計算できます。
また弧度法を利用して三角関数を表せるようになりましょう。度数法を用いる三角比と内容は同じであり、弧度法を用いてsinθやcosθ、tanθを表記するのです。このときグラフを描けるようになり、平行移動や拡大・縮小、周期の計算を行えるようになりましょう。
ここまで、弧度法を用いる三角関数を解説してきました。すべて基本的な内容であるため、必ず内容を理解しましょう。






