微分をすることによって、新たな関数(導関数)を得ることができます。導関数を利用することによって、三次関数の極大値と極小値を求めることができます。
極大や極小となる場所がわかれば、三次関数の最大値と最小値を求められるようになります。このとき\(x\)の範囲が変化することによって、最大値と最小値が変わります。そのため、どのような条件のときに最大値や最小値になるのか理解しましょう。
また応用問題として三角関数や指数関数、対数関数の最大値と最小値を計算できるようになりましょう。文字の置き換えをしたり、\(x\)の範囲を求めたりすることによって最大値と最小値がわかるようになります。
最大値と最小値を見つけるためには、計算方法を覚えなければいけません。そこで、どのように三次関数の最大値と最小値を求めればいいのか解説していきます。
もくじ
導関数を利用し、三次関数の最大値と最小値を求める
\(α≦x≦β\)のとき、三次関数の最大値と最小値を問われる問題が頻繁に出題されます。極値をもたない三次関数の場合、最大値と最小値を答えるのは簡単です。一方で極値をもつ三次関数では、どこが最大値や最小値になるのか確認しなければいけません。
まず、三次関数の最大値を理解しましょう。極値をもつ三次関数について、最大値は極大値、範囲の左端、範囲の右端のどこかです。
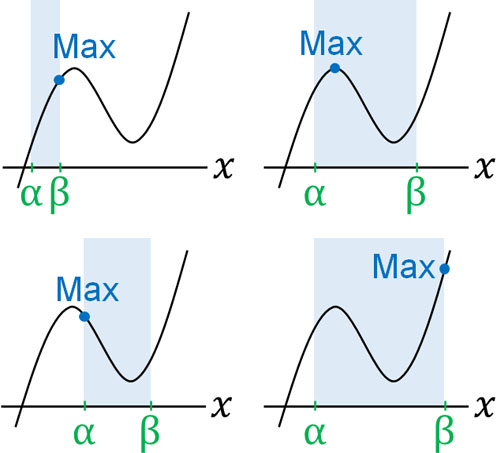
そのため最大値を見つけるためには、極大値や左端、右端に着目すればいいとわかります。
最小値を探す方法も考え方は同じです。三次関数の極小値と左端、右端を確認し、最小値がどこになるのか見つけましょう。
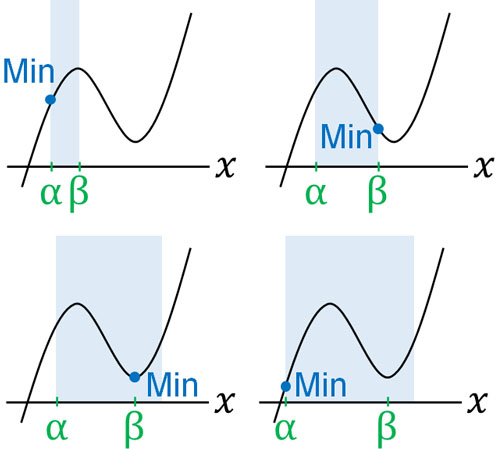
いずれにしても最大値と最小値を見つけるためには、極大値と極小値を求めなければいけません。極大値と極小値を探すには、微分することによって導関数を得る必要があります。そのため、三次関数の最大値と最小値に関する問題が出されたとき、まずは微分しましょう。
例えば、以下の問題の答えは何でしょうか。
- \(f(x)=x^3-6x^2+9x+2\)の三次関数について、\(-1≦x≦4\)のとき、最大値と最小値の値は何でしょうか。
微分することによって、まずは導関数を求めましょう。以下のようになります。
- \(f'(x)=3x^2-12x+9\)
また\(f'(x)=0\)となる値を探すことによって、極大値と極小値がわかるようになります。そこで因数分解しましょう。
\(3x^2-12x+9=0\)
\(3(x^2-4x+3)=0\)
\(3(x-1)(x-3)=0\)
こうして\(x=1\)のときに極大値、\(x=3\)のときに極小値になるとわかります。また\(-1≦x≦4\)であるため左端\(f(-1)\)、極大値\(f(1)\)、極小値\(f(3)\)、右端\(f(4)\)について、\(f(x)\)の値を出しましょう。以下のようになります。
\(f(-1)=-1-6-9+2=-14\)
\(f(1)=1-6+9+2=6\)
\(f(3)=27-54+27+2=2\)
\(f(4)=64-96+36+2=6\)
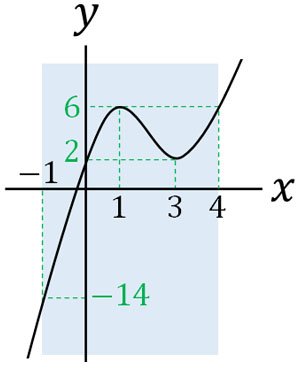
こうして\(-1≦x≦4\)のとき最大値は6、最小値は14であるとわかります。
最大値を求める文章題の問題
なお三次関数の最大値を答える問題について、文章題で出されることもあります。そこで、文章から式を作れるようにしましょう。例えば、以下の問題の答えは何でしょうか。
- 半径\(a\)の球に接する円柱について、体積が最大となるとき、最大値とそのときの高さを求めましょう。
半径\(a\)の球に接する円柱を実際に描いてみましょう。円(円柱の底面)の半径を\(b\)、円柱の半分の高さを\(h\)とすると以下のようになります。

円柱の底面の半径は\(b\)であり、円柱の高さは\(2h\)です。そのため、円柱の体積は以下のように計算できます。
\(b^2×π×2h=2πb^2h\)
また三平方の定理より、\(a^2=b^2+h^2\)です。つまり、\(b^2=a^2-h^2\)です。そこで、先ほどの式に代入しましょう。体積\(V\)は以下の式になります。
\(V=2πb^2h\)
\(=2πh(a^2-h^2)\)
\(=-2πh^3+2πa^2h\)
この式は\(h\)(高さ)が変化することによって、体積\(V\)が変わる関数と考えることができます。そこで、\(h\)を基準に微分しましょう。以下のようになります。
\(V’=-6πh^2+2πa^2\)
\(V’=-2π(3h^2-a^2)\)
\(V’=-2π(\sqrt{3}h+a)(\sqrt{3}h-a)\)
こうして、\(h=-\displaystyle\frac{a}{\sqrt{3}}\)または\(h=\displaystyle\frac{a}{\sqrt{3}}\)のとき、三次関数\(V\)は傾きがゼロになります。また\(0<h<a\)\((a>0)\)であるため、\(h=-\displaystyle\frac{a}{\sqrt{3}}\)は不適です。そのため、極大値となる\(h=\displaystyle\frac{a}{\sqrt{3}}\)を利用しましょう。
また最大値を確認するとき、極値と範囲の左端、範囲の右端を確認すればいいです。このとき、\(h\)の値が0や\(a\)のとき、体積\(V\)は0になります。そのため、以下のグラフを描くことができます。
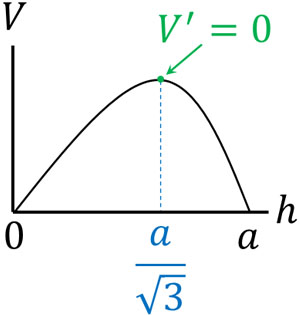
そのため\(h=\displaystyle\frac{a}{\sqrt{3}}\)のとき、体積は最大となります。高さは\(2h\)なので、体積が最大となる高さは\(\displaystyle\frac{2a}{\sqrt{3}}\)です。
また\(h=\displaystyle\frac{a}{\sqrt{3}}\)を代入することによって体積を計算できます。
\(V=-2πh^3+2πa^2h\)
\(V=-2π\left(\displaystyle\frac{a}{\sqrt{3}}\right)^3+2πa^2\left(\displaystyle\frac{a}{\sqrt{3}}\right)\)
\(V=-\displaystyle\frac{2}{3\sqrt{3}}πa^3+\displaystyle\frac{2}{\sqrt{3}}πa^3\)
\(V=\displaystyle\frac{4}{3\sqrt{3}}πa^3\)
\(V=\displaystyle\frac{4\sqrt{3}}{9}πa^3\)
文章題の場合、今回のようにあなたが円柱の高さや円柱の底面の半径を設定し、問題を解かなければいけません。
文字を含み、極値が動く場合の三次関数の最大値と最小値
次に、文字を含む三次関数の最大値と最小値を求められるようにしましょう。式に文字を含むというのは、極値が移動することを意味します。極値が移動する場合、最大値と最小値が変わります。
例えば、以下の問題の答えは何でしょうか。
- \(f(x)=x^3-6ax^2+9a^2x\)について、\(a\)が正の定数の場合、\(0≦x≦1\)での最大値はいくらでしょうか。
最大値を求めるためにはグラフの極値を求め、グラフを描く必要があります。そこで以下のように微分しましょう。
\(f'(x)=3x^2-12ax+9a^2\)
\(f'(x)=3(x^2-4ax+3a^2)\)
\(f'(x)=3(x-3a)(x-a)\)
こうして、\(x=a,3a\)のときに極値となります。また\(f(a)\)と\(f(3a)\)は以下のようになります。
\(f(a)=a^3-6a^3+9a^3=4a^3\)
\(f(3a)=27a^3-54a^3+27a^3=0\)
そのため、以下のようなグラフを描くことができます。

次に\(0≦x≦1\)のとき、\(a\)の値によって最大値がどのように変化するのか考えましょう。以下の3パターンに分けることができます。
・\(1<a\)の場合
まず、\(1<a\)の場合を考えてみましょう。この場合、\(0≦x≦1\)なので\(x\)の範囲は\(a\)の値よりも小さくなります。グラフを描くと、以下のようになります。
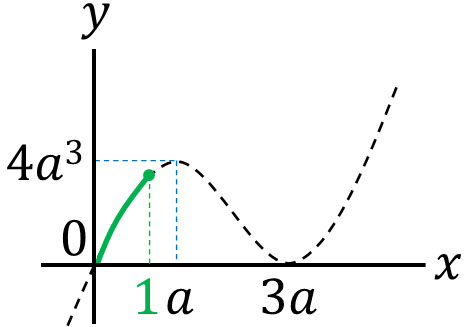
つまり、\(f(1)\)のときに最大値となります。そこで、\(x=1\)を代入しましょう。\(f(1)=1-6a+9a^2\)であるため、これが最大値です。
・\(f(x)=4a^3\)になる\(x\)の値を求める
次に、\(f(x)=4a^3\)となる\(x\)の値を求めましょう。\(f(a)=4a^3\)であることは既に述べましたが、\(f(x)=4a^3\)となるもう一つの\(x\)の値を見つけるのです。\(y\)の値が\(4a^3\)よりも大きいのか、それとも小さいのかによって以下のように最大値が変わります。
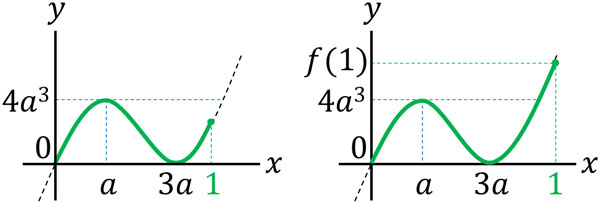
\(f(x)=x^3-6ax^2+9a^2x\)であるため、答えが\(4a^3\)となるためには、以下の方程式を作ればいいです。
\(x^3-6ax^2+9a^2x=4a^3\)
\(x^3-6ax^2+9a^2x-4a^3=0\)
どのようにすれば、この式を因数分解できるでしょうか。\(x=a\)のとき、\(f(a)=4a^3\)になると既にわかっています。また\(x=a\)のとき、グラフより\(f(x)\)の曲線と\(y=4a^3\)(\(x\)軸に平行の直線)は接します。
これはつまり、重解をもつことを意味します。重解をもつため、因数分解することによって\((x-a)^2\)を式の中にもたなければいけません。
つまり、以下のように変形できます。
\(x^3-6ax^2+9a^2x-4a^3=0\)
\((x-a)^2(x-A)=0\)
\((x^2-2ax+a^2)(x-A)=0\)
それでは\(x^3-6ax^2+9a^2x-4a^3\)と\((x-2a+a^2)(x-A)\)を比べて、Aがどのような値であれば条件を満たすでしょうか。\(A=4a\)であると、\(a^2×-4a=-4a^3\)となるため、条件を満たすような気がします。そこで、以下の式を作りましょう。
\((x^2-2ax+a^2)(x-4a)=0\)
このようにして、因数分解することができました。
\((x^2-2ax+a^2)(x-4a)=0\)
\((x-a)^2(x-4a)=0\)
つまり\(x=a,4a\)のとき、\(f(x)=4a^3\)になります。
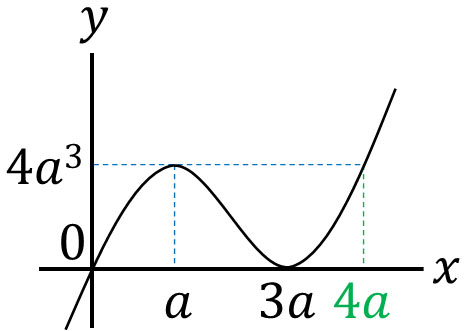
\(x=4a\)に対して、\(x\)の値が大きいのか、それとも小さいのかによって最大値が変化します。そこで、以下のように場合分けましょう。
・\(1≦4a\)かつ\(a≦1\)、つまり\(\displaystyle\frac{1}{4}≦a≦1\)の場合
\(\displaystyle\frac{1}{4}≦a≦1\)のとき、\(0≦x≦1\)であるため、極大値\(f(a)\)で最大値となります。そのため、最大値は\(f(a)=4a^3\)です。
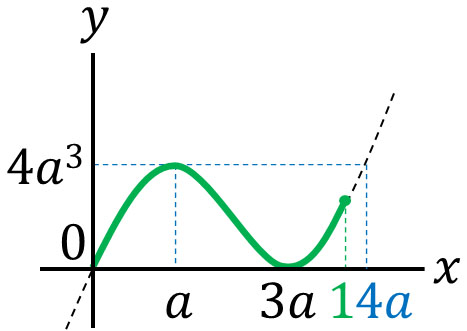
・\(4a<1\)、つまり\(0<a<\displaystyle\frac{1}{4}\)のとき
\(0<a<\displaystyle\frac{1}{4}\)のとき、極大値は\(f(1)\)です。つまり、最大値は\(f(1)=1-6a+9a^2\)です。
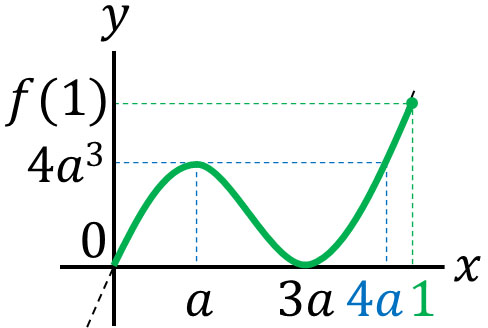
こうして、以下が答えであるとわかります。
- \(0<a<\displaystyle\frac{1}{4}\)、\(1<a\)の場合:最大値は\(1-6a+9a^2\)
- \(\displaystyle\frac{1}{4}≦a≦1\)の場合:最大値は\(4a^3\)
極値が動くとき、場合分けすることによって答えを出しましょう。
三角関数を含む場合、文字を置き換えする
なお、場合によっては三角関数を含むことがあります。このときは置き換えを利用して三角関数を計算しましょう。例えば、以下の答えは何になるでしょうか。
- \(y=sin3x+4cos2x+8sinx\)について、\(0≦x≦π\)のとき、最大値と最小値を求めましょう。
まず、3倍角の公式と2倍角の公式を利用しましょう。
\(sin3x=3sinx-4sin^3x\)
\(cos2x=1-2sin^2x\)
そのため、以下のように式を変形できます。
\(y=sin3x+4cos2x+8sinx\)
\(y=3sinx-4sin^3x\)\(+4(1-2sin^2x)\)\(+8sinx\)
\(y=-4sin^3x\)\(-8sin^2x+11sinx+4\)
次に、\(sinx=t\)に置き換えましょう。文字の置き換えをすることによって、これまで活用してきた微分を行いやすくなります。
\(y=-4t^3-8t^2+11t+4\)
三次関数で最大値と最小値を得るためには、微分することによって極大値や極小値、左端、右端の値を出せばいいです。微分すると以下のようになります。
\(y=-12t^2-16t+11\)
\(y=-(12t^2+16t-11)\)
\(y=-(2t-1)(6t+11)\)
こうして、\(t=-\displaystyle\frac{11}{6}\)のときに極小値、\(t=\displaystyle\frac{1}{2}\)のときに極大値を取るとわかります。
また\(0≦x≦π\)であるため、\(0≦sinx≦1\)です。つまり、\(0≦t≦1\)です。そこで\(f(t)=-4t^3-8t^2+11t+4\)について、左端\(f(0)\)と極大値\(f\left(\displaystyle\frac{1}{2}\right)\)、右端\(f(1)\)の値を確認しましょう。以下のようになります。
\(f(0)=4\)
\(f\left(\displaystyle\frac{1}{2}\right)=-4×\displaystyle\frac{1}{8}\)\(-8×\displaystyle\frac{1}{4}\)\(+11×\displaystyle\frac{1}{2}\)\(+4\)\(=7\)
\(f(1)=-4-8+11+4=3\)
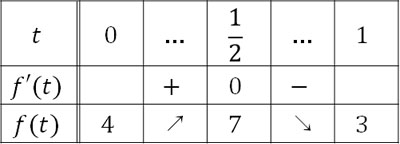
こうして\(t=\displaystyle\frac{1}{2}\)、つまり\(x=\displaystyle\frac{1}{6}π,\displaystyle\frac{5}{6}π\)のとき、最大値7となります。また\(t=1\)、つまり\(x=\displaystyle\frac{1}{2}π\)のとき、最小値3となります。
変域に注意し、指数関数で文字の置き換えをする
なお三角関数だけでなく、指数関数についても文字の置き換えをすることによって最大値と最小値を計算することができます。複雑な式を計算する場合、文字の置き換えは非常に有効な方法です。
例えば、以下の答えは何でしょうか。
- \(y=8^x-6×4^x+9×2^x+1\)について、\(x≦2\)のとき、最大値と最小値を求めましょう。
問題の解き方は先ほどと同じであり、文字の置き換えをしましょう。具体的には、\(2^x=t\)としましょう。そうすると、以下の式を作ることができます。
\(y=8^x-6×4^x+9×2^x+1\)
\(y=2^{3x}-6×2^{2x}+9×2^x+1\)
\(y=t^3-6t^2+9t+1\)
三次関数の最大値と最小値を求めるため、微分をしましょう。以下のようになります。
\(y’=3t^2-12t+9\)
\(y’=3(t^2-4t+3)\)
\(y’=3(t-1)(t-3)\)
こうして\(t=1\)のとき極大値となり、\(t=3\)のとき極小値になるとわかります。また\(x≦2\)であるため、\(0<2^x≦4\)です。つまり\(0<t≦4\)です。そこで\(f(t)=t^3-6t^2+9t+1\)について極大値や極小値、左端、右端の値を調べましょう。
\(f(0)=1\)
\(f(1)=1-6+9+1=5\)
\(f(3)=27-54+27+1=1\)
\(f(4)=64-96+36+1=5\)
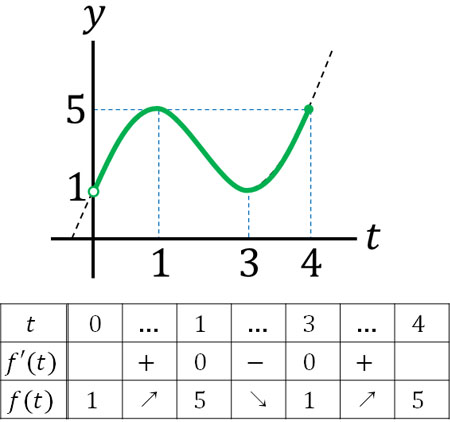
こうして\(t=1\)または\(t=4\)のとき、つまり\(x=0\)または\(x=2\)のとき、最大値5になります。また\(0<t≦4\)であるため、\(t=3\)のとき、つまり\(x=log_23\)のとき、最小値1になります。
対数関数では\(x\)の範囲を求め、関数を作る
次に対数関数の最大値と最小値を求めてみましょう。対数関数についても、文字の置き換えによって問題を解けるケースがあります。
ただ三次関数が関わる対数関数については、最初に\(x\)の範囲を出しましょう。その後、三次関数の形にすることによって最大値と最小値を求めます。例えば、以下の答えは何でしょうか。
- \(y=log_3x+2log_3(6-x)\)について、最大値とそのときの\(x\)の値を求めましょう。
真数条件より\(x>0\)です。また真数条件より\(6-x>0\)、つまり\(x<6\)です。そのため、\(x\)の範囲は\(0<x<6\)です。
次に最大値を求めるため、対数の中に三次関数を作りましょう。以下のようになります。
\(y=log_3x+2log_3(6-x)\)
\(y=log_3x+log_3(6-x)^2\)
\(y=log_3x(x^2-12x+36)\)
\(y=log_3(x^3-12x^2+36x)\)
仮に\(y=log_3f(x)\)とすると、以下のようになります。
\(log_3f(x)=log_3(x^3-12x^2+36x)\)
底は3であるため、\(f(x)\)の値が大きくなると\(y\)の値も大きくなります。そのため\(f(x)\)の値がどのように変化するのかを確認し、最大値を求めればいいとわかります。
\(f(x)=x^3-12x^2+36x\)であるため、最大値を求めるために微分しましょう。以下のようになります。
\(f'(x)=3x^2-24x+36\)
\(f'(x)=3(x^2-8x+12)\)
\(f'(x)=3(x-2)(x-6)\)
そのため\(x=2\)のとき極大値となり、\(x=6\)のとき極小値となります。また\(0<x<6\)であるため、\(x=2\)のときに最大値になるとわかります。
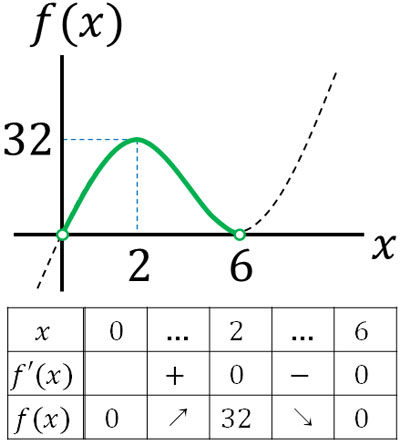
なお\(f(2)=8-48+72=32\)であり、\(y=log_332\)のときに最大値になるとわかります。
\(y=log_332\)
\(y=log_32^5\)
\(y=5log_32\)
こうして\(x=2\)のとき、最大値は\(5log_32\)になります。
対数関数の最大値や最小値の問題を解くとき、\(x\)の範囲を調べるようにしましょう。その後、三次関数を微分することによって最大値や最小値を得られるようになります。
微分を利用して最大値と最長値を見つける
二次関数であれば、微分を利用しなくても最大値と最小値を見つけることができます。一方で三次関数の場合、極大値と極小値があります。そこで微分することによって、極値を見つけましょう。
その後、極大値や極小値、左端、右端の値を比べることによって、どこが最大値や最小値になるのか確認しましょう。これによって、最大値と最小値を求めることができます。
なお三角関数や指数関数、対数関数では問題の解き方が複雑になります。文字の置き換えをしたり、真数条件を利用したりして、三次関数の微分をするのです。これによって\(x\)の範囲や最大値、最小値がわかります。
三次関数の最大値と最小値を求める問題では、微分を利用すると便利です。極値を求めることによって、最大値と最小値がどこなのか確認しましょう。






