数学で学ぶ内容に合同式(mod)があります。高校数学の中でも応用編であり、整数の割り算で重要となる内容が合同式です。整数の割り算について商と余りを数式で表すとき、合同式を利用すれば便利です。
特に証明問題で合同式は非常に優れています。合同式を利用することによって、簡単に証明問題を解くことができるからです。
それでは、合同式を利用してどのように計算すればいいのでしょうか。また、合同式の特徴には何があるのでしょうか。
整数の計算は数学で重要な内容の一つです。そこで合同式を利用し、計算や証明を行えるようになりましょう。
もくじ
合同式(mod)とは、割り算の余りで利用される等式
まず、合同式(mod)とは何でしょうか。整数の割り算について、商と余りを利用して数式で表すとき、以下のように表記します。
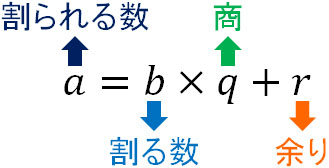
ただ、\(a=bq+r\)を利用して計算すると、計算過程が煩雑になりやすいです。そこで、余りだけに着目した式が開発されました。それが合同式であり、合同式とは「割り算の余りに焦点を当てた式」と理解しましょう。
例えば\(9=4×2+1\)であり、\(13=4×3+1\)です。つまり9と13を比較するとき、4で割ると両方とも余りは1です。そのため、合同式を利用すると以下のように表すことができます。
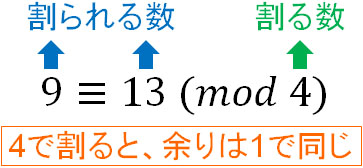
合同式では2つの記号を利用します。それが合同(≡)とmod(余り:modulo)です。以下が合同式の例です。
- \(5≡15\) \((mod\) \(5)\)
- \(13≡1\) \((mod\) \(3)\)
- \(15≡-1\) \((mod\) \(4)\)
- \(-3≡-11\) \((mod\) \(4)\)
なお\(a\)と\(b\)について、\(n\)で割る場合、以下のように表現します。
- \(a≡b\) \((mod\) \(n)\)
このとき、割る数\(n\)を「法」といいます。また余りが等しい場合、複数の合同式をつなげても問題ありません。
\(4≡7≡10\) \((mod\) \(3)\)
合同式を学ぶとき、まずは合同式の特有の数式の意味を覚えるようにしましょう。
合同式の作り方:マイナスを含む合同式
ただ、合同式を作るのは複雑です。特にマイナスを含む合同式では、どのように計算すればいいのかわかりません。そこで、\(a-b\)を利用しましょう。
\(a\)と\(b\)を\(n\)で割るとき、余りが等しいというのは、\(a-b\)が\(n\)の倍数になるのと意味が同じです。合同式を作るとき、\(a-b\)を計算することで\(n\)の倍数になっているかどうかを確認すると効率的です。
この考え方を利用すれば、マイナスを含む場合であっても合同式を作れます。例えば\(-3≡-11\) \((mod\) \(4)\)の場合、\(-3-(-11)=8\)となり、4の倍数であるとわかります。ヒントなしにマイナスを含む合同式を作るのは難しいため、\(a-b\)を計算することで\(n\)倍になっているかどうかを確認しましょう。
なぜ\(a-b\)が有効かというと、余りが同じだからです。余りが同じ場合、\(a-b\)によって余りが消えます。これはつまり、\(n\)の倍数になることと意味が同じです。合同式にマイナスが含まれるケースに限らず、合同式で\(a-b\)を利用するのは役に立つのです。
合同式で利用される性質
なお、合同式で利用される主な性質があり、これを覚えるようにしましょう。合同式には以下の性質があります。
- 合同式を利用して足し算、引き算、かけ算をすることができる
- 互いに素の場合、合同式を利用して割り算ができる
- べき乗数では、合同式に指数を加えても余りは同じ
それぞれの内容を確認しましょう。
合同式での足し算、引き算、かけ算
2つの合同式について、足し算や引き算、かけ算をするとき、余りはどのように変化するのでしょうか。まず、以下の2つの合同式を考えましょう。
- \(8≡11\) \((mod\) \(3)\)
- \(4≡7\) \((mod\) \(3)\)
\(8≡11\) \((mod\) \(3)\)は余りが2です。\(4≡7\) \((mod\) \(3)\)は余りが1です。いずれにしても、このような合同式を作れます。
・合同式の足し算
割る数(今回は3)が同じ場合、合同(≡)で結ばれた数字を足すことができます。そのため、以下のようになります。
\(8+4≡11+7\) \((mod\) \(3)\)
\(12≡18\) \((mod\) \(3)\)
\(12≡18\) \((mod\) \(3)\)の余りは0であり、合同式を満たしているとわかります。
・合同式の引き算
次に引き算を確認しましょう。割る数\(n\)が同じ場合、以下のように引き算をすることができます。
\(8-4≡11-7\) \((mod\) \(3)\)
\(4≡4\) \((mod\) \(3)\)
両方とも余りは1のため、合同式は成り立ちます。
・合同式のかけ算
かけ算についても同様に、割る数\(n\)が同じ場合は以下のようにかけ算をすることができます。
\(8×4≡11×7\) \((mod\) \(3)\)
\(32≡77\) \((mod\) \(3)\)
余りの数は両方とも2になるため、合同式が成り立っています。
・足し算、引き算、かけ算で合同式を利用する
そこで、数式を利用して合同式の性質を表しましょう。以下の2つの合同式があるとします。
- \(a≡b\) \((mod\) \(n)\)
- \(c≡d\) \((mod\) \(n)\)
\(n\)で割るとき、\(a\)と\(b\)の余りは同じです。また、\(n\)で割るとき、\(c\)と\(d\)の余りは同じです。
\(a≡b\) \((mod\) \(n)\)と\(c≡d\) \((mod\) \(n)\)を比較すると、余りの数は異なるかもしれません。ただいずれにしても、\(n\)を利用することで上記の合同式が成り立ちます。このとき、以下のように足し算や引き算、かけ算をすることができます。
- \(a+c≡b+d\) \((mod\) \(n)\)
- \(a-c≡b-d\) \((mod\) \(n)\)
- \(ac≡bd\) \((mod\) \(n)\)
この関係が成り立つため、合同式では自由に移項したり、両辺を等倍したりすることが可能です。合同式を利用するとき、この性質が重要になります。
・練習問題
それでは、\(x\)が最小の自然数となる場合、以下の問題について\(x\)は何でしょうか。
- \(x-4≡7\) \((mod\) \(3)\)
前述の通り、合同式では自由に移項したり、両辺をかけたりできます。そこで、以下のように移項しましょう。
\(x-4≡7\) \((mod\) \(3)\)
\(x≡7+4\) \((mod\) \(3)\)
\(x≡11\) \((mod\) \(3)\)
ただ、\(x\)は最小の自然数です。そこで、以下のように変形しましょう。
\(x≡11≡2\) \((mod\) \(3)\)
こうして、\(x=2\)が正解です。
合同式の割り算は互いの素の場合のみ可能
それでは、合同式の割り算はどう考えればいいのでしょうか。先ほどとは異なり、両辺を自由に割ってはいけません。わり算をするとき、以下の\(a\)と\(n\)が互いに素の場合のみ可能です。

例えば、以下の合同式を考えてみましょう。
- \(14≡8\) \((mod\) \(3)\)
この合同式について、2で割りましょう。2と3(mod)は互いに素であるため、割り算することができます。この場合、以下のように変化します。
\(14÷2≡8÷2\) \((mod\) \(3)\)
\(7≡4\) \((mod\) \(3)\)
こうして、余りが1になる合同式を作ることができました。一方、以下の合同式を考えてみましょう。
- \(14≡10\) \((mod\) \(4)\)
この合同式について2で割りましょう。2と4は互いに素ではありません。すると、以下のようになります。
\(14÷2≡10÷2\) \((mod\) \(4)\)
\(7≡5\) \((mod\) \(4)\)(合同式が成立しない)
7を4で割ると、余りは3です。一方、5を4で割ると余りは1です。こうして、合同式が成立しません。合同式を利用して割り算をするためには、互いに素の関係を利用しなければいけません。
・練習問題
それでは\(x\)が最小の自然数となる場合、以下の問題について\(x\)は何でしょうか。
- \(3x≡13\) \((mod\) \(5)\)
\(a-b\)が5の倍数になればいいため、以下の式を作りましょう。
\(3x-13=5\)
\(3x=18\)
つまり、以下の式へ変形できます。
\(3x≡18\) \((mod\) \(5)\)
\(3x≡3×6\) \((mod\) \(5)\)
3と5は互いに素なので、割り算をすることができます。つまり、以下の式になります。
\(x≡6\) \((mod\) \(5)\)
ただ\(x\)は最小の自然数なので、以下の合同式を作りましょう。
\(x≡6≡1\) \((mod\) \(5)\)
法が5であるため、5の倍数を利用して引き算(または足し算)をすることができます。そこで\(6-5=1\)になり、\(x=1\)が答えであるとわかります。
べき乗(累乗)での合同式の計算方法
次にべき乗(累乗)での合同式を確認しましょう。指数を含む合同式では、どのように計算すればいいのでしょうか。例えば、以下の合同式があるとします。
- \(4≡7\) \((mod\) \(3)\)
そこで、以下のように二乗や三乗をしてみましょう。
・二乗を行う
\(4^2≡7^2\) \((mod\) \(3)\)
\(16≡49\) \((mod\) \(3)\)
・三乗を行う
\(4^3≡7^3\) \((mod\) \(3)\)
\(64≡343\) \((mod\) \(3)\)
このように確認すると、\(a-b\)によって3の倍数を作れます。つまり指数を含む合同式について、累乗をしても余りは変化しません。そのため、以下の関係が成り立ちます。
![]()
このように共通する指数を利用すれば、合同式では指数を取り外すことができます。
・練習問題:べき乗での余りを求める
それでは\(x\)が最小の自然数となる場合、以下の問題の答えは何でしょうか。
- \(13^{100}\)を4で割ったときの余りを求めましょう。
13の100乗を計算してはいけません。そうではなく、以下の合同式を作ることを考えましょう。
\(13^{100}≡b^{100}\) \((mod\) \(4)\)
この合同式を作れば、100乗を取り外すことができます。その結果、余りの計算が楽になります。
100乗を取り外して\(13≡b\) \((mod\) \(4)\)を作るとき、\(13-b\)が4の倍数になればいいです。そこで4の倍数である12を利用し、\(13-12=1\)によって以下の式を作りましょう。
\(13≡1\) \((mod\) \(4)\)
累乗を含む合同式の計算問題では、合同式に含まれる値(今回の例では\(b\))が最も小さい自然数となるように設定し、新たな合同式を作りましょう。そうすれば、計算が簡単になります。先ほどの式では、最も小さい自然数は1なので\(13≡1\) \((mod\) \(4)\)とします。
次に、両辺を100乗しましょう。
\(13^{100}≡1^{100}\) \((mod\) \(4)\)
重要なのは、\(1^{100}=1\)であることです。そのため、以下の合同式を作れます。
\(13^{100}≡1^{100}≡1\) \((mod\) \(4)\)
1に着目すると、4で割るときの余りは1です。つまり、\(13^{100}\)を4で割ったときの余りは1です。
・練習問題:1の位を求める
なお合同式の計算では、1の位を求めなければいけないケースもあります。自然数の1の位を求めるというのは、10で割るときの余りを出すのと意味が同じです。例えば23を10でわると、余りは3です。736を10でわると、余りは6です。このように、10で割れば1の位を得ることができます。
それでは、以下の問題の答えは何でしょうか。
- \(13^{101}\)について、1の位を求めましょう。
まず、合同式を作りましょう。法は10なので、以下の合同式を作れます。
\(13≡3\) \((mod\) \(10)\)
つまり、\(13^{101}≡3^{101}\) \((mod\) \(10)\)を作ればいいとわかります。そこで3に着目して、指数を含む以下の合同式を作りましょう。
- \(3^2≡9\) \((mod\) \(10)\)
- \(3^3≡27≡7\) \((mod\) \(10)\)
- \(3^4≡81≡1\) \((mod\) \(10)\)
べき乗の計算により、\(3^4≡1\) \((mod\) \(10)\)の合同式を発見したため、これを利用することで問題を解きましょう。以下のようになります。
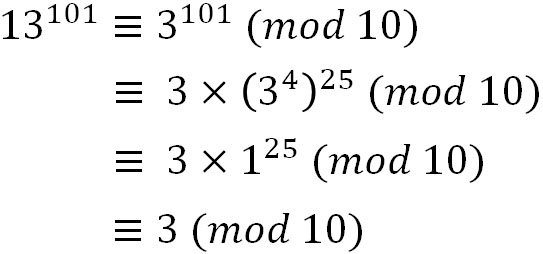
そこで3に着目すると、3を10で割るときの余りは3です。そのため、\(13^{101}\)の1の位は3とわかります。
整数の割り算で数式の代わりに合同式を使って証明する
それでは、なぜ合同式を学ぶ必要があるのでしょうか。合同式を利用する場合、割り算での余りや倍数が関わる問題を解くのが非常に簡単になります。複雑な計算をしなくても、整数の割り算や倍数の証明問題を解くことができるのです。
整数の割り算や倍数の証明問題では、以下の数式を利用することによって問題を解きます。
- \(a=bq+r\)
ただ、特に累乗を含む式では計算が大変です。そこで合同式を利用すれば、面倒な計算なしに整数の割り算や倍数の証明問題を解けるようになります。
例として、以下の証明問題を解いてみましょう。
- \(n^4+2n^2\)が3の倍数であることを証明しましょう。
ここでは合同式を利用して証明しましょう。まず、3の倍数なので余りは0になります。そのためすべての整数について、\(n^4+2n^2\)の余りが0であると証明すればいいです。
また倍数のように法が固定される場合、余りは法を基準にした規則性があります。例えば3の倍数(法が3)の場合、以下のように3が加わるごとに余りが同じになります。
- \(1≡4≡7\) \((mod\) \(3)\):余り1
- \(2≡5≡8\) \((mod\) \(3)\):余り2
- \(3≡6≡9\) \((mod\) \(3)\):余り0
法則性があることについては、合同式を作るときに「\(a-b\)が3の倍数になるかどうか」を調べればいいことからもわかります。つまり\(n^4+2n^2\)が3の倍数かどうか調べるためには、任意の整数\(k\)について、以下のケースの余りがどのようになるのか調べればいいとわかります。
- \(k\) \((mod\) \(3)\)
- \(k+1\) \((mod\) \(3)\)
- \(k+2\) \((mod\) \(3)\)
\(k\)はどの値であっても問題ありません。計算しやすい値を利用することで証明しましょう。そこで、\(k=1\)のときの余りを調べましょう。つまり\(n\)が1または2または3のとき、余りを調べます。
・\(n=1\)のとき
\(n^4\)を調べましょう。\(1^4=1\)であり、\(1\) \((mod\) \(3)\)の余りは1です。次に\(2n^2\)を調べましょう。\(2×1^2=2\)であり、\(2\) \((mod\) \(3)\)の余りは2です。そのため\(n^4+2n^2\)の余りは0になります。
・\(n=2\)のとき
\(n^4\)について、\(2^4=16\)であり、\(16\) \((mod\) \(3)\)の余りは1です。また\(2n^2\)について、\(2×2^2=8\)です。\(8\) \((mod\) \(3)\)の余りは2です。そのため\(n^4+2n^2\)の余りは0になります。
・\(n=3\)のとき
\(n^4\)に3を代入すると、\(3^4=81\)となり、\(81\) \((mod\) \(3)\)の余りは0です。\(2n^2\)については、\(2×3^2=18\)となり、\(18\) \((mod\) \(3)\)の余りは0です。そのため\(n^4+2n^2\)の余りは0になります。
3の倍数では、すべての整数を\(k\)、\(k+1\)、\(k+2\)で表すことができます。また前述の通り、法ごと(今回は3の倍数なので3ごと)に同じ余りが繰り返されます。ただ今回の計算より、すべてのケースで余りが0であるため、以下の合同式を作れます。
\(n^4+2n^2≡3\) \((mod\) \(3)\):余り0
こうして、\(n^4+2n^2\)は3の倍数であると証明できました。
法よりも小さい数に着目して証明する
ここまで解説したポイントからわかる通り、証明問題で合同式を利用する場合は法よりも小さい数に着目しましょう。例えば法が8なのであれば、1~7の数字を利用します。また法が10であり、奇数の整数を対象に計算したいのであれば、1, 3, 5, 7, 9について調べます。
例えば、以下の問題があるとします。
- \(n\)が奇数のとき、\(n^2-1\)は8の倍数であることを証明しましょう。
この場合、8の倍数なので1~7に着目しましょう。ただ奇数が対象であるため、1, 3, 5, 7について\(n^2-1\)の余りを調べます。そうすると、以下のようになります。
・\(n=1\)のとき
\(1^2-1=0\)であるため、8で割るときの余りは0です。
・\(n=3\)のとき
\(3^2-1=8\)であるため、8で割るときの余りは0です。
・\(n=5\)のとき
\(5^2-1=24\)であるため、8で割るときの余りは0です。
・\(n=7\)のとき
\(7^2-1=48\)であるため、8で割るときの余りは0です。
結果より、以下の合同式を作れます。
\(n^2-1≡8\) \((mod\) \(8)\):余り0
合同式を利用して証明する場合、余りに規則性があることに着目しましょう。そこで法よりも小さい数を利用し、余りが0であることを計算できれば、特定の値の倍数であると証明できます。また合同式を利用すれば、割り算をするときの余りを確認できます。
合同式を利用して割り算の余りや倍数を確認する
整数の割り算について、商と余りを利用して計算するとき、\(a=bq+r\)の式を利用します。ただ数式を利用して余りを計算する場合、計算過程が大変です。
そこで合同式を利用しましょう。わり算をするときに余りに着目するのが合同式です。そのため合同式を利用すれば、割り算での余りや倍数の計算が楽になります。
特に証明問題を解く場合、合同式を利用すると計算時間を大幅に短縮でき、計算ミスを少なくできます。合同式を利用する場合、たとえ指数を含む式であったとしても、簡単な計算に変えることができます。
整数の計算をするとき、合同式は有用です。特に割り算や倍数の計算をするとき、合同式を利用してみましょう。






